Элементы-алгебры-Шайкин-А.Н

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский химико-технологический университет им. Д.И. Менделеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ax By Cz D 0,

..pdf

Скачиваний:

554

Добавлен:

12.03.2016

Размер:

1.95 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

г) x 2y 2z 7 0, x y 35 0.

Задача 14. Найти абсциссу точки А, равноудаленной от точек B и C:

а) A(x;0;0),B(1;5;9),C(3;7;11); б) A(x;0;0),B(4;6;8),C(2;4;6);

в) A(x;0;0),B(1;2;3),C(2;6;10);

г) A(x;0;0),B( 2; 4; 6),C( 1; 2; 3).

Задача 15. Исследовать на линейную зависимость систему векторов:

а) a (1;2;3),b (6;5;9),c (7;8;9); б) a (2;1;0),b ( 5;0;3),c (3;4;3);

в) a (2;0;2),b (1; 1;0),c (0; 1; 2);

г) a ( 2;1;5),b (4; 3;0),c (0; 1;10).

1.7. Ответы

1. а) 1; б)

0; в) 1; г)

0. 2. а) 1; б) 6;1; в)

2 k,k Z ; г) 64;0,5. 3. а) 40;

б) 21; в) 0; г)

1. 4. а) 0,6; б) 1; 14/9; в) Если a 0, то

x R, если a 0, то

x a;

г) Если ab bc ac 0 и

abc 0, то

x R, если

ab bc ac 0

abc 0,

то x ,

если ab bc ac 0,

то

abc

а)

ab bc ac

x 2p 4q 3r ; б) x 4p 3q r ; в) x 4p 2q r ; г)

x 8p 13q 3r . 6.

а) да; б) нет; в) да; г)

да. 7. а) 135o ; б) 60o ; в) 0o ; г) 180o . 8. а) 31;

б) 7

; в)

102; г)

9. а) нет; б) да; в)

нет; г) да. 10. а)

V 70/3; h 140/

;

1021

б) V 191/ 6; h 191/

;

в)

V 73; h 146/

;

г)

V 6; h 3

573

11. а) 49/ (3

б)

40/

;

в)

;

г)

35/

21);

737

12. а) (

;

); б) (

;

);

в) (

;

);

г)

206

178

(

;

). 13. а) 30o ; б) 45o ; в) 60o ; г) 45o . 14. а) 18; б) 15; в)

851

63; г) 21. 15. а) линейно независимы; б) линейно зависимы; в) линейно независимы; г) линейно зависимы.

2.ЛИНИИИПОВЕРХНОСТИ

2.1.Прямаяна плоскости

Теорема. Прямая, проходящая через точку M0 x0,y0 под		углом к
положительному направлению оси	OX ( 90o ) имеет	уравнение
y y0 k(x x0), где k tg – угловой коэффициент.

Доказательство.	Пусть
М x,y – произвольная	точка

прямой (рис. 2). Рассмотрим

случай		0o 90o				(другой
случай				рассматривается
аналогично).			Так как			прямые
(N,M0 ) и (ОХ) параллельны, то
MM0N .						Тогда
k tg		MN		y y

				0	.

	M0N
				x x0
Следовательно,				y y0 k(x x0).

у М

М0

у0 N

х0

Рис. 2

Следствие. Если M0 OY , т. е. M0(0,b), то уравнение прямой, проходящей через эту точку под углом к положительному направлению оси OX ( 90o ) имеет уравнение y k x b, где k tg – угловой коэффициент.

Доказательство. Подставим в выведенное уравнение прямой координаты

точки M0 :

y b k(x 0). Тогда

y k x b.

Замечание. Если 90o ,

то уравнение прямой, проходящей через точку

M0 x0,y0 , очевидно, имеет вид

x x0 .

Замечание. Уравнение

y y0

k(x x0) с параметром

является

уравнением пучка прямых, проходящих через точку M0 , кроме прямой x x0 .

Определение. Уравнение

1 называется

уравнением

прямой в

отрезках. Эта прямая пересекает оси координат в точках (a;0) и (0;b).

Теорема. Прямая, проходящая через две точки

M1 x1,y1

M2 x2,y2

(x x ,

x ) имеет уравнение

x x1

y y1

x2 x1

y2 y1

Доказательство. Пусть M x,y

– произвольная точка прямой (рис. 3).

Рассмотрим случай 0o 90o (другой случай рассматривается аналогично).

Легко видеть, что M1MP ~

M1M2N

(по

двум углам). Тогда

M1P

т. е.

M1N

M2N

x x1

y y1

у2

М2

x2 x1

y2 y1

М1

Теорема.

Уравнение

вида у1

Ax By C 0,

где

B2 0,

есть

уравнение прямой, и обратно,

любая

прямая может быть задана уравнением

х1 х2

х х

такого вида.

Пусть

дано

Рис. 3

Доказательство.

уравнение Ax By C 0,

и пусть B 0. Тогда это уравнение можно привести

к виду

т. е.

к виду

y k x b, про который доказано,

что он

M0(0,b)

задает прямую, пересекающую ось OY в точке

и проходящую под

углом ( 90o ) к положительному направлению оси

OX . Если В = 0, то

A 0. Тогда уравнение можно привести к виду x C / A,

то есть к виду x x0

уравнения прямой, пересекающей ось OХ в точке M0(x0,0) и проходящей под

углом 90o	к положительному направлению оси OX . Обратно, пусть есть
невертикальная	прямая. Тогда она имеет уравнение вида y k x b. Это

уравнение можно привести к виду k x y b 0, т.

е. к видуAx By C 0.

Если прямая вертикальная, то ее

уравнение x x0

можно привести к виду

x 0 y x0

0, т. е. к видуAx By C 0.

Теорема.

Пусть

есть

две

прямые,

уравнения

которых

y k1 x b1

y k2 x b2 . Тогда

угол между ними (острый) можно

получить

из

формулы

k2 k1

1 k1

Доказательство.

Так

как

внешний

угол

(рис.

треугольника

равен

сумме

двух

углов треугольника, не смежных с

ним,

то

или

Рис. 4

1. Если

– острый, то

tg tg 0. Если

– тупой,

то tg tg tg

(tg 0). Тогда по

определению модуля, по формуле разности тангенсов и определению k1 и k2

имеем tg |tg |=

tg 2 tg 1

k2 k1

1 tg 1 tg 2

1 k1 k2

Следствие. Пусть есть две прямые,

уравнения которых y k1 x b1 и

y k

x b .

Тогда они параллельны,

т.

е.

tg 0,

если

k2 k1

1 k1 k2

т. е.

и перпендикулярны,

т.

е.

90o ,

tg не

существует,

если

1 k1 k2 0,

т. е. k1 k2 1.

2.2.Прямаяи плоскость впространстве

Утверждения и формулы данного раздела являются следствиями тех фактов, что были получены в векторной алгебре. Поэтому их доказательства не приводятся.

Уравнение плоскости, проходящей через точку перпендикулярно вектору

Каждую плоскость в пространстве можно представить как линейное уравнение, называемое общим уравнением плоскости Ax By Cz D 0, где

A2 B2 C2 0. Коэффициенты A, B, C являются координатами вектора n (A;B;C), нормального (т. е. перпендикулярного) к плоскости.

Если в общем уравнении плоскости D 0, то плоскость проходит через

начало координат. При A 0 (B 0,	C 0) плоскость параллельна оси OX
(оси OY , оси OZ ) соответственно.	При A B 0 (A C 0, B C 0)

плоскость параллельна плоскости (x,y) (плоскости (x,z), плоскости (y,z)).

Дана точка M(x0;y0;z0) и вектор n (A;B;C). Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору, имеет вид:

A(x x0) B(y y0) C(z z0) 0.

Дана прямая	как	пересечение плоскостей Ax B y C z D 0 и
A2x B2 y C2z D2	0.	1	1	1	1
		Уравнение любой плоскости,	проходящей через

данную прямую, имеет вид:

(Ax1 B1y C1z D1) (A2x B2 y C2z D2) 0,

где и – некоторые действительные числа.

Уравнение плоскости, проходящей через три точки

Через три данные точки M1(x1;y1;z1), M2(x2;y2;z2), M3(x3;y3;z3) проходит только одна плоскость, уравнение которой получается из условия компланарности радиус-векторов точек плоскости

x x1	y y1	z z1
x2 x1	y2 y1	z2 z1	0,
x3 x1	y3 y1	z3 z1

для этого необходимо вычислить определитель и привести полученное уравнение к общему виду.

Нормальное уравнение плоскости

В векторной

форме

уравнение

плоскости имеет

вид r n D 0,

r x,y,z . Если нормальный вектор плоскости – единичный, т. е.

;

A2 B2 C2

то уравнение плоскости можно записать в виде

xcos ycos zcos p 0 (нормальное уравнение плоскости),

где p – расстояние от начала координат до плоскости, cos , cos , cos –

направляющие косинусы нормали

cos

, cos

A2 B2 C2

где , , – углы между нормалью плоскости и осями координат OX , OY , OZ соответственно.

Общее уравнение плоскости может быть приведено к нормальному виду

1
умножением на нормирующий множитель			.

	A2 B2 C2
Расстояние от точки M0 x0,y0,z0 до плоскости		Ax By Cz D 0

находится по формуле, полученной подстановкой точки в нормальное уравнение

d Ax0 By0 Cz0 D .

A2 B2 C2

Уравнение плоскости в отрезках

Если в общем уравнении D 0, то, разделив на D, приведем уравнение плоскости к виду в отрезках

x y z 1, a b c

где a D , b D, c D определяют соответственно абсциссу, ординату и

A B C

аппликату точек пересечения плоскости с осью OX – a,0,0 , осью OY –

0,b,0 , осью OZ – 0,0,c .

	Угол между плоскостями
Угол	между двумя плоскостями Ax B y C z D 0 и
	1	1	1	1

A2x B2 y C2z D2 0

находят как угол между их нормальными векторами

n1 A1,B1,C1 и n2 A2,B2,C2 :

cos

| AA BB CC

Плоскости параллельны,

когда их

нормали

коллинеарны, т. е.

A1 / A2 B1 / B2 C1 /C2 .

Плоскости

перпендикулярны,

когда их нормали

перпендикулярны, т. е. n1 n2 AA1 2 BB1 2 CC1 2 0.

Прямая в пространстве

Уравнения

прямой,

проходящей

через

две точки

M1 x1,y1,z1 и

x ,y ,z

имеют вид

x x1

y y1

z z1

y2 y1

z2 z1

M1 x1,y1,z1

Уравнения

прямой,

проходящей

через

данную

точку

параллельно

данному

направляющему

вектору

s (l,m,n)

–

канонические

уравнения прямой

x x1

y y1

z z1

Вводя параметр t,

x x1

y y1

z z1

t , получаем параметрический

вид уравнений прямой

x lt x1

y mt y1 .

z nt z

Каждая прямая в пространстве может быть представлена системой двух

уравнений (задана как пересечение двух плоскостей)

Ax B y C z D 0

A2x B2 y C2z D2 0

Угол между двумя прямыми

Прямые

заданы

каноническом

виде

x x1

y y1

z z1

x x2 y y2 z z2 . Угол между прямыми определяется как угол между l2 m2 n2

их направляющими векторами s1 (l1,m1,n1), s2 (l2,m2,n2)

|s s |

|ll mm nn |

1 2

cos

l 2

2 m

n 2

Очевидны

условия

параллельности

l1 /l2 m1 / m2 n1 / n2 ,

перпендикулярности прямых l1l2 m1m2 n1n2 0.

Пересечение прямой и плоскости

Угол

между прямой и плоскостью определяют через угол

между

направляющим вектором

прямой

s (l,m,n)

нормалью

плоскости

N (A,B,C):

Al Bm Cn|

sin sin(90 ) cos

A2 B2 C2

l2 m2 n2

Прямая и плоскость параллельны, если направляющий вектор

прямой

ортогонален нормальному вектору плоскости N ,

т. е. Al+Bm+Cn=0. Прямая

и плоскость

взаимно перпендикулярны,

если

направляющий вектор

s и

нормаль N параллельны A/l B / m C / n.

Если Al Bm Cn 0, то прямая и плоскость имеют единственную точку пересечения, определить которую можно из системы

Удобно использовать параметрический вид уравнений прямой

Ax By Cz D 0,

	x lt x1,

	y mt y1,

	z nt z1.

Решением системы будет значение параметра t t0,при котором прямая и плоскость пересекутся. По значению параметра находят соответствующие x0,y0,z0 координаты точки пересечения.

2.3.Кривыевторого порядка

Окружность

Определение. Окружностью называется геометрическое место точек на плоскости, равноудаленных от некоторой точки, называемой центром. Расстояние от точек окружности до центра называется радиусом.

Теорема. Если точка M(x,y) принадлежит окружности с центром в начале координат и радиуса r, то ее координаты удовлетворяют уравнению x2 y2 r2 , и обратно.

Доказательство легко следует из теоремы Пифагора.

Определение. Уравнение x2 y2 r2 называется каноническим уравнением окружности.

Эллипс

Определение. Эллипсом называется геометрическое место точек на плоскости, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2а, большее, чем расстояние 2с между фокусами.

Теорема. Если точка M(x,y) принадлежит эллипсу с фокусами в точках

F1( c,0)

F2(c,0)

и сумма расстояний от нее до фокусов равна 2а, то ее

координаты удовлетворяют уравнению

где b

, и обратно.

(Уравнение

1 называется каноническим уравнением эллипса.)

Доказательство. По определению эллипса имеем: |MF1 | |MF2 | 2a, т. е.

x c 2

x c 2 y2

2a. Перенося один радикал в правую часть, и

возводя обе части уравнения в квадрат, получаем:

x c 2 y2

x2 2xc c2 y2 4a2 4a

x c 2 y2

x2 2xc c2 y2 ,

x c 2

4a2 4xc.

Еще раз возводя обе части уравнения в квадрат,

получаем: a2x2 2a2xc a2c2

a2 y2 a4 2a2xc x2c2 ,

x2 c2 y2

x2c2

a2 c2

y2 a2 c2 .

Учитывая,

что

b2 a2 c2 ,

имеем:

x2 y2 b2 ,

т.

е.

Обратно,

пусть точка

M(x,y)

удовлетворяет

уравнению

Докажем,

что

MF MF 2a.

Действительно, MF MF =

x c 2

x c 2 b2(1

)

x c 2 b2(1

) =

2xc

b2x

2xc c

b2x2

= 1

2xc c

2xc

a2 b2

2xc c

cx 2

2xc a

cx			2
		a	=
	a

=2а, поскольку

a и c a.

Определение.

Эксцентриситетом эллипса называется отношение

фокального расстояния c к большой полуоси a, т. е. e c . Легко видеть, что a

e [0;1).

Замечание. Если фокусы находятся на оси OY , то b a.

Гипербола

Определение. Гиперболой называется геометрическое место точек на плоскости, для каждой из которых модуль разности расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2а, меньшее, чем расстояние 2с между фокусами.

Теорема. Если точка M(x,y) принадлежит гиперболе с фокусами в

точках

F1( c,0)

F2(c,0) и модуль разности расстояний от нее до фокусов

равен

2а,

то

ее

координаты

удовлетворяют

уравнению

где

b2 c2

a2 , и

обратно.

(Уравнение

1 называется

каноническим

уравнением гиперболы.)

Доказательство. По определению гиперболы имеем: |MF1 MF2 | 2a,

т.е.

x c 2 y2

x c 2

| 2a.

Тогда

получается,

что

x c 2 y2 x c 2 y2 2a. Перенося один радикал в правую часть, и

возводя обе части уравнения в квадрат, получаем:

x c 2 y2 2a x c 2 y2 ,

x2 2xc c2 y2 4a2 4а x c 2 y2 x2 2xc c2 y2 ,

4a x c 2 y2 4xc 4a2 . Еще раз возводя обе части уравнения в квадрат,

получаем:	a2x2 2a2xc a2c2 a2 y2 a4 2a2xc x2c2 ,
x2 c2 y2	a2	x2c2	,	a2 c2	x2 y2 a2 c2 . Учитывая, что	b2 с2 а2 ,
		a2		a2

имеем:

x2 y2 b2 , т. е.

1. Обратно,

пусть точка

M(x,y)

удовлетворяет

уравнению

Докажем,

что

|MF MF | 2a.

Действительно, MF MF =

x c 2 y2

x c 2

y2 =

x c 2 b2(

1) =

2xc

b2x

2xc

b2x2

2xc

a2 b2

2xc

2xc a

cx 2

2xc a

cx			2
		a	=
	a

a 2a

(x a)

a 2a

(x a)

Т. е. MF1 MF2 = 2а. Следовательно

|MF1 MF2 | 2a.

Определение.

Эксцентриситетом

гиперболы

называется отношение

фокального расстояния c к действительной полуоси a, т. е. e с . Легко видеть,

что e (1; ).

Замечание. Если фокусы находятся на оси OY , то каноническое

уравнение будет

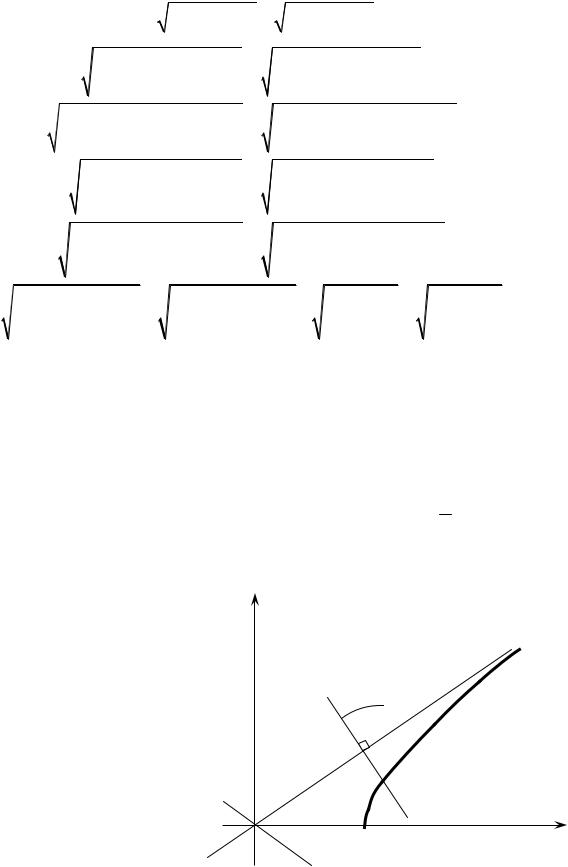
Теорема.

Гипербола,

уравнение

которой

имеет асимптоты y

Доказательство.

Покажем,

что

lim

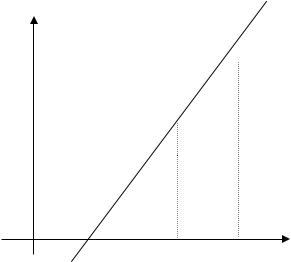
Действительно (рис. 5),

Рис. 5

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.09.20194.78 Mб3Экзаменационный билет N 19.doc
#
13.02.2015125.44 Кб24Экология курсовая.doc
#
13.02.201529 Кб16экология.docx
#
13.02.2015133.04 Кб8ЭКОНОМ ЗАЧЕТ.docx
#
15.04.2019591.87 Кб0экономика_7 задание.doc
#
12.03.20161.95 Mб554Элементы-алгебры-Шайкин-А.Н..pdf
#
23.11.2019144.38 Кб51Эпоксидные смолы.doc
#
13.02.201513.76 Mб51Эффект Комптона.doc
#
26.11.201965.02 Кб1Ювен._право(1).doc
#
27.11.2019155.06 Кб3юююююююююху.docx
#
18.08.2019105.47 Кб6языкознание.doc