
Эффект комптона
Цель работы: наблюдение на компьютерной модели эффекта Комптона, сопровождающего рассеяние рентгеновского излучения веществом, доказательство квантовых свойств коротковолнового электромагнитного излучения (гамма- и рентгеновских лучей) путём исследования спектра его рассеяния.
Теоретическое введение и описание экспе-риментальной (модельной) установки
В случаях, когда волны отражаются или претерпевают дифракцию на препятствиях, нет основания ожидать изменения их длины волны или частоты. Это следует из классической теории Дж.Томсона, в соответствии с которой под действием периодического электрического поля световой волны электроны вещества колеблются с частотой поля и, вследствие этого, излучают вторичные (рассеянные) волны той же частоты. Поэтому немалое удивление вызвал опыт Комптона (1922 г.), показавший, что у рентгеновских лучей, рассеянных атомами, наряду с первоначальной частотой обнаруживается новая частота '. Такое рассеяние со сдвигом частоты (или длины волны ) называется эффектом Комптона. Более строго под эффектом Комптона понимается явление, сопровождающее рассеяние электромагнитного излучения на свободных (слабосвязанных) электронах1 атома, приводящее к изменению его частоты (длины волны). Поскольку величина (или ) весьма мала, эффект Комптона экспериментально наблюдается только для коротковолновых излучений - рентгеновских или гамма-лучей, для которых относительное изменение частоты оказывается существенным. Результаты этого опыта можно объяснить, только предположив, что электромагнитное излучение представляет собой поток частиц – фотонов. Фотоны обладают импульсом, и их взаимодействие с электронами вещества происходит подобно сталкивающимся шарам по законам абсолютно упругого соударения.
За проведенные эксперименты и истолкование их результатов в 1927 г. американский физик Артур Комптон был удостоен Нобелевской премии.
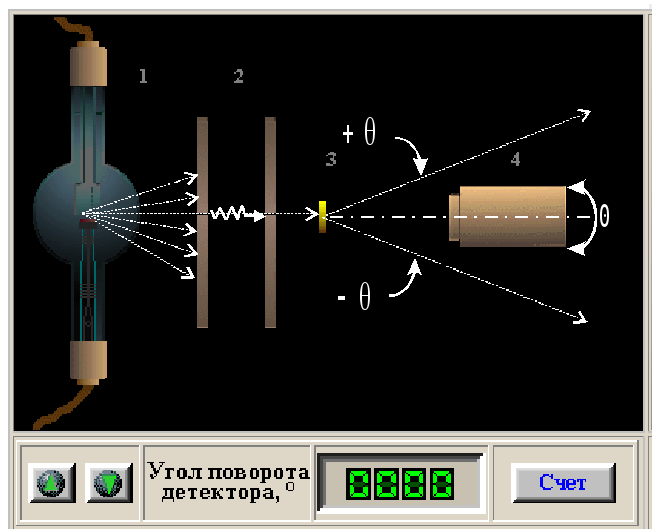
Рис. 1. Схема опыта по изучению эффекта Комптона:
1 – излучатель (рентгеновская трубка); 2 – диафрагмы, выделяющие пучок излучения; 3 – образец исследуемого вещества; 4 – детектор рассеянного под углом излучения
Установка
для
изучения
эффекта
Комптона
(упрощённая схема представлена на рис.
1) состоит
из
рентгеновской
трубки
(1), двух
диафрагм
(2), выделяющих
узкий
пучок
монохроматического
рентгеновского
излучения,
образца - фольги
исследуемого
вещества
(3) и
детектора
излучения
(4). Детектор
рентгеновского излучения представляет
собой фотоэлектронный умножитель (ФЭУ)
с кристаллом NaI(Tl)
(активированным талием). Детектор
чувствителен к квантам излучения
(фотонам), под воздействием которых в
кристалле возникают вспышки света
(сцинтилляции), преобразуемые ФЭУ в
импульсы тока, которые регистрируются
электронным счётчиком (на схеме не
показан). При этом амплитуда токового
импульса оказывается пропорциональной
интенсивности сцинтилляции (яркости
вспышки) и, таким образом, энергии
![]() регистрируемого кванта электромагнитного
излучения (
регистрируемого кванта электромагнитного
излучения (![]() - постоянная Планка). Детектор может
поворачиваться
относительно
оси падающего на образец излучения на
заданный угол
.
Таким образом, в эксперименте осуществляется
угловой энергетический анализ излучения,
рассеянного образцом, т.е. получается
зависимость энергии E
(частоты
или длины волны )
рассеянного излучения от угла рассеяния
.
- постоянная Планка). Детектор может
поворачиваться
относительно
оси падающего на образец излучения на
заданный угол
.
Таким образом, в эксперименте осуществляется
угловой энергетический анализ излучения,
рассеянного образцом, т.е. получается
зависимость энергии E
(частоты
или длины волны )
рассеянного излучения от угла рассеяния
.
Для
получения количественных соотношений
и рабочих формул, связанных с эффектом
Комптона, рассмотрим взаимодействие
падающего на вещество фотона, обладающего
энергией
![]() и импульсом
и импульсом
![]() k
=
k
=
![]() /c
(с
– скорость света),
с
покоящимся электроном, имеющим энергию
покоя m0c2
(m0
– масса покоя электрона). Предположим,
что в результате рассеяния фотона на
электроне импульс и энергия фотона
становятся равными
/c
(с
– скорость света),
с
покоящимся электроном, имеющим энергию
покоя m0c2
(m0
– масса покоя электрона). Предположим,
что в результате рассеяния фотона на
электроне импульс и энергия фотона
становятся равными
![]() k
и
k
и
![]() .
Электрон при этом приобретает импульс
.
Электрон при этом приобретает импульс
![]() и энергию
и энергию![]() =c
=c![]() .
Последняя формула получается из
известного релятивистского соотношения
.
Последняя формула получается из
известного релятивистского соотношения![]() .
Применение релятивистских формул
необходимо, поскольку в эффекте Комптона
энергия рассеянного электрона составляет
величину порядка его энергии покоя.
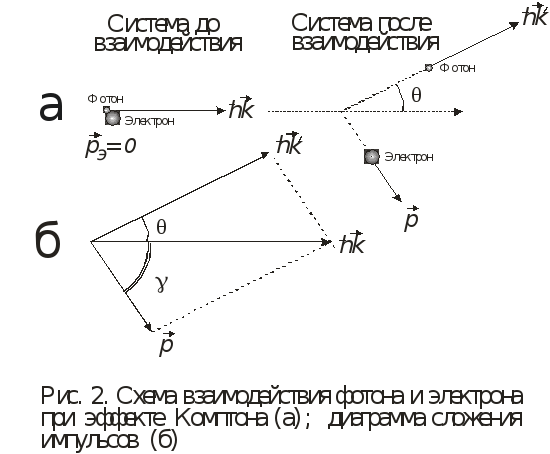
Векторная диаграмма импульсов при
комптоновском рассеянии изображена на
рис. 2. Запишем выражения для законов
сохранения энергии и импульса в системе
фотон-электрон, которую будем считать
изолированной:
.
Применение релятивистских формул
необходимо, поскольку в эффекте Комптона
энергия рассеянного электрона составляет
величину порядка его энергии покоя.
Векторная диаграмма импульсов при
комптоновском рассеянии изображена на
рис. 2. Запишем выражения для законов
сохранения энергии и импульса в системе
фотон-электрон, которую будем считать
изолированной:
![]() +
+
![]() =
=
![]()
+ c
+ c![]() ,
(1)
,
(1)
![]() =
=
![]() +
+
![]() (2)
(2)
Из системы уравнений (1) – (2) после простых, но громоздких преобразований можно получить (см. библиографический список [1]) выражение для частоты рассеянного в эффекте Комптона фотона
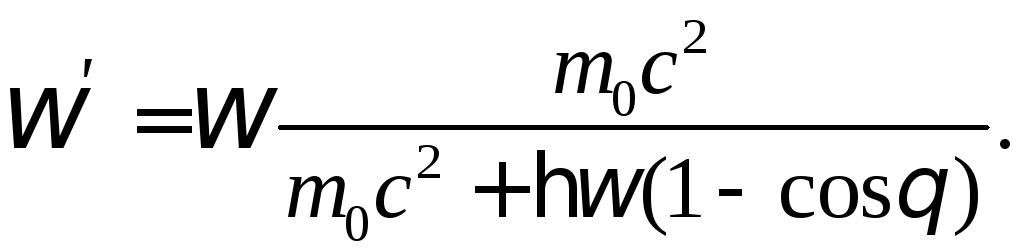 (3)
(3)
Из
формулы (3)
следует, что частота рассеянного
излучения оказывается меньше частоты
излучения, падающего на вещество, для
всех углов, отличных от
= 0 (отсутствие рассеяния). Кроме того,
эта формула подтверждает отсутствие
наблюдаемого эффекта в случае, когда
падающее излучение имеет малую энергию
по сравнению с энергией покоя электрона
![]() (“мягкое” излучение). При этом вторым
слагаемым в знаменателе выражения (3)
можно пренебречь, что даёт
(“мягкое” излучение). При этом вторым
слагаемым в знаменателе выражения (3)
можно пренебречь, что даёт
![]() .
Из формулы (3) можно найти изменение
длины волны при комптоновском рассеянии.
Заменяя
.
Из формулы (3) можно найти изменение
длины волны при комптоновском рассеянии.
Заменяя
![]() по соотношению
по соотношению![]() ,
получим
,
получим
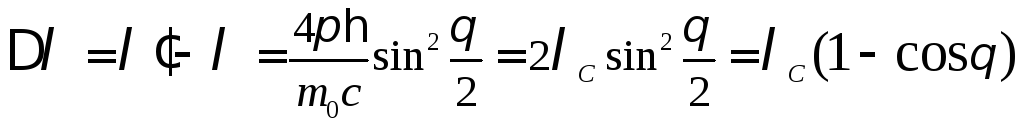 .
(4)
.
(4)
Константу
 называют
комптоновской длиной волны электрона.
называют
комптоновской длиной волны электрона.
Электрон, провзаимодействовавший с фотоном в эффекте Комптона, называется электроном отдачи. Его кинетическая энергия T может быть найдена с использованием соотношениё (1) - (4) получаем
 ,
(5)
,
(5)
где
=
![]() ;E0
– энергия нерассеянного фотона.
;E0
– энергия нерассеянного фотона.
Как
видно из (5), наибольшую кинетическую
энергию
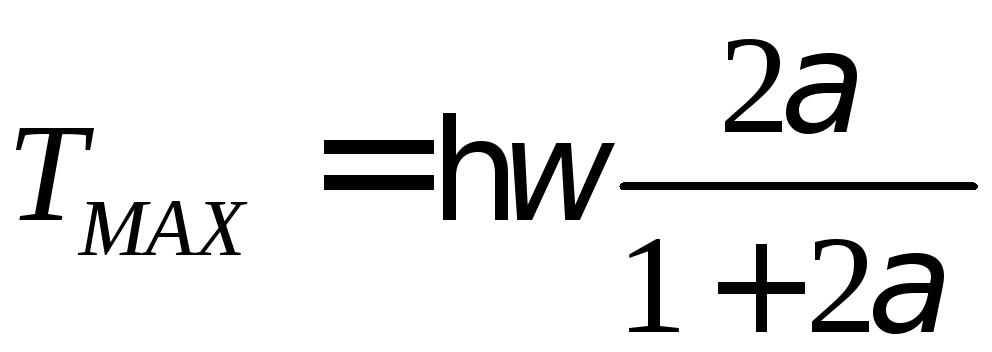 электрон
отдачи приобретает при
= ,
т.е. при рассеянии “назад”.
электрон
отдачи приобретает при
= ,
т.е. при рассеянии “назад”.
В заключение отметим, что наблюдение Комптон-эффекта возможно и на других заряженных частицах, например, на протонах. Однако из-за большой массы протона его отдача заметна лишь при рассеянии фотона очень высокой энергии. Возможно также увеличение энергии (частоты) и импульса (уменьшение длины волны) рассеянного фотона при взаимодействии его с релятивистским (высокоэнергетическим, движущимся со скоростью, близкой к скорости света) электроном. Это явление получило название обратный эффект Комптона.
Заметим, что в реальном эксперименте наряду со смещённой (комптоновской) линией, наблюдается некоторый фон. Этот фон, вместе с космическим фоном и аппаратурным шумом содержит в спектре рассеяния и несмещённую (т.е. обладающую той же энергией что и исходное излучение) линию. При рассмотрении механизма комптоновского рассеяния мы предполагали, что фотон “соударяется” со свободным электроном. Для лёгких атомов и для периферических, слабосвязанных электронов, такое предположение вполне оправдано, но внутренние электроны, особенно в тяжёлых атомах, связаны настолько сильно, что их уже нельзя рассматривать как свободные. Поэтому при “соударении” фотон обменивается энергией и импульсом с атомом в целом. Так как масса последнего велика по сравнению с массой электрона, то по закону сохранения энергии и импульса фотон практически не передаёт атому своей энергии (так отскакивает шарик от стенки с бесконечно большой массой при упругом ударе) и, следовательно, его длина волны при рассеянии на атоме не меняется (рэлеевское рассеяние).
Комптоновское и рэлеевское рассеяние не исчерпывают всех механизмов взаимодействия электромагнитного излучения с веществом. Среди прочих следует упомянуть фотоэлектронное поглощение (фотоэффект), представленное работой в нашем лабораторном практикуме, образование электрон-позитронных пар, резонансные и др. эффекты, способные доминировать в определённых условиях этого взаимодействия.
Имитационная компьютерная модель полностью воспроизводит функции реальной установки. Для её запуска нужно активировать (запустить) программу atomic_d, дважды щёлкнув по её ярлыку левой кнопкой мыши (ЛКМ). При этом на экране монитора должна появиться заставка, показанная на рис. 3. Заставку можно развернуть во весь экран (если она не
Рис. 3. Экранная заставка работы “Эффект Комптона”
развёрнута)
однократным щелчком ЛКМ по кнопке “”
в правом верхнем углу окна (см. указатель
(1) на рис. 3). После этого однократный
щелчок ЛКМ по надписи (2) “Эффект Комптона”
приводит в рабочее окно программы (рис.
4). Далее окно нужно центрировать нажатием
указателя “![]() ”
(показан стрелкой (3) на рис. 4). В результате
центрирования на экране появятся все
управляющие элементы установки (рис.
5).
”
(показан стрелкой (3) на рис. 4). В результате
центрирования на экране появятся все
управляющие элементы установки (рис.
5).
Две области рабочего окна, показанные на рис. 5 представ-

Рис. 4. Рабочее окно программы после щелчка ЛКМ по надписи “Эффект Комптона”
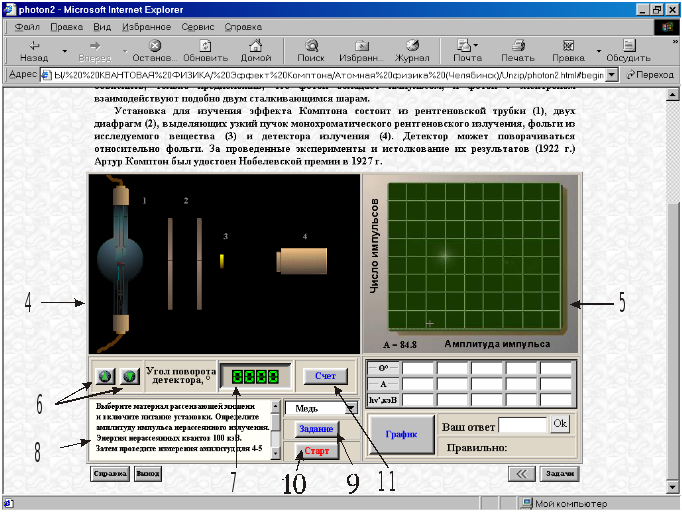
Рис. 5. Рабочее окно перед началом работы
ляют экспериментальную установку (4) и индикаторную панель анализатора углового распределения рассеянных фотонов (5), подключённого к выходу ФЭУ (анализатор в окне установки не показан). Панель (5) будет использоваться в ходе выполнения эксперимента для регистрации зависимостей энергии, частоты и длины волны от угла рассеяния. Кнопки (6) (управление кнопками с помощью ЛКМ) задают угол поворота детектора относительно оси пучка, соответствующий углу рассеяния , может задаваться в положительном (вверх) и отрицательном (вниз) направлениях отсчёта. Значение установленного угла показывается индикатором (7) с указателем “Угол поворота детектора, ”. Функция индикатора в процессе работы может изменяться (см. далее текст описания). Текстовая панель (8) представляет задания, которые меняются с помощью кнопки (9) в ходе выполнения работы. Запуск установки осуществляется нажатием кнопки “Старт” (10), при этом яркость свечения рентгеновской трубки увеличивается, а в правом нижнем углу установки появляется мигающий индикатор (треугольный символ наличия радиоактивности, см. рис. 6). Для начала счёта импульсов от рассеянных квантов при установленном значении угла рассеяния нужно нажать кнопку “Счёт” ((11) на рис. 5), при этом функция индикатора угла меняется. Вместо надписи “Угол поворота детектора, ” появляется “Число импульсов”, и индикатор начинает отображать счёт. При этом на индикаторной панели анализатора возникает амплитудный спектр рассеянного излучения, имеющий форму ступенчатого колоколообразного распределения с максимумом по оси oX в точке, соответствующей энергии рассеянных квантов. Имейте в виду, что счёт импульсов происходит в течение некоторого времени экспозиции, и после его окончания функция индикатора снова меняется (восстанавливается индикация угла), поэтому для регистрации общего числа импульсов за время счёта нужно успеть заметить остановившееся показание индикатора, иначе набор импульсов придётся повторить. При повторном наборе максимальное число зарегистрированных импульсов может быть другим из-за случайной погрешности, обусловленной статистическими свойствами излучения. Вид установки и индикаторной панели анализатора в процессе регистрации излучения при = 0 показан на рис. 6.
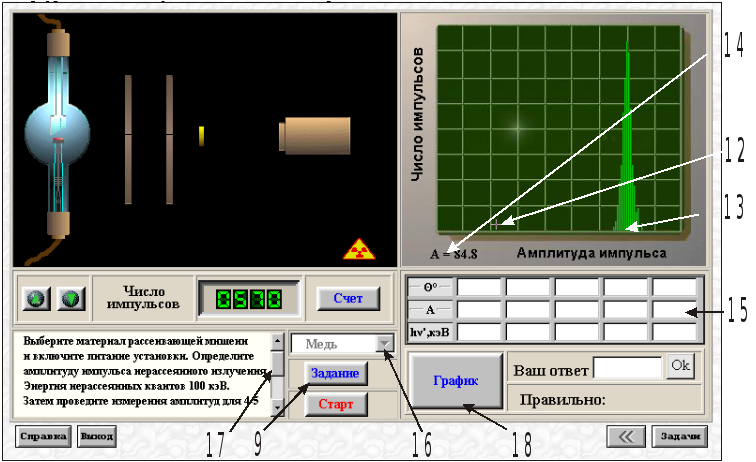
Рис. 6. Установка и индикаторная панель в процессе регистрации рассеянного излучения
По окончании счёта перекрестие (12) на рис. 6 можно с помощью ЛКМ перетащить (нажать ЛКМ, протащить курсор и отпустить) в место расположения максимума спектра рассеяния (13). При этом индикатор (14) “A = ” покажет значение энергии рассеянного излучения в условных единицах амплитуды зарегистрированных импульсов. Если теперь нажать клавиатурную кнопку “Enter”, то значения угла “” и энергии “A” окажутся введёнными в 1-й столбец таблицы (15) индикаторной панели анализатора. Эти данные для разных значений угла придётся несколько раз (5 раз) вводить в процессе выполнения заданий. Значения амплитуды “А” в ходе выполнения заданий нужно будет пересчитать в энергию рассеянных квантов.
Кнопка
(16) позволяет выбрать материал анода
рентгеновской трубки (у каждого студента
в подгруппе свой анод), который
устанавливается по указанию преподавателя
(или персонала лаборатории) из списка,
предлагаемого программой в раскрывающемся
окне после нажатия ЛКМ этой кнопки и
соответствующего выделения. Переход к
выполнению следующего задания происходит
при нажатии кнопки (9) “Задание”, после
которого оно появляется в текстовом
окне. Если весь текст в окне не умещается,
то нужно ЛКМ сдвинуть вниз ползунок
(17) (нажать и протащить). Кнопка (18) “График”
служит для индикации построенного по
вашим данным экспериментального графика
зависимости E()
(обозначение в программе “h()”,
что то же самое, что и
![]() в тексте описания). График появляется
на месте индикаторной панели анализатора
и выглядит, как показано на рис. 7 (окно
(19)). На нём маленькими кружками отмечены
точки теоретической зависимости, а
крестами - ведённые в таблицу точки.
в тексте описания). График появляется
на месте индикаторной панели анализатора
и выглядит, как показано на рис. 7 (окно
(19)). На нём маленькими кружками отмечены
точки теоретической зависимости, а
крестами - ведённые в таблицу точки.
Окно (20) на рис. 7 служит для клавиатурного ввода рассчитанных вами значений параметров опыта - ответов на вопросы заданий работы, а кнопка (21) “Ok” – для подтверждения правильности ввода.
Кнопки
(22) и (23) служит для перехода в режим
контроля и смены контрольных вопросов
(при выполнении заданий работы не
используются), (24) - предназначена для
получения теоретической справки по
теме работы, а (25) - для возврата в начало
программы во входное окно экранной
заставки (рис. 3). При работе со справочными
данными имейте в виду, что текстовое
окно справки можно развернуть во весь
экран так же как это делается при входе
в программу с помощью кнопки (1) на рис.
3 (в справочном окне есть такая же кнопка).
Пролистывание текста возможно с помощью
ползунка, подобного (17) на рис. 6, или в
гипертекстовом режиме установкой мышью
указателя-стрелки на выделенный
фиолетовым цветом текст “(Эффект
Комптона)” до изменения вида указателя
на “ ![]() ”
с последующим
щелчком ЛКМ.
”
с последующим
щелчком ЛКМ.
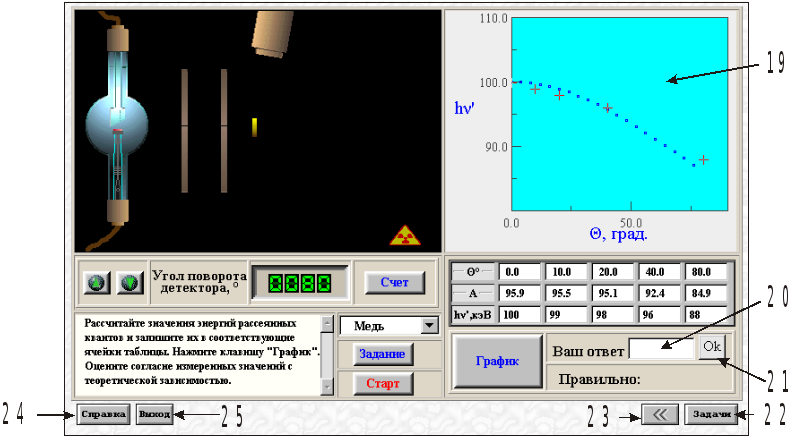
Рис. 7. Установка и график экспериментальных результатов после завершения выполнения задания 2
Перед началом работы поупражняйтесь в установке режимов работы программы с помощью управляющих клавиш и получении указаний-подсказок, доступных в текстовых окнах и приведенных в настоящем описании.
Для окончательного завершения работы программы из любого места её выполнения нужно нажать ЛКМ клавишу “”в самом верхнем правом углу экрана монитора. После этого повторный запуск программы выполняется с самого начала, как описано начиная со с. 7.
