Vorobyev_Volnovaya_optika_Difraktsia

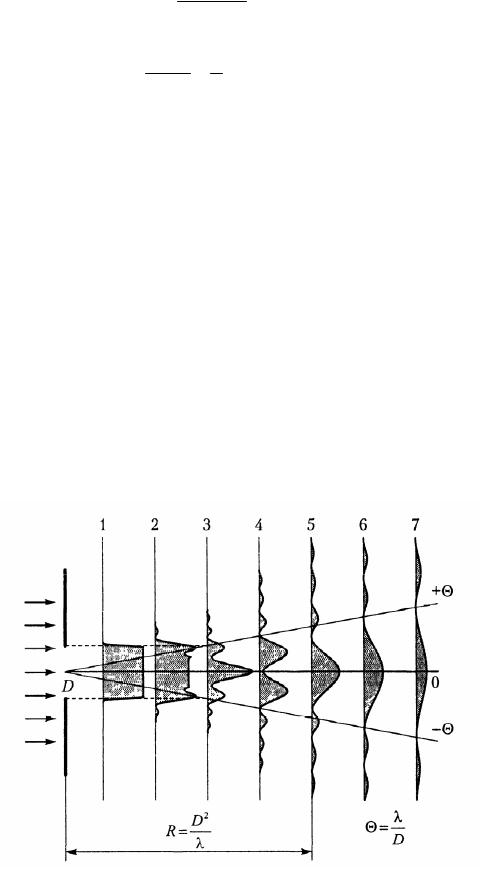
Из рисунка видно, что D sin d , где D - диаметр отверстия. Как

2

правило, дифракционная расходимость невелика ( d <<1), поэтому можно приближенно записать D d , откуда следует, что

Таким образом, дифракционная расходимость светового пучка в дальней зоне определяется отношением длины волны к начальному диаметру пучка D : дифракционная расходимость пучка тем больше, чем меньше его начальный размер. Диаметр пучка в дальней зоне выражается формулой

рана с отверстием. Оценим дифракционную длину bd и угловую расходимость d для пучка гелий - неонового лазера: для D = 2 мм, = 0,6 мкм

получим bd = 1:5 м, d = 3 10-3 рад.

Из всего сказанного в этом разделе следует, что результат дифракции мо-

нохроматического излучения на каком-либо препятствии зависит не от абсолютных его размеров, а от числа m перекрываемых им полуволновых зон.

При m ? 1 (порядка нескольких сотен или тысяч открытых зон) дифракционные эффекты незначительны и распределение интенсивности приближенно описывается законами геометрический оптики (плоскость 1

на рис. 7.4).

21

Рис.7.4. Дифракционные распределения интенсивности света на различных расстояниях от круглого отверстия.

Промежуточное условие (когда открыты единицы или десятки зон) соответствует дифракции Френеля и приводит к сложному распределению интенсивности, когда в центре картины может наблюдаться и минимум, и максимум (плоскости 2, 3 и 4 на рис. 7.4 и рис. 7.1 – ближняя зона).

При m 1 перекрывается малая часть первой зоны и возникает важный для практики случай - дифракция Фраунгофера или дифракции в дальней зоне (плоскости 6 и 7 на рис. 7.4 и рис.7.2 – дальняя зона). Условной границей между двумя видами дифракции считают дистанцию Рэлея

bd R D2 , соответствующую расстоянию, на котором круглое отверстие

диаметра D , освещенное плоской монохроматической волной, открывает для центральной точки наблюдения одну первую зону (m 1).

8. Дифракция Френеля

Дифракция Френеля или дифракция в ближней зоне — это дифракция сферических волн, осуществляемая в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвав-

шего дифракцию. Поверхность волнового фронта на препятствии при дифракции Френеля случае представляет собой участок сферы. Выясним характер дифракционной картины для экрана с отверстием радиусом r0 , при условии r0 <<a и r0 <<b. Из формулы (3.5) и графического анализа с помощью спирали Френеля, следует, что результирующая амплитуда световой волны осциллирует в зависимости от числа зон участвующих в формировании дифракционной картины. Если расстояния a и b удовлетворяют условию

где m - целое число, то отверстие оставит открытым равно m первых зон Френеля. Поэтому вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Амплитуда света в центре экрана, согласно (3.5) будет равна:

где знак «плюс» для случая, когда отверстие открывает нечётное число m число зон Френеля, знак «минус» - для чётного m.

При неизменном b, но при изменении радиуса отверстия r0 , дифракционная картина будет иметь вид чередующихся тёмных и светлых колец,

22

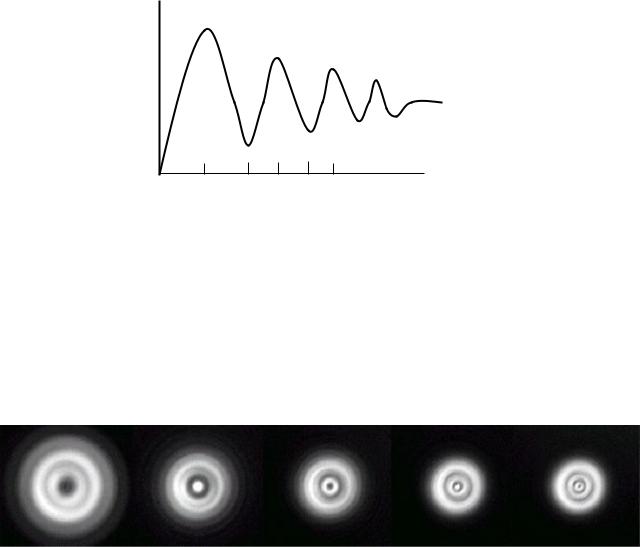
причём в центре будет светлое пятно, если отверстие открывает нечётное число зон, и тёмное пятно, если m – чётное (рис. 8.1)

Аналогичная дифракционная картина наблюдается при неизменном r0 , но при изменении расстояния b. При изменении расстояния b, значение m становится то чётным то нечётными, поэтому максимумы и минимумы интенсивность света в центре дифракционной картины будет чередоваться.

AA1

1

0,5

0

Рис. 8.1. Зависимость относительной амплитуды света в центре дифракционной картины от радиуса отверстия, r1;2;3 - радиусы френелевских зон.

На рис. 8.2 показаны дифракционные картины Френеля, возникающие при дифракции на круглом отверстии по мере приближения к экрану с отверстием. Интенсивность в центре картины осциллирует, при чётных значениях числа зон Френеля m в центре наблюдается тёмное пятно, при нечётных – светлое.

Рис. 8.2. Дифракция Френеля на круглом отверстии при изменении расстояния b. Число открытых полуволновых зон Френеля увеличивается с право на слева от 2 до 6. Размер картины увеличивается, приближаясь к диаметру отверстия

При дифракции Френеля на щели также наблюдаются осцилляции интенсивности света в центра дифракционной картины.

На рис. 8.3 показаны картины дифракции света на длинной щели при изменении её ширины.

23

Рис. 8.3. Дифракция Френеля на одномерной вертикальной щели по мере её расширения (cправа налево). Вертикальный размер дифракционной картины определяется диаметром светового пучка.

Начальная ширина щели соответствует примерно одной открытой полуволновой зоне Френеля, конечная - пяти открытым зонам. Вертикальный размер картины определяется диаметром пучка, падающего на щель.

Дифракция Френеля на непрозрачном диске

Наиболее эффектным доказательством волновой природы света являются дифракционные картины, которые получаются, когда в качестве препятствия используется непрозрачный диск, закрывающий центр светового пятна. Если диск закрывает первые m зон Френеля, то амплитуда колебаний в центре экрана будет равна:

т.е. амплитуда колебаний в центре равна половине амплитуду создаваемой первой открытой зоной. Поэтому при дифракции Френеля на непрозрачном диске в центре дифракционной картины наблюдается интерференционный максимум. Дифракция на дисках различного диаметра приводит к появлению в центре геометрической тени максимума - т.н. пятна Пуассона. Центральный максимум окружён чередующимися концентрическими тёмными и светлыми кольцами (рис. 8.5).

Рис. 8.5. Пятно Пуассона. Дифракция Френеля на непрозрачных дисках разного диаметра. Диаметр и яркость пятна увеличиваются при уменьшении диаметра диска.

24

9. Дифракция Фраунгофера

Если окажется, что расстояние от отверстия до точки наблюдения b таково, что на отверстии укладывается менее одной зоны, то в точке Р будет всегда максимум, а вид дифракционной картины в плоскости экрана, пере-

стает зависеть от величины b. Из формулы (7.2) следует, что такой случай наблюдается, когда m 1, т.е. когда

В этом случае b достаточно велико и можно считать, что лучи, идущие от крайних точек отверстия в точку M параллельны. Такая дифракция в "па-

раллельных лучах" называется дифракцией Фраунгофера.

Таким образом, дифракция Фраунгофера наблюдается, когда источник света и точка наблюдения бесконечно удалены от препятствия вызывающего дифракцию. Фронт волны на препятствии при дифракции Фраунгофера представляет собой плоскость.

На примере дифракции на кольце (рис.9.1) можно проследить плавный переход от геометрической оптики (1-3) через дифракцию Френеля (4-7) к дифракции Фраунгофера (9-11).

Рис. 9.1. Границы дифракционных приближений. Дифракция на кольце. Число открытых зон m уменьшается слева направо, при этом значение m 1 (дистанция Рэлея, условная граница между дифракциями Френеля и Фраунгофера) соответствует снимку 8.

Дифракция Фраунгофера на круглом отверстии

В этом случае дифракционная картина представляет собой чередование светлых и темных колец. В центре дифракционной картины всегда наблюдается светлое пятно (дифракционный максимум). Распределение интенсивности в плоскости экрана наблюдения задается функцией (рис. 9.2):

Iu 2J1 u

u

где J1 u - функция Бесселя, первого рода (см. Приложение 6)

25

Рис. 9.2

Расчет положения минимумов и максимумов в математическом плане сводится к определению корней функции Бесселя J1 u , где

u 2 asin , a - радиус отверстия.

Положение максимумов и минимумов удовлетворяют условию:

sin km m a

где m = 1, 2, 3, 4, ... - порядок максимума или минимума. Значения kмин , kмак и относительные интенсивности максимумов Iотн для m = 1, 2, 3, 4

приведены в таблице.

10. Дифракция Фраунгофера на щели

Рассмотрим дифракцию Фраунгофера плоской монохроматической волны на одной бесконечно длинной щели шириной a (рис. 10.1). Щелью будем называть прямоугольное отверстие, ширина которого во много раз меньше его длины.

Оптическая разность хода между лучами, идущими от краёв щели:

Разобьём открытую часть волновой поверхности на полосчатые полуволновые зоны Френеля, параллельные ребру щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна 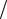2, по-

26

этому на ширине щели уместится m зон Френеля.

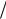2

Поскольку лучи параллельны, то все точки волнового фронта в плоскости щели имеют одинаковую фазу и амплитуду колебаний. Поэтому суммарная интенсивность колебаний от двух любых соседних зон Френеля равна нулю.

Следовательно:

1) если число зон Френеля m укладывающихся в щели чётное,

- условие дифракционного максимума, соответствующего действию од-

ной некомпенсированной зоны Френеля, где - m 0, 1, 2, 3...

Рис.10.1. Дифракция Фраунгофера на одиночной щели

В направлении 0 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью и формирует центральный дифракционный максимум.

27

Из (10.2) и (10.3) следует: направления, в которых амплитуда

минимальна sin min m (10.5) a

Распределение интенсивности на экране, получаемое вследствие дифракции, называется дифракционным спектром. Интенсивности в центральном и последующих максимумах относятся как 1:0,047:0,017:0,0083:..., т.е. основная часть световой энергии сосредоточена в центральном максимуме.

Изменение вида дифракционной картины Фраунгофера при увеличении ширины щели для монохроматического источника света показано на рис. 10.2.

Рис. 10.2. Одномерная дифракция Фраунгофера на вертикальной щели по мере ее расширения слева направо

Нулевой максимум наиболее яркий и вдвое шире побочных максимумов. Размер области дифракционного расплывания обратно пропорционален ширине щели.

Более точный расчёт дифракции на щели даёт формулу распределения интенсивности света на экране Э в зависимости от угла дифракции виде:

где I0 - интенсивность света в середине дифракционной картины (в направлении 0); I - интенсивность света в точке, положение которой определяется данным значением угла . Вид кривой зависимости интенсивности показан на рис. 10.3.

28

интенсивность света равна нулю. Из (10.7) следует уже рассмотренное выше условие главного минимума.

где m 0, 1, 2, 3,....

Условие же максимумов интенсивности отличается от (10.3) и имеет

Однако расчеты показывают, что формула (10.3) по сравнению с (10.3а) дает лишь несущественно завышенные значения угла дифракции n : примерно 5% для n = 1, на 2% для n = 2 и т.д. Такая ошибка пренебрежимо мала, и формулу (10.3) можно считать справедливой. Подставив ее в выражение (10.6), для n = 1, 2, 3 и т.д., получим

Imax 2 nI0 0,5 2 ,

откуда следует, что максимумы Imax высших порядков по сравнению с центральным I0 очень слабые, а именно:

Imax1 0,045I0, Imax2 0,016I0, Imax3 0,008I0 и т.д.

Из (10.6) вытекает, что I I . Это означает, что дифракционная кар-

тина симметрична относительно центра линзы.

При малых углах дифракции координаты минимумов или максимумов на экране из геометрических соображений можно найти по приближённой

29

формуле. Из рис.10.1 следует, что:

x F tg F sin

где F - фокусное расстояние линзы. Отсюда sin x и из условий (10.4)

где n = 0, 1, 2, 3,..

Ширина центрального максимума (рис. 10.1), ограниченная минимумами первого порядка (m = 1), определяется зависимостью

Она увеличивается при уменьшении ширины щели a, что не может быть объяснено законами геометрической оптики.

При a ? дифракция становится слабо выраженной, а на экране наблюдается геометрическое изображение щели. Однако в любом случае дифракцию можно наблюдать только при a . Это следует из формулы (10.5): так как максимальное значение sin m 1, то это возможно при

amin m .

На экране, достаточно удаленном (на расстояние L) от щели дифракцию Фраунгофера можно наблюдать и без собирающей линзы Л, для этого

необходимо, чтобы выполнялось условие L ? a2 . В этом случае формулу

Пучок света, сходящийся в точке x F tg F sin экрана, практически остается параллельным. Из формулы (10.4) и (10.5) в этом случае следует, что координаты минимумов и максимумов при дифракции на щели равны соответственно:

a

где m = 1, 2, 3,..; L - расстояние от плоскости щели до экрана.

30