
Vorobyev_Volnovaya_optika_Difraktsia
.pdf
13. По формулам (14а) для двойной щели рассчитайте ширину щелей a и расстояние между ними d , приняв во внимание что a a cos и d d cos (d a b d ? a).
xm |
m |
|
|
|
L, |
m 1,2,3,... |
|
|
|
|
|||||
|
a |
|
|
||||
xk |
k |
|
L, |
k 0,1,2,3,... |
(14а) |
||
|
|||||||
|
|
d |
|
|
|||
14. Оцените погрешность измерений по формуле Стьюдента и запишите результат в формате:
a  a
a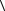 a d
a d 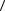 d
d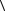 d
d
Задание 2.
Дифракция на четырёх щелях и на дифракционной решётке
1. Повернув турель 2, установите под лазерный луч пластинку с четырьмя щелями. Убедитесь, что плоскость пластинки перпендикулярна световому пучку (угол 0 ).
3.Сфотографируйте и сохраните изображения дифракционных картин для углов 0 , 30 и 60 .
4.Повернув турель 2, установите под лазерный луч пластинку с одномерной дифракционной решёткой. Сфотографируйте и сохраните изображения дифракционных картин для углов 0 , 30 и 60 .
5.Выключите лазерный источник света.
6.По сохранённым снимкам с помощь программы «skopephoto» определите расстояние от центра нулевого максимума (центра дифракционной картины) до центра первого интерференционного максимума xk1 . Данные
занесите в таблицу 2.
|
|
|
Таблица 2 |
|
|
|
|
|
|
четыре щели |
дифракционная |
|||
|
|
|
решётка |
|
угол |
xm , мм. |
xk , мм. |
угол |
xk , мм. |
0о |
|
|
|
|
30о |
|
|
|
|
60о |
|
|
|
|
7. По формулам (14а) рассчитайте ширину щелей a и постоянную дифракционной решётки d (расстояние между центрами щелей d a b d ? a), приняв во внимание, что a a cos и d d cos
71
где a и d - кажущая ширина щелей и кажущаяся постоянная дифракционной решётки.
72

Задание 3.
Дифракция на двумерной дифракционной решётке
1. Повернув турель 2, установите под лазерный луч двумерную дифракционную решетку. Убедитесь, что плоскость пластинки перпендикулярна световому пучку (угол 0 ).
3.Сфотографируйте и сохраните изображения дифракционных картин для углов 0 , 30 и 60 .
4.Выключите лазерный источник света.
5.По сохранённым фотографиям определите расстояние от центра нулевого максимума (центра дифракционной картины) до центра первого интерференционного максимума xk1 по оси X и до первого интерферен-
ционного максимума yk1 по оси Y. Данные занесите в таблицу 3. Таблица 3
двумерная дифракционная решётка
угол |
xk1 |
yk2 |
0о
30о
60о
6. По формулам (22а) рассчитайте dx и dу постоянные двумерной ди-
фракционной |
решётки по осям |
X и Y, приняв |
во внимание, что и |
||||
d d cos где d - кажущаяся постоянная дифракционной решётки. |
|||||||
xk |
k |
|
L, |
k 0,1,2,3,... |
|
||
|
|
|
|||||
|
|
d |
|
|
|||
y |
k |
|
L, |
k 0,1,2,3,... |
(22а) |
||
|
|||||||
k |
d |
|
|
||||
|
|
|
|||||
5. Оцените погрешность измерений по формуле Стьюдента и запишите результат в формате:
dx  dx
dx  d dy
d dy  dy
dy  d
d
73

7. ЛАБОРАТОРНАЯ РАБОТА № 3.41 ДИФРАКЦИЯ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
Цель работы: Определение ширины щели и постоянной дифракционных решеток по дифракционным картинам на экране наблюдения.
Оборудование: Модульный учебный комплекс ЛКО-1.
Методика эксперимента
Лабораторная работа выполняется на модульном учебном комплексе ЛКО – 1 (Приложение 5). Для определения параметров объектов № 23, 23, 27 и т. д. необходимо получить на фронтальном экране их дифракционные изображения и используя шкалу экрана определить расстояние от центра дифракционной картины до первого дифракционного минимума и первого интерференционного (главного) максимума. Для этого необходимо предварительно выполнит калибровку микропроектора.
Калибровка заключается в определении поперечного увеличения линзы микропроектора. Для калибровки устанавливают микропроектор (модуль 3) на оптической скамье, а перед ним - модуль 5 или другой элемент так, чтобы лазерный пучок расширился и осветил в плоскости микропроектора площадку диаметром 5-10 мм, при этом на экране будет освещена площадка диаметром несколько сантиметров. Размещая в кассете микропроектора различные объекты, получают на экран их увеличенное изображение.
Установите в кассете микропроектора объект № 2 с калибровочной сеткой, цена деления h которой 1,00 мм. По шкале экрана определите координаты изображений нескольких штрихов сетки и найдите расстояние Н между соседними изображениями.
ВНИМАНИЕ! Координата центра исследуемого изображения по шкале экрана должна быть на 30 10 мм. больше координаты риски микропроектора по шкале оптической скамьи (см. рис. 8)! При нарушении этого условия увеличиваются погрешности измерений.
Увеличение микропроектора
H h |
(1) |
Если измеряемые размеры составляют несколько миллиметров, то исследуемое распределение интенсивностей проецируют на круглый экран со шкалами модуля 5. Если же характерные размеры составляю доли миллиметра, то используют микропроектор.
Исследуемое распределение (например, дифракционную картину) или измеряемый объект размещают в объектной плоскости линзы модуля 3. Увеличенное изображение - наблюдают на экране фотоприемника и измеряют размер Н изображения. Размер объекта определяется по формуле:
h H |
(2) |
где - коэффициент увеличения микропроектора.
74
Порядок выполнения работы
1.Перед началом работы изучите теорию явления дифракции на щели
ина дифракционной решетке.
2.Изучите устройство и правила эксплуатации комплекса ЛКО-1 и используемых в работе модулей в Приложении 5.
2.Ознакомьтесь с порядком включения и выключения лазерного источника света и инструкцией по технике безопасности. Обратите особое внимание на недопустимость попадания в глаза прямого лазерного излучения.
3*. Включите лазерный источник света.
Внимание. Пункты, помеченные звёздочкой, выполняет преподаватель или лаборант.
Задание 1.
Дифракция на одиночной и двойной щелях
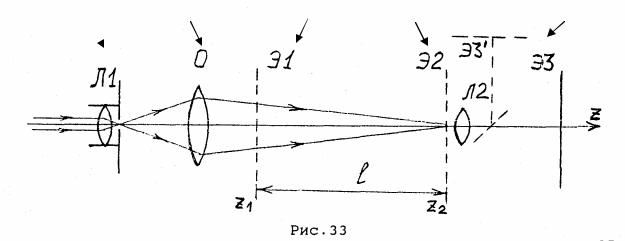
1. Соберите на оптической скамье комплекса устройство для наблюдения дифракции согласно схеме на рис. 33.
модуль 5 |
|
модуль 6 |
|
модуль 8 |
|
модуль 3 |
|
модуль 4 |
конденсор |
|
объектив |
|
кассета |
|
микропроек. |
|
фоторегистр. |
|
|
|
|
|
|
|
|
|
2. Установите в кассету координатного стола (модуль 13) одиночную щель (объект № 23) в положение перпендикулярное направлению лазерного пучка (угол 0 )..
3*. Включите лазерный источник света.
Внимание. Пункты, помеченные звёздочкой, выполняет преподаватель или лаборант.
4. Зарисуйте дифракционную картину. Определите координаты положение минимума xm1 и максимума xn1 первого порядка, т.е. измерьте расстояние от центра дифракционной картины до центра первого минимума и до центра первого максимума.
75

3.Поверните щель на угол 30 и далее на 60 по отношению к первоначальному положению. Пронаблюдайте изменения дифракционной картины и зарисуйте её.
4.Определите координаты положение минимума и максимума первого порядка при углах 30о и 60о. Все данные занесите в таблицу.
5.Установите на место одиночной щели пластинку с двумя щелями (объект 27). Убедитесь, что плоскость пластинки перпендикулярна световому пучку (угол 0 ). Зарисуйте дифракционную картину.
6.Определите координаты положение первого дифракционного мини-
мума xm1 и главного интерференционного максимума первого порядка xk1
при углах 0 , 30о и 60о для двойной щели. Данные занесите в таблицу. 7. Выключите лазерный источник света.
Таблица 1.
одиночная щель |
|
|
|
|
двойная щель |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угол |
x |
m |
|
Xm |
, |
x |
n |
|
Xn |
|
угол |
x |
m |
|
Хm |
, |
|
x |
k |
|
Xk |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
мм |
|
|
|
|
|
|
|
|
мм |
|
|
|
мм |
|
|||||
0о |
|
|
|
|
|
|
|
|
|
|
0о |
|
|
|
|
|
|
|
|
|
|
|
30о |
|
|
|
|
|
|
|
|
|
|
30о |
|
|
|
|
|
|
|
|
|
|
|
60о |
|
|
|
|
|
|
|
|
|
|
60о |
|
|
|
|
|
|
|
|
|
|
|
8. По формулам (8) с учётом увеличения микропроектора рассчитайте ширину a одиночной щели при угле 0 и при углах 30 и 60 учитывая, что при наклонном падении эффективный (кажущийся) размер
ширины щели a a cos . |
|
|
|
|
|
|
|
|
|||
xm |
m |
|
|
L, |
|
|
|
m 1,2,3,... |
|
||
|
|
|
|
|
|||||||
|
a |
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
xn |
n |
|
|
|
|
|
L, |
n 0,1,2,3,... |
(8) |
||
2 |
a |
||||||||||
|
|
|
|
|
|
|
|||||
где xm и xn - координаты m -го минимума и n -го максимума, - длина волны лазерного излучения, a - ширина щели, L - расстояние от щели до экрана.
9. Найдите среднее значение, рассчитайте погрешность и запишите результат в формате:
a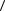 a
a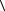 a
a
10.По формулам (14а) для двойной щели с учётом увеличения микропроектора рассчитайте ширину щелей a и расстояние между ними d ,
приняв во внимание что a a cos и d d cos (d a b d ? a).
76
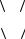
xm |
m |
|
|
|
L, |
m 1,2,3,... |
|
|
|
|
|||||
|
a |
|
|
||||
xk |
k |
|
L, |
k 0,1,2,3,... |
(14а) |
||
|
|||||||
|
|
d |
|
|
|||
11. Оцените погрешность измерений по формуле Стьюдента и запишите результат в формате:
a 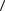 a
a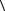 a d
a d 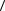 d
d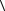 d
d
Задание 2.
Дифракция на четырёх щелях и на дифракционной решётке
1. Установите под лазерный луч пластинку с четырьмя щелями. Убедитесь, что плоскость пластинки перпендикулярна световому пучку (угол
0 ).
3. Зарисуйте изображения дифракционных картин для углов 0 ,
30 и 60 .
4.Установите под лазерный луч пластинку с одномерной дифракционной решёткой. Зарисуйте изображения дифракционных картин для углов
0 , 30 и 60 .
5.Выключите лазерный источник света.
6.По рисункам определите расстояние от центра нулевого максимума (центра дифракционной картины) до центра первого дифракционного ми-
нимума xm и до центра первого интерференционного максимума xk . Дан-
ные занесите в таблицу 2.
|
|
|
|
|
|
|
|
|
Таблица 2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
четыре щели |
|
|
|
дифракционная решётка |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xm |
Xm |
|
|
xk |
Xk |
|
|
xk |
Xk |
|
угол |
|
, |
|
|
, |
угол |
|
, мм. |
|||
|
|
|
|||||||||
|
мм. |
|
|
мм. |
|
|
|
|
|
||
0о |
|
|
|
|
|
|
|
0о |
|
|
|
30о |
|
|
|
|
|
|
|
30о |
|
|
|
60о |
|
|
|
|
|
|
|
60о |
|
|
|
7. По формулам (14а) учётом увеличения микропроектора рассчитайте ширину щелей a и постоянную дифракционной решётки d (расстояние между центрами щелей d a b d ? a), приняв во внимание, что a a cos и d d cos где a и d - кажущая ширина щелей и кажущаяся постоянная дифракционной решётки.
8. Оцените погрешность измерений по формуле Стьюдента.
77

9. Запишите результат в формате: a 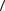 a
a a
a
d  d
d d
d
Задание 3.
Дифракция на двумерной дифракционной решётке
1. Повернув турель 2, установите под лазерный луч двумерную дифракционную решетку. Убедитесь, что плоскость пластинки перпендикулярна световому пучку (угол 0 ).
3. Зарисуйте изображения дифракционных картин для углов 0 ,
30 и 60 .
4.Выключите лазерный источник света.
5.Определите расстояние от центра нулевого максимума (центра ди-
фракционной картины) до центра первого интерференционного максимума xk1 по оси X и до первого интерференционного максимума yk1 по оси Y.
Данные занесите в таблицу 3.
|
|
|
|
|
|
|
|
|
Таблица 3 |
|
|
|
|
|
|
|
|
|
|||
двумерная дифракционная решётка |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
угол |
x |
|
|
Xk |
, мм. |
y |
|
Yk |
, мм. |
|
|
|
k |
|
|
k |
|
|
|
||
0о |
|
|
|
|
|
|
|
|
|
|
30о |
|
|
|
|
|
|
|
|
|
|
60о |
|
|
|
|
|
|
|
|
|
|
6. По формулам (22а) с учётом увеличения микропроектора рассчитайте dx и dу постоянные двумерной дифракционной решётки по осям X
и Y, приняв во внимание, что и d d cos |
где d |
- кажущаяся постоян- |
||||||
ная дифракционной решётки. |
|
|
|
|||||
xk |
k |
|
L, |
k 0,1,2,3,... |
|
|
||
|
|
|
|
|||||
|
|
d |
|
|
|
|||
y |
k |
|
L, |
k 0,1,2,3,... |
|
(22а) |
||
|
|
|||||||
k |
d |
|
|
|
||||
|
|
|
|
|||||
5. Оцените погрешность измерений по формуле Стьюдента и запишите
результат в формате: |
|
|
|
dx dx |
d |
dy dy |
d |
78
8. ЛАБОРАТОРНАЯ РАБОТА № 3.42 ДИФРАКЦИЯ ФРЕНЕЛЯ НА КРУГЛОМ ОТВЕРСТИИ
Цель работы – Изучение дифракции Френеля и Фраунгофера на круглом отверстии и определение длины волны излучения.
Оборудование – модульный лабораторный учебный комплекс ЛКО-1.
Методика эксперимента
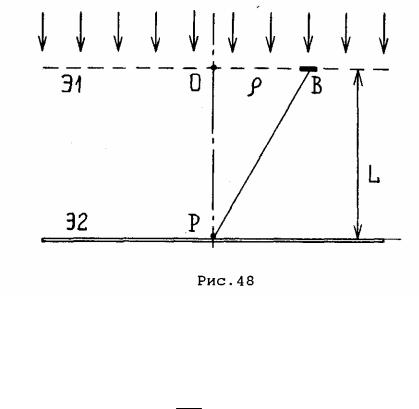
В соответствии с принципом Гюйгенса-Френеля волновое поле, т. е. распределение интенсивности света, на экране Э2 (рис.48) рассматривается как результат суперпозиции волн, испущенных «вторичными» источниками, расположенными на волновой поверхности, например, в плоскости экрана Э1 и когерентными с полем падающей волны.
Пусть плоская волна падает нормально на экран Э1 параллельно его оси симметрии ОР. Расчёт показывает, что колебание, приходящее в точку Р из точки В, запаздывает по фазе относительно колебания, приходящего от точки О, на величину
2 |
(66) |
. |
L
Участок волновой поверхности в плоскости экрана Э1, в пределах которого фаза приходящих в точку Р колебаний изменяется на , называется зоной Френеля. Первая зона Френеля - кружок с центром в точке О, для которого 0 . Для второй (кольцевой) зоны 2 и т.д. Условиеm определяет количество m (целое или дробное) зон, укладываю-
79

щихся в круге радиуса ‚ или радиус m участка, на котором укладываются m первых зон Френеля (он же – радиус внешней границы m-й зоны):
m |
2 |
|
(67) |
||
L |
|||||
|
|
||||
m |
|
|
(68) |
||
|
m L |
||||
Сопоставляя (67) и (63), отметим, что если - характерный размер отверстия в экране Э1, то число m является параметром дифракции, определяющим вид дифракции и дифракционной картины.
Если на экран Э1 падает расходящаяся волна от точечного источника S (рис. 49а) или волна, сходящаяся в точке S (рис. 49б), то вычисления фазовых сдвигов и количества открытых зон Френеля приводят к тем же формулам (66) - (67), что для плоской волны, в которых, однако, L выражается через расстояние l1 от фокуса волны до экрана Э1 и расстояние l от экрана Э1 до экрана Э2.
Для расходящейся волны |
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
1 |
|
1 |
|
(69) |
||||
|
|
|
|
|
|
|
||||||
|
L |
l1 |
|
l |
|
|
||||||
Для сходящейся волны |
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
1 |
|
1 |
|
(70) |
||||
|
|
|
|
|||||||||
|
L |
l |
l1 |
|
|
|||||||
Плоской волне, очевидно, соответствует l1 , L l .
Если в сходящейся волне расстояние l l1 , (т.е. картина наблюдается в фокальной плоскости) то L1 и m 0, наблюдается дифракционная
80
