

Глава 3. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
3.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Функциональной последовательностью (ФП) называют после-
довательность { fn (x)}, элементами которой являются функции
f1 (x), f2 (x),..., fn (x),...,
определенные на некотором множестве A, называемой областью определения этой последовательности.
ФП { fn (x)} называется равномерно ограниченной на множе-
стве A, если выполняется одно из двух эквивалентных условий:
1) |
$C Ρ "n "x ΠA |
|
fn (x) |
|
< C ; |
||||
|
|
||||||||
2) |
$C Ρ "n sup |
|
fn (x) |
|
< C . |
||||
|
|
||||||||
|
x A |
|
|
|
|
||||
ФП { fn (x)} называется возрастающей на множестве A (или возрастающей в каждой точке множества A), если
x A n fn+1 (x) < fn (x).
Аналогично определяются убывающая, невозрастающая и неубывающая ФП.
ФП { fn (x)} называется сходящейся в точке x0 A, если число- вая последовательность { fn (x0 )} сходится.
ФП называется сходящейся (или поточечно сходящейся) на множестве A, если она сходится в каждой точке этого множества.
Если ФП { fn (x)} на множестве A сходится поточечно к предельной функции f (x) , то символически это записывают следующим образом:
x A f (x) = lim fn (x) |
|
|
или |
|
|
fn (x)→ f (x). |
|||||||||||||
n→∞ |
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
A |
|||||
П р и м е р 3.1. Предельная функция |
|
последовательности |
|||||||||||||||||
fn (x) = n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x4n + x−2n + 4n |
|||||||||||||||||||
|
|
ì |
−2 |
, 0 < |
|
|
x |
|
< 0,5; |
||||||||||
|
|
|
|
|
|||||||||||||||
имеет вид f (x) = max{x4 , x−2 ,4}= |
ïx |
|
|
|
|
|
|||||||||||||
í3, 0,5 £ |
|
x |
|
£ |
|
|
|||||||||||||
|
|
2; |
|||||||||||||||||
|
|
ï |
4 |
|
|
x |
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
2. |
|
|
|||||||||||||
|
|
îx |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43
3.2. РАВНОМЕРНАЯ СХОДИМОСТЬ
Последовательность { fn (x)} сходится к f (x) равномерно на
множестве A, если |
|
"e > 0 $n0 "n ³ n0 "x Î A fn (x) - f (x) < e. |
(3.1) |
Обозначение: fn (x)®® f (x).
A
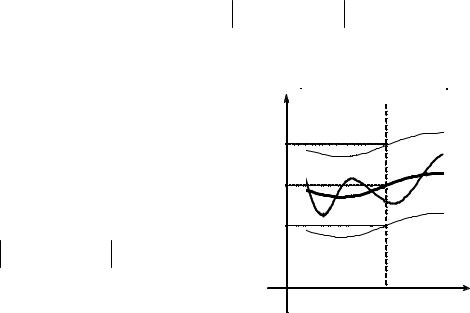
Сущность равномерной сходимо- сти ФП состоит в том, что ε > 0 можно выбрать такой номер n0 (e),
зависящий только от заданного ε и
не зависящий от выбора точки x A, что при n ³ n0 (e) неравенство
fn (x) - f (x) < e
будет выполняться всюду на множе- стве A, т.е. «графики» функций fn (x)
расположены в «ε -полоске», окружа- ющей график функции f (x) (рис. 1).
y |
|
f +ε |
f (x0)+ε |
|
|
|
fn |
|
|
|
|
f (x0) |
|
f |
f (x0)−ε |
|
f −ε |
|
|
|
0 |
x0 |
x |
Рис. 1
Таким образом, в случае равномерной сходимости ε > 0 при всех достаточно больших n (а именно при n ³ n0 (e)) значения
функции fn (x) приближают функцию f (x) с погрешностью, меньшей ε , сразу на всем множестве A.
Лемма 3.1. Если fn (x)®→ f (x), то fn (x)→ f (x). |
|
A |
A |
|
|
Если условие равномерной сходимости не выполняется, т.е.
$e0 |
> 0 "k $n ³ k $x Î A |
|
fn (x) - f (x) |
|
³ e0 , |
(3.2) |
|
|
|
||||||
то ФП { fn (x)} |
не сходится равномерно к f (x) на множестве A. |
||||||
В этом случае пишут fn (x) ®→ f (x). |
|
||||||
|
A |
®→ f (x), то говорят, что ФП { fn (x)} |
|||||
Если fn (x)→ f (x), но fn (x) |
|||||||
|
A |
A |
|
||||
|
|
|
|||||
сходится к f (x) на множестве A неравномерно.
44
Равномерная сходимость ФП на множестве A является глобаль- ным свойством, характеризующим поведение последовательности на множестве «в целом», т.е. множество рассматривается как еди- ный объект. Поэтому недопустима формулировка локального типа: «последовательность равномерно (неравномерно) сходится в точках множества A». В то же время определение равномерной сходимости имеет смысл и для множества A, состоящего из одной точки: A = {x0 } , и эквивалентно в этом случае сходимости последователь-
ности в точке x0 . Если мы хотим говорить о равномерной сходимо- сти в таком случае, то формулировка должна быть следующей:
«ФП сходится равномерно на множестве A = {x0 } » (т.е. не в точке x0 , а на множестве, состоящем из одной точки x0 ).
Для практического исследования равномерной сходимости
удобно использовать следующую теорему. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Теорема 3.1. fn (x)®→ f (x) |
|
limsup |
|
fn (x) - f (x) |
|
= 0. |
|
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
A |
|
|
|
|
|
|
n→∞ x A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
fn (x)®® f (x) "e>0 $n0 "n ³n0 "xÎA |
|
fn (x)- f (x) |
|
£e |
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
A |
|
|
|
|
|
|
|
|
|
|
fn (x)- f (x) |
|
|
|
|
|
|
|
|
|
||||||||||||||||
"e>0 $n0 "n ³n0 sup |
|
|
|
£e |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
æ |
|
|
|
|
|
|
x A |
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
fn (x)- f (x) |
|
= 0. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
limçsup |
|
÷ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
n→∞ è |
x A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
ФП fn (x) = xn |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
П р и м е р 3.2. Покажем, |
что на множестве [0,1) |
|||||||||||||||||||||||||||||||||||
сходится к функции f (x)=0 неравномерно, |
но на любом полуин- |
|||||||||||||||||||||||||||||||||||
тервале [0,α), α<1, сходимость равномерная. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Очевидно, что "x Î 0,1 |
|
lim xn = 0, поэтому для определения |
||||||||||||||||||||||||||||||||||
[ |
|
) |
|
|
n→∞ |
fn (x) - f (x) |
|
|
|
|
|
|
||||||||||||||||||||||||
характера сходимости вычислим lim sup |
|
|
. Так как |
|||||||||||||||||||||||||||||||||
|
|
fn (x)- f (x) |
|
|
|
|
n→∞ x [0,α) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
sup |
|
|
= sup |
|
xn |
|
= sup xn = an , |
(3.3) |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
x [0,α) |
|
|
|
|
|
|
|
|
|
|
x [0,α) |
|
|
|
|
|
|
x [0,α) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim sup |
|
fn (x) - f (x) |
|
= liman |
|
|
ì0, aÎ 0,1 ; |
|
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
= í |
[ |
) |
|
|
|
|
|
|||||||||||||||||||||||||||
n→∞ x [0,α) |
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
1, a =1. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Следовательно, на полуинтервале [0,α), |
î |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
α < 1, сходимость равно- |
|||||||||||||||||||||||||||||||||||
мерная, а на полуинтервале |
[ |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0,1 – неравномерная. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
45

Теорема 3.2 (критерий Коши равномерной сходимости).
Для того чтобы ФП { fn (x)} равномерно на множестве A сходилась к некоторой предельной функции, необходимо и достаточно, чтобы
"e>0 $n0 =n0 (e) "n,m³n0 "xÎA |
|
fn (x)- fm (x) |
|
<e (3.4) |
||||
|
|
|||||||
или |
$n0 =n0 (e) "n ³n0 "pÎ¥ "xÎA |
|
|
fn+ p (x)- fn (x) |
|
<e. (3.5) |
||
"e>0 |
|
|
|
|||||
Необходимость. Пусть ε > 0 задано. По определению равно-
мерной сходимости $n0 (e) "n ³ n0 |
"xÎ A |
|
fn (x)- f (x) |
|
|
< |
ε |
. |
|||||||||||||
|
|
||||||||||||||||||||
|
|
|
2 |
||||||||||||||||||
Тогда "m ³ n0 (e) "x Î A |
|
|
|
|
|
|
|
ε |
|
ε |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
fn (x)- fm (x) |
|
£ |
|
fn (x) - f (x) |
|
+ |
|
fm (x)- f (x) |
|
< |
+ |
= e. |
||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
2 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Достаточность. Выполнение условий теоремы означает сходи- мость ФП { fn (x)} при любом фиксированном x A и существова-
ние предельной функции f (x). Перейдя к пределу в неравенстве fn (x)- fm (x) <e при m→∞ , получим fn (x)- f (x) £e .
З а м е ч а н и е . Утверждения (3.4) и (3.5) можно записать в виде:
"e>0 $n0 =n0 (e) "n,m³n0 sup fn (x)- fm (x) <e,
x A
"e>0 $n0 =n0 (e) "n ³n0 "pÎ¥ sup fn+ p (x)- fn (x) <e .
x A
Теорема 3.3. Если все члены ФП непрерывны на замкнутом множестве A, а сама ФП сходится равномерно на множестве int A его внутренних точек, то ФП сходится равномерно и на множестве A.
Утверждение теоремы следует из критерия Коши, если учесть, что
для всякой непрерывной на замкнутом множестве функции sup f (x)= sup f (x).
x A |
x int A |
Следствие. Если ФП непрерывных на замкнутом множестве A
функций сходится на множестве его внутренних точек и расходится хотя бы в одной из его граничных точек, то сходимость на A нерав- номерная.
П р и м е р |
3.3. Последовательность |
|
fn (x) = |
n |
|
|
сходится к |
|||
|
n2 x |
+1 |
||||||||
функции |
f (x)=0 |
неравномерно на |
( |
) |
|
|||||
|
|
0,1 |
, так как числовая последо- |
|||||||
вательность |
fn (0) = n расходится. |
|
|
|
|
|
|
|
||
46
3.3.СВОЙСТВА РАВНОМЕРНО СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
1.Основные свойства
1. Если |
|
fn (x)→→ f (x) и gn (x)→→ g ( x) , то: |
|||||||
|
|
|
|
A |
A |
||||
|
α,β¡ αfn (x) +βgn (x) →→ αf (x) + βg (x); |
||||||||
|
|
|
|
|
|
|
|
|
A |
2. Если |
|
fn (x) |
|
→→ |
|
f (x) |
|
, то |
fn (x)→→ f (x). |
|
|
|
|
||||||
|
|
|
|
A |
A |
||||
3. Если |
|
fn (x)→→ f (x), то B A fn (x)→→ f (x). |
|||||||
|
|
|
|
A |
B |
||||
Следствие. Если ФП { fn (x)}, определена на множестве Q и для некоторого A Q fn (x) →→ f (x), то B A B Q fn (x) →→ f (x).
A |
|
B |
4. Если fn (x)→→ f (x) и |
fn (x) →→ f (x), то |
fn (x) →→ f (x). |
A |
B |
AUB |
Для бесконечного объединения это утверждение неверно.
5. Числовую последовательность можно рассматривать как ФП, каждый элемент которой есть константа на данном множестве. Сходимость такой ФП на любом множестве равномерна.
6. Если fn (x)→→ f (x) и функция g(x) ограничена на множестве A,
A
то fn (x)g (x)→→ f (x)g (x).
A
7. Если fn (x)→→ f (x) и все члены ФП являются многочленами
A
степени не выше k , то и предельная функция этой ФП также много- член степени не выше k .
8. Если fn (x)→→ f (x) и все члены ФП являются ограниченными
A
на множестве A функциями, то и предельная функция будет огра- ничена на множестве A .
9. Если fn (x)→→ f (x) и функция f (x) |
ограничена на множестве |
A |
|
A, то при некотором n0 ¥ ФП gn (x) = |
fn0 +n (x) равномерно огра- |
ничена на A. |
|
47
2. Предельный переход
Теорема 3.4. Пусть a – произвольная предельная точка множе- ства A. Если fn (x)→→ f (x) и все элементы ФП { fn (x)} имеют
A
в точке a конечное предельное значение, то и предельная функция f (x) имеет в точке a предельное значение, причем
lim f (x) = lim(lim fn (x)) = lim(lim fn (x)), |
||
x→a |
x→a n→∞ |
n→∞ x→a |
т.е. символ lim |
предела последовательности и символ lim предель- |
n→∞ |
x→a |
ного значения функции можно переставлять местами (или, как говорят, к пределу при x → a можно переходить поэлементно).
3. Непрерывность предельной функции
Теорема 3.5. Если fn (x) →→ f (x) и все члены ФП являются
[a,b]
непрерывными на [a,b] функциями, то и предельная функция f (x) будет непрерывна на [a,b] .
З а м е ч а н и е 1 . В теореме 3.5 вместо сегмента [a,b] можно взять интервал, полуинтегрвал, луч или всю вещественную прямую.
Пусть A произвольный промежуток и fn (x)→→ f (x) . Пока-
A
жем, что из непрерывности элементов ФП следует непрерывность предельной функции. Пусть x0 – произвольная точка множества A. Тогда существует отрезок [a,b] такой, что x0 [a,b] и [a,b] A .
Для этого отрезка все условия теоремы 3.5 выполнены, следователь- но, f (x) непрерывна на [a,b] , и в частности в точке x0 . В силу
произольности выбора точки x0 , получаем непрерывность f (x) на всем множестве A.
48

З а м е ч а н и е 2 . Теорема 3.5 может быть использована для доказательства неравномерности сходимости. Если рассматривается сходящаяся ФП, члены которой непрерывны на множестве A, но предельная функция является разрывной, то ФП сходится нерав- номерно на множестве A.
П р и м е р 3.4. На сегменте [0,1] последовательность непрерывных
( ) ì0, x ¹ 1,
функций fn (x) = xn сходится к разрывной функции f x = í
î1, x =1,
поэтому сходимость неравномерная (Отметим, что в примере 3.2 неравномерность сходимости была доказана по определению).
З а м е ч а н и е 3 . Требование равномерной сходимости в тексте теоремы не может быть опущено, доказательством этого может служить предыдущий пример. Однако равномерная сходимость
фигурирует в теореме лишь как достаточное условие непрерывности предельной функции.
П р и м е р 3.5. Покажем, что |
|
|
nx |
|
|
|
®® 0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
1+ n |
2 |
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
|
|
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
nx |
|
|
é |
æ |
|
nx |
|
ö |
¢ |
|
n 1-3n |
2 |
x |
4 |
) |
ù |
|
n × 4 |
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
|
|
|
|
|
||||||||||
lim sup |
|
|
|
|
= êç |
|
|
|
|
|
÷ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
=lim |
|
|
|
|
|
|
® 0 . |
||||
|
2 |
x |
4 |
1+ n |
2 |
x |
4 |
(1+n |
2 |
|
|
|
4 |
) |
2 |
|
|
2 |
1 |
|
|
|
||||||||||||||||||
n→∞ x [0,1] 1+ n |
|
|
ê |
|
|
|
|
|
|
x |
|
|
ú |
n→∞ |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
ëè |
|
|
|
|
|
ø x |
|
|
|
|
|
û |
|
1+ n |
|
× |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n2 |
|
|
|||||||||||||||||||||
Теорема 3.6 (признак Дини для ФП). Пусть |
|
ФП |
|
{ fn (x)} |
||||||||||||||||||||||||||||||||||||
не убывает (или не возрастает) |
в каждой точке сегмента |
|
[a,b] и |
|||||||||||||||||||||||||||||||||||||
сходится на этом сегменте к предельной функции |
f (x). Тогда, если |
|||||||||||||||||||||||||||||||||||||||
все элементы ФП { fn (x)} |
и предельная функция |
f (x) |
непрерывны |
|||||||||||||||||||||||||||||||||||||
на [a,b], то сходимость ФП { fn (x)} является равномерной на [a,b]. З а м е ч а н и е . В теореме 3.6 существенно условие монотонности.
Например, ФП |
fn (x) = |
|
|
nx |
не монотонна на [0,1] (она воз- |
|||||||||||
1 |
+ n2 x4 |
|||||||||||||||
|
|
é |
1 |
ù |
|
é |
1 |
ù |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
растает при |
n £ |
ê |
|
|
ú |
и убывает при |
n > ê |
|
|
ú ) и при этом fn (x) →→ |
0 |
|||||
|
2 |
|
2 |
|||||||||||||
|
|
ë x |
|
û |
|
|
|
|
ë x |
|
û |
[ ] |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
(см. замечание 3 к теореме 3.5).
49
4. Почленное интегрирование |
|
|
|
|
|
|
|
|
|
||||||||||||||||
Теорема 3.7. Если ФП { fn (x)} |
|
сходится равномерно на [a,b] |
|||||||||||||||||||||||
к функции |
|
f (x) , |
а каждая из функций fn (x) |
|
интегрируема на |
||||||||||||||||||||
[a,b] , то предельная функция |
f (x) |
|
интегрируема на [a,b] и |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
x0 [a,b] |
nlim→∞ ò fn (t)dt = ò |
(nlim→∞ fn (t))dt = ò f (t)dt . |
(3.6) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
||
З а м е ч а н и е |
1 . |
В теореме 3.7 существенно условие равномерной |
|||||||||||||||||||||||
сходимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
nx |
|
|
|
® |
|
(см. пример 3.5), но при этом |
|
|
|
|
||||||||||||
1 |
+ n |
2 |
x |
4 |
|
® 0 |
|
|
|
|
|||||||||||||||
|
|
|
|
[ |
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
nt |
|
|
|
æ |
1 |
|
|
1 ö |
1 |
|
p |
|
|
|
ò fn (t)dt =lim |
ò |
|
|
|
arctg(nt) |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
lim |
|
|
|
dt =limç |
|
|
|
0 ÷= |
|
limarctgn = |
|
. |
|||||||||||||
2 |
|
4 |
|
|
|
|
|||||||||||||||||||
n→∞ |
0 |
|
|
|
|
|
|
|
n |
→∞ |
0 |
1+n |
t |
|
|
n→∞ è |
2 |
|
|
ø |
2 n→∞ |
4 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
З а м е ч а н и е |
2 . |
Теорема дает лишь достаточное условие воз- |
|||||||||||||||||||||||
множности почленного интегрирования последовательности. |
|
|
|||||||||||||||||||||||
Ранее было показано (см. пример 3.2), что ФП fn (x) = xn на сегменте [0,1] сходится неравномерно к разрывной функции
( ) ì0, x Î[0,1); f x = íî1, x =1.
Но при этом справедливость равенства (3.6) легко доказать непо- средственным интегрированием.
Теорема 3.8. Если все члены ФП { fn (x)} имеют первообразную
на сегменте [a,b] и fn (x) ® f (x), то функция f (x) также имеет
®
[a,b]
первообразную на [a,b]. Более того, если x0 [a,b], то последова- тельность первообразных Φn (x) функций fn (x), удовлетворяющих условию Φn (x0 ) = 0, сходится равномерно на [a,b] к первообразной Φ (x) функции f (x), удовлетворяющей условию Φ (x0 ) = 0 .
50
5. Почленное дифференцирование
Теорема 3.9. Если ФП { fn (x)} дифференцируемых на [a,b]
функций сходится хотя бы в одной точке x0 [a,b] , а ФП { fn′(x)}
сходится равномерно на [a,b] , то сама ФП { fn (x)} сходится равно- мерно на [a,b] к некоторой дифференцируемой функции f (x) и
x [a,b] f ′(x) = lim fn′(x) .
n→∞
З а м е ч а н и е 1 . В теореме 3.9 под существованием производных подразумевается существование производной на (a,b) , правой про-
изводной в точке a справа и левой производной в точке b слева.
3.4. СХОДИМОСТЬ В СРЕДНЕМ
ФП { fn (x)} интегрируемых с квадратом функций сходится в среднем на [a,b] к интегрируемой с квадратом функции f (x) , если
ε > 0 N = N(ε) n > N òb ( fn (x) − f (x))2 dx < ε,
a
или, что тоже самое,
b
2
limn→∞ òa ( fn (x) − f (x)) dx = 0.
З а м е ч а н и е 1 . Сходимость в среднем также называют средне квадратичной сходимостью.
З а м е ч а н и е 2 . В определении предполагается, что функции fn (x) (n ¥) и функция f (x) интегрируемы с квадратом на [a,b] ,
а значит, и функция
( fn (x)− f (x))2 = fn2 (x) + f 2 (x)− 2 fn (x) f (x)
будет интегрируема на [a,b] .
51
Лемма. Если ФП { fn (x)} сходится в среднем к функции f (x) на множестве A, то эта ФП сходится в среднем к f (x) и на любом множестве B A .
Теорема 3.10. Если ФП { fn (x)} сходится на [a,b] к функции
f (x) равномерно, |
то она сходится к этой же функции в среднем. |
||||||||||||||||
Обратное, в общем случае, неверно. |
|
|
|
|
|
|
|
|
|
||||||||
Так как по условию fn (x)→→ f (x) , то |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
||
|
|
lim sup |
|
fn (x)− f (x) |
|
=0. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
Следовательно, |
n→∞ x [a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 £ limn→∞ òb ( fn (x) - f (x))2 dx = limn→∞ òb |
|
fn (x) - f (x) |
|
2 dx £ |
|
||||||||||||
|
|
|
|||||||||||||||
|
|
|
|||||||||||||||
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||
b |
|
2 |
|
ì |
|
|
|
|
|
|
2 |
|
b |
ü |
|
||
£ lim ò sup |
fn (x) - f (x) |
dx |
|
fn (x) - f (x) |
|
|
= 0. |
||||||||||
|
= lim í sup |
|
|
|
|
òdxý |
|||||||||||
n→∞ a x [a,b] |
|
|
|
|
|
n→∞ îx [a,b] |
|
|
|
|
|
|
|
|
a |
þ |
|
Для доказательства второго утверждения достаточно рассмотреть ФП fn (x) = xn на [0,1]. Ранее было показано, что эта ФП сходится неравномерно к фунции f (x) = 0 на множестве (0,1] [0,1]. Но при
этом она сходится в среднем на |
[ |
] |
к функции |
f |
( |
x |
) |
= 0 : |
|||||
|
0,1 |
|
|
||||||||||
1 |
|
|
1 |
|
x2n |
|
|
1 |
|
|
|
|
1 = 0. |
|
|
|
|
|
|
|
|
||||||
lim ò( fn (x) − f (x))2 dx = lim òx2ndx < |
|
|
|
= lim |
|||||||||
2n |
|
|
|
||||||||||
n→∞ |
n→∞ |
|
|
|
|
|
n→∞ n |
||||||
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
З а м е ч а н и е . |
Если ФП { fn (x)} |
сходится в среднем на [a,b] |
|||||||||||
к функции f (x), то она сходится в среднем на [a,b] |
к любой функ- |
||||||||||||
ции, отличной от |
f (x) не более, чем в конечном количестве точек |
||||||||||||
сегмента [a,b]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
52
Теорема 3.11 |
|
(почленное интегрирование ФП). Если ФП |
|
{ fn (x)} сходится в среднем на [a,b] |
к функции f (x) , то эту после- |
||
довательность можно почленно интегрировать на [a,b] , т.е. |
|||
|
b |
b |
b |
nlim→∞ |
ò fn (x)dx = ònlim→∞ fn |
(x)dx = ò f (x)dx . |
|
|
a |
a |
a |
Доказательство теоремы основано на неравенстве Коши- Буняковского:
|
|
|
|
b |
|
|
|
|
b |
|
b |
|
|
|
|
|
|
|
òh(x) g (x)dx |
|
≤ òh2 (x)dxòg2 |
(x)dx |
|||||||
|
|
|
|
a |
|
|
|
|
a |
|
a |
. |
|
|
|
|
|
|
|
||||||||||
Пусть h(x) = fn (x) − f (x), |
g (x) ≡ 1. Тогда |
|
|
|
||||||||||
|
|
b |
|
b |
|
|
|
b |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
ò fn (x)dx − ò f (x)dx |
= |
ò( fn (x)− f (x))dx |
≤ |
|||||||||
|
|
a |
|
a |
|
|
|
a |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
b |
|
b |
|
|
|
|
b |
|
|
|
|||
≤ ò( fn |
(x) − f (x))2 dxòdx = |
|
(b − a)ò( fn (x) − f (x))2 dx. |
|||||||||||
|
a |
|
a |
|
|
|
|
a |
|
|
|
|||
Так как по условию { fn (x)} |
сходится в среднем на [a,b] к функ- |
|||||||||||||
ции f (x), то
b
lim (b−a)ò( fn (x)− f (x))2dx =0,
n→∞
a
а значит,
|
b |
b |
nlim→∞ |
ò fn (x)dx = ò f (x)dx . |
|
|
a |
a |
53
