Глава 1. ЧИСЛОВЫЕ РЯДЫ

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Элементы теории рядов.pdf

Скачиваний:

Добавлен:

11.03.2016

Размер:

951.2 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Элементы

теории рядов

2014

Содержание
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ ....................................................................	3
Глава 1. Числовые ряды......................................................................................................	4
1.1. Основные определения.........................................................................................	4
1.2. Ряды с неотрицательными членами ....................................................................	9
1.2.1. Признаки сравнения ....................................................................................	10
1.2.2. Интегральный признак Коши – Маклорена..............................................	11
1.2.3. Обобщенный гармонический ряд ..............................................................	12
1.2.4. Признаки Даламбера и Коши .....................................................................	16
1.2.5* Построение новых признаков сходимости ..............................................	19
1.2.6. Отсутствие универсального ряда сравнения ............................................	24
1.3. Ряды общего вида................................................................................................	25
1.3.1. Группировка членов ряда ...........................................................................	25
1.3.2. Ряды лейбницевского типа .........................................................................	26
1.3.3. Абсолютная и условная сходимость..........................................................	27
Глава 2*. Бесконечные произведения .............................................................................	37
Глава 3. Функциональные последовательности ............................................................	43
3.1. Основные определения.......................................................................................	43
3.2. Равномерная сходимость....................................................................................	44
3.3. Свойства равномерно сходящихся последовательностей...............................	47
3.4. Сходимость в среднем ........................................................................................	51
Глава 4. Функциональные ряды.......................................................................................	54
4.1. Основные определения.......................................................................................	54
4.2. Равномерная сходимость....................................................................................	55
4.3. Свойства равномерно сходящихся рядов..........................................................	63
Глава 5. Степенные ряды .................................................................................................	69
5.1. Сходимость степенного ряда .............................................................................	69
5.2. Свойства степенного ряда ..................................................................................	75
5.3. Разложение в степенной ряд ..............................................................................	76
5.4. Равномерное приближение функции многочленами.......................................	86
Глава 6. Тригонометрические ряды Фурье ....................................................................	89
6.1. Периодические функции и их свойства ............................................................	89
6.2. Разложение в ряд Фурье .....................................................................................	90
6.3. Сходимость ряда Фурье......................................................................................	93
6.3.1. Интегральное представление частиной суммы ряда Фурье....................	93
6.3.2. Достаточные условия сходимости ряда Фурье в точке ...........................	96
6.3.3. Характер сходимости рядов Фурье ...........................................................	99
6.4. Операции над рядами Фурье............................................................................	103
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ.......................................................................................	106
ЛИТЕРАТУРА.................................................................................................................	108

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ

Учебное пособие написано на основе курса лекций по математи- ческому анализу, читаемых автором на факультете прикладной математики и информатики НГТУ. Основой для изложения теоре- тического материала послужили следующие издания: «Основы математического анализа» В.А. Ильина и Э.Г. Позняка, «Курс мате- матического анализа» Л.Д. Кудрявцева и «Задачи и упражнения по математическому анализу» И.А. Виноградовой.

Пособие охватывает основные разделы теории числовых и функциональных рядов. Оно содержит все необходимые для изуче-

ния курса определения и теоремы и может быть использовано как для самостоятельного изучения курса, так и в качестве расширенно- го конспекта лекций.

Весь теоретический материал проиллюстрирован примерами, раскрывающими его суть и облегчающими восприятие курса в целом. Изложение математического анализа ведётся на уровне, доступном широкому кругу студентов. Материал, помеченный знаком «*»,

является в некотором роде дополнительным и предназначен для более глубокого изучения. Как правило, это разделы математиче- ского анализа, не обязательные для базового курса. При первом (ознакомительном) прочтении глав пособия указанные разделы

рекомендуется пропускать и возвращаться к ним только после разбора основной части материала по данной теме.

Автор выражает глубокую благодарность студентам факультета ФПМИ А.Н. Игнатьеву и Д.В. Шилаку за активную помощь в создании данного учебного пособия.

< q + e =1- e,

1.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Пусть задана некоторая числовая последовательность a1,a2 ,K,ak ,K

Формально образованное из элементов этой последовательности выражение вида

∞
a1 + a2 + ...+ ak + ... = åak	(1.1)

k=1

называют числовым рядом, а входящие в него слагаемые – членами числового ряда.

Сумму первых n членов данного ряда называют частичной суммой ряда и обозначают Sn :

∞	∞
а ряд rn = åan+k =	å ak
k=1	k=n+1

Sn = åak ,

k=1

∞

называют n -м остатком ряда åak .

k=1

Ряд (1.1) называется сходящимся, если последовательность {Sn}

частичных сумм этого ряда имеет конечный предел S , при этом S называют суммой данного ряда. Таким образом, для сходящегося

ряда формально можно записать

∞

S = åak ,

k =1

где S = lim Sn .

n→∞

Если последовательность {Sn} частичных сумм ряда расходится, то ряд называется расходящимся.

З а м е ч а н и е 1. Понятие «сумма ряда» определено только для сходящегося ряда и в отличие от понятия «частичная сумма ряда» вводится посредством предельного перехода.

З а м е ч а н и е 2. Если ряд (1.1) имеет сумму S , то верно равен- ство S = Sn + rn , из которого следует, что остаток сходящегося ряда

rn равен погрешности замены суммы ряда S частичной суммой Sn .

Изучение числовых рядов есть новая форма изучения числовых последовательностей, так как:

1)каждому ряду однозначно соответствует последовательность его частичных сумм;

2)каждой данной последовательности {Sn} однозначно соответ-

ствует ряд, для которого эта последовательность является последо- вательностью частичных сумм:

a1 = S1; k >1 ak = Sk − Sk−1.

Следующие примеры показывают взаимосвязь понятий ряда и последовательности, суммы ряда и предела последовательности.

П р и м е р 1.1. Исследуем сходимость геометрического ряда

			∞
			åqk−1 .
			k=1
1. При q =1 очевидно, что lim Sn				= +∞ .
			n→∞
2.	При q = −1 S2m−1 =1, S2m = 0 m , поэтому последовательность
Sn не имеет предела при n → ∞ .
3.	При	q	¹1 частичная сумма	Sn этого ряда вычисляется

по формуле суммы членов геометрической прогрессии:

Sn =

1- qn

1- q

Следовательно, при

<1 lim S

, а при

>1 lim S

= ∞ .

1- q

n→∞

∞

Таким образом, ряд

åqk−1

при

<1 сходится к числу

1- q

∞

k=1

т.е. åqk−1 =

, а при

³1 – расходится.

1− q

k =1

∞

П р и м е р 1.2. Исследуем сходимость ряда å

k (k +1)

k 1

Вычислим частичную сумму этого ряда:

1 ù é1

ù é

1ù é1

Sn = å

ú = ê

+ ê

ú + ê

+... =1-

n +1

k=1

ëk

k +1û ë1

û ë

3û ë3

Так как lim Sn

= 1, данный ряд сходится к 1.

n→∞

В приведенных примерах последовательность {Sn} частичных

сумм соответствующего ряда выражалась достаточно просто, так что существование и величина предела Sn устанавливались непо-

средственно. Обычно такой анализ последовательности {Sn} невоз-

можен, поэтому основными задачами в теории числовых рядов

являются установление сходимости или расходимости данного ряда без вычисления его частичных сумм и оценка зависимости величи-

ны остатка rn от номера n (скорость сходимости ряда).

Критерий Коши сходимости ряда

Так как вопрос о сходимости ряда по определению эквивалентен вопросу о сходимости последовательности его частичных сумм,

можно получить необходимое и достаточное условие сходимости данного ряда, сформулировав критерий сходимости Коши для последовательности его частичных сумм.

∞

Теорема 1.1 (критерий Коши). Для того чтобы ряд åak

k=1

сходился, необходимо и достаточно, чтобы

		n+ p
		n+ p
"e > 0	$n0 "n ³ n0 "p	å ak	< e .
		k =n+1

Для доказательства достаточно заметить, что

n+ p

å ak = Sn+ p − Sn . k=n+1

З а м е ч а н и е . Критерий сходимости Коши представляет в основ- ном теоретический интерес и редко используется для доказатель- ства сходимости конкретных рядов из-за технических трудностей.

П р и м е р 1.3. Пользуясь критерием Коши, докажем расходимость

		∞	1	. Ряд расходится, так как
гармонического ряда å			1	. Ряд расходится, так как
		k=1	k
	1					2n		1
						2n
$e =		"n0		$n = n0	$p = n	å 1	³		n =	1 .
$e =	2	"n0		$n = n0	$p = n	å 1	³	2n	n =	1 .
	2					k=n+1 k		2n		2

		∞
Теорема 1.2. Если ряд åak			сходится, то последовательность
	∞	k=1
	∞
остатков ряда rn	= å ak является бесконечно малой.
	k=n+1
	∞
Пусть S = åak		= lim Sn . Тогда
	k=1	n→∞
limrn = lim(S - Sn ) = S - lim Sn = S - S = 0				.
n→∞	n→∞		n→∞

Теорема 1.3 (необходимое условие сходимости ряда). Для схо-

∞

димости ряда åak необходимо, чтобы

k=1

lim ak

= 0.

(1.2)

∞

k→∞

ak = Sk − Sk−1 , то

Пусть S = åak = lim Sn . Так как k >1

k=1

n→∞

lim a

= lim(S

- S

k−1

) = lim S

- lim S

k−1

= S - S = 0

k→∞ k

k→∞

З а м е ч а н и е . Гармонический ряд – это пример расходящегося ряда, для которого выполнено условие (1.2), следовательно, это условие не является достаточным для сходимости ряда.

	∞
П р и м е р	1.4. Ряд åsin k	расходится, так как предел ak = sin k
	k=1	т.е. нарушено необходимое условие
при k → ∞ не существует,
		∞
сходимости.	Доказанная ранее расходимость ряда åqk−1 ,		q	³1,

k=1

также может быть обоснована невыполнением необходимого усло- вия сходимости.

Основные свойства сходящихся рядов

1. Отбрасывание или добавление конечного числа членов не вли- яет на сходимость ряда.

∞
2. Если c ¹ 0 , то ряд å(cak )	сходится тогда и только тогда, когда
k=1	∞	∞
∞
сходится ряд åak , причем в случае сходимости å(cak ) = cåak .
k=1	k =1	k=1

∞		∞	∞
3. Если ряды åak и åbk сходятся, то сходится ряд å(ak ± bk ),
k=1		k=1	k =1	∞
∞	∞	∞	∞	∞
причем å(ak ± bk )	= åak ± åbk		. Если один из рядов åak	и åbk
k =1	k =1	k=1	k=1	k=1
			∞
сходится, а второй расходится,			то ряд å(ak ± bk ) расходится. Если
∞	∞		k =1
∞	∞		∞
оба ряда åak и	åbk	расходятся, то ряд å(ak ± bk ) может как
k=1	k=1		k =1

сходиться, так и расходиться.

Доказательства этих свойств основаны на использовании соответствующих свойств числовых последовательностей.

З а м е ч а н и е . Согласно свойству 1 всюду в формулировках условий сходимости или расходимости ряда можно требование «для всех членов ряда» заменить требованием «для всех членов ряда, начиная с некоторого номера». В дальнейшем такая замена будет подразумеваться без специальной оговорки.

						∞	3k + 5k
П р и м е р 1.5. Ряд знакопостоянный å							20	k	сходится, так как
						k=1	20
∞ æ	3	ök	∞ æ	1	ök
каждый из рядов åç		÷	и åç		÷	сходится (см. пример 1.1).
каждый из рядов åç	20	÷	и åç	4	÷	сходится (см. пример 1.1).
k =1 è	20	ø	k=1 è	4	ø

∞

20k + 5k k

∞

1 ök

П р и м е р 1.6. Ряд å

расходится, так как ряд åç

∞

k=1

расходится (см. пример 1.3).

сходится, а ряд å

k=1

∞

П р и м е р 1.7. Ряд å

сходится (см. пример 1.2), хотя

k (k +1)

k 1

∞

∞ æ 1

= åç

k (k +1)

k +1

k 1

k 1 è k

∞

и оба ряда å1

, å

= å

расходятся.

k +1

k=1 k

k =1

k=2

1.2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ

∞

Рассмотрим знакопостоянные ряды, т.е. ряды åak такие, что

k=1

k ak ³ 0 или ak £ 0. С учетом свойства 2 сходящихся рядов можно

ограничиться рассмотрением только рядов с неотрицательными членами. Те случаи, когда неравенство ak ³ 0 необходимо заменить неравенством ak > 0, будем оговаривать особо.

Теорема 1.4 (основное свойство рядов с неотрицательными членами). Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.

Очевидно, что последовательность частичных сумм ряда с неотрицательными членами является неубывающей, а для неубы- вающей последовательности ее сходимость и ограниченность экви- валентны.

			∞
Теорема 1.5. Если знакопостоянный ряд åak сходится, а после-
			k=1
			∞
довательность {dk }	ограничена, т.е. n	dn	≤ L, то ряд åak dk также
довательность {dk }	ограничена, т.е. n	dn	≤ L, то ряд åak dk также

k=1

сходится.

Для доказательства используем критерий Коши. Пусть после-

довательность {dk } ограничена числом

L .

Пусть

ε > 0, тогда из

∞

сходимости ряда åak получим, что

k=1

n+ p

$n0 "n ³ n0 p

å ak

следовательно,

k=n+1

≤ å ak dk

≤ L å ak = L

å ak < L ε = ε.

å ak dk

n+ p

k=n+1

k =n+1

k=n+1

1.2.1. Признаки сравнения

∞

Теорема 1.6 (первый признак сравнения). Пусть ряды åak и

∞				k=1
∞				∞
åbk таковы,		что k 0 ≤ ak ≤ bk . Тогда из сходимости ряда åbk
k=1		∞	∞	k=1
		∞	∞
следует сходимость ряда åak , а из расходимости ряда åak				следу-
		k=1	k=1
		∞
ет расходимость ряда åbk .
		k=1
Пусть	An	и Bn – соответствующие n -е частичные суммы ря-
дов, тогда	An	≤ Bn . Следовательно, ограниченность	{Bn}	влечет

ограниченность { An} , а неограниченность { An} влечет неограни- ченность {Bn} . Отсюда с учетом теоремы 1.4 получаем требуемое утверждение.

Следствие. Теорема остается справедливой, если неравенство

0 ≤ ak	≤ bk заменить неравенством 0 ≤ ak ≤ cbk , c ¡+ , так как ряды
∞	∞
åcbk	и åbk сходятся и расходятся одновременно.
k=1	k=1
			∞
Теорема 1.7 (второй признак сравнения). Пусть ряды åak и
∞		k=1
∞			ak
åbk	таковы, что k ak > 0, bk > 0 и существует предел lim		ak	= c ,
åbk	таковы, что k ak > 0, bk > 0 и существует предел lim			= c ,
k=1		k→∞ b
k=1			k
0 ≤ c ≤ +∞ . Тогда если:
	∞
1)	0 ≤ c < +∞ , то из сходимости ряда åbk следует сходимость
	k=1
	∞
ряда åak ;
k=1
	∞
2)	0 < c ≤ +∞ , то из расходимости ряда åbk следует расходи-

k=1

∞

мость ряда åak ;

k=1

3)0 < c < +∞ , то оба ряда сходятся и расходятся одновременно.


∞		ak
1. Пусть 0 ≤ c < +∞ и ряд åbk сходится. Положим dk	=	ak		.
1. Пусть 0 ≤ c < +∞ и ряд åbk сходится. Положим dk	=			.
k=1		bk	}
Очевидно, что k dk > 0. По условию последовательность	{dk		}

имеет конечный предел c , а значит, ограничена. В силу теоремы 1.5

				∞		∞	∞
из сходимости ряда åbk следует сходимость ряда åbk dk = åak .
				k=1		k =1	k=1
					∞
2.	Пусть 0 < c ≤ +∞ и ряд åbk расходится. Предположим, что
	∞				k=1
	∞
ряд åak сходится.					Тогда, введя в рассмотрение последователь-
k=1
ность	dk =	bk	( k	dk	> 0) и повторив рассуждения из предыдущего
ность	dk =		( k	dk	> 0) и повторив рассуждения из предыдущего
		ak			∞	∞
					∞	∞
пункта, получим,				что ряд åbk		= åak dk сходится, что противоре-
					k =1	k=1
						∞
чит условию. Следовательно, ряд åak расходится.

k=1

3.Утверждение является следствием первых двух.

З а м е ч а н и е .

Согласно

второму

признаку

сравнения,

если

∞

ak : bk при

k → ∞,

то ряды

åak и

åbk сходятся и расходятся

одновременно.

k=1

Теорема

1.8

(третий

признак

сравнения).

Пусть

ak+1

bk+1

∞

ak > 0, bk > 0

≤

. Тогда из сходимости ряда åbk

следует

k=1

∞

сходимость ряда

åak , а из расходимости ряда

åak

–

расходи-

∞

k=1

мость ряда åbk .

k=1

Положим dk = ak . Тогда из условия теоремы bk

k 0 < dk+1 = ak+1 ≤ ak = dk . bk+1 bk

Следовательно,	последовательность	{dk }	– невозрастающая,
			∞	∞
ограниченная, поэтому в силу теоремы 1.5 ряд åak = åbk dk схо-
дится.			k =1	k=1
дится.		∞
		∞
Утверждения «из сходимости ряда		åbk	следует	сходимость
∞		k=1
∞		∞
ряда åak » и «из расходимости ряда åak следует расходимость
k=1	k=1
∞
ряда åbk » эквивалентны, поэтому можно			считать,	что теорема

k=1

доказана полностью.

1.2.2. Интегральный признак Коши – Маклорена

Теорема 1.9 (интегральный признак Коши – Маклорена).

Пусть f (x) ³ 0 и не возрастает всюду на полупрямой x ³ m . Тогда

∞

для сходимости числового ряда å f (k ) необходимо и достаточно

k=m

существование конечного предела при n → ∞ последовательности

an = òn	f (x)dx		(1.3)
m		+∞
		+∞
или, что то же самое, сходится несобственный интеграл		ò	f (x)dx.
Пусть k ³ m +1, xÎ[k -1,k]. Тогда		m
Пусть k ³ m +1, xÎ[k -1,k]. Тогда
f (k ) £ f (x) £ f (k -1).			(1.4)

Так как функция f (x) на сегменте [k -1,k] ограничена и не возрас- тает, то она интегрируема на [k -1,k]. Учитывая свойства интегра- лов, из (1.4) получим

f (k ) = òk	f (k )dx £ òk	f (x)dx £ òk	f (k -1)dx = f (k -1).
k−1	k−1	k−1
Сложив эти неравенства для k = m +1,m + 2,K,n, получим
	n	n	n−1
	å f (k )	£ ò f (x)dx £	å f (k ).	(1.5)
	k=m+1	m	k=m

n
Обозначим Sn = å f (k ). Тогда учитывая (1.3), можно записать
k=m
(1.5) в виде:
Sn − f (m) ≤ an ≤ Sn−1 .	(1.6)

Из условия теоремы следует, что последовательность {an} не убы-

вает, поэтому для ее сходимости этой необходимо и достаточно ее ограниченности. Из неравенств (1.6) вытекает, что последователь- ность {an} ограничена тогда и только тогда, когда ограничена после-

довательность {Sn} , что эквивалентно ее сходимости.

Следствие. Пусть f (x) удовлетворяет условиям теоремы, а ряд

∞

å f (k ) сходится, тогда остаток ряда можно оценить по формуле

k=m

∞

ò f

(x)dx ≤ rn0 ≤ ò f (x)dx , rn0 = å f (k )

n0 +1

k=n0 +1

Неравенство (1.5) можно записать в виде

n−1

å f

(k ) ≤ ò f (x)dx ≤

f (k ) ≤ ò f (x)dx .

k=n0 +2

n0 +1

k=n0 +1

Переходя к пределу при n → ∞ , получим требуемую формулу.

1.2.3. Обобщенный гармонический ряд

Теорема 1.10. Обобщенный гармонический ряд

∞

(1.7)

åk =1 kα

сходится при α >1 и расходится при α ≤1.

Обобщенный гармонический ряд (1.7) можно рассматривать

∞

как ряд вида å f (k ), если положить

m =1, f (x) =

. Функция

xα

(

)

k=m

[

)

убывает и положительна на

1,+∞

, поэтому в силу признака

Коши – Маклорена вопрос о сходимости ряда (1.7) эквивалентен

вопросу о сходимости несобственного интеграла	∞ò	1	dx , который
		α
сходится при α >1 и расходится при α ≤1.	1	x

∞	1
П р и м е р 1.8. Найдем сумму ряда å		с точностью до 10−2 .
	4
k=1	k

Задача корректна, так как данный ряд сходится, поэтому, согласно интегральному признаку Коши, получим

+∞ dx

rn = S - Sn £

òn x4

3n3

Так как r £10−2

при

n ³ 4,

для

вычисления ряда с заданной

погрешностью достаточно взять

=1+

Обобщенный гармонический ряд часто используется при иссле- довании сходимости рядов с помощью теорем сравнения.

П р и м е р 1.9. Исследуем сходимость ряда

∞ æ

k + 2

åçexp í

-1÷ .

k =1 ç

ï k

+ 2

Так как

® 0 при k ® ¥, то

ì 3

k + 2

+ 2

при k ® ¥.

exp

ý -1

k2 + 3

k5/ 3

В силу второго признака сравнения с учетом сходимости обоб- щенного гармонического ряда при α = 53 получаем сходимость

исходного ряда.

Элементарные функции – показательная ex и логарифмическая

ln x – при	x → +∞ не являются		бесконечно большими степенного
порядка, а	именно для	любого	a > 0 справедливы соотношения
xα = o(ex )	и ln x = o(xα ),	x → +∞ . Иногда возможно получить оцен-

ку общего члена такого ряда через степенную функцию и, пользуясь теоремой сравнения, сделать вывод о поведении этого ряда.

∞

П р и м е р 1.10. Исследуем сходимость ряда åk2e− k .

									k =1
Функция e−		убывает					быстрее,		чем любая отрицательная
Функция e−	k	убывает					быстрее,		чем любая отрицательная
				e−				= o(k−α / 2 ) при k → ∞ (α > 0). Если
степень показателя			, т.е.				k
степень показателя		k	, т.е.				k
∞
α0 > 6 , то ряд åk2−α0 / 2 сходится, а значит, в силу теоремы сравнения
k=1
сходится и исходный ряд.
З а м е ч а н и е . Оценка e−						= o(k−α / 2 )			верна и для 0 < α0 < 6, но
З а м е ч а н и е . Оценка e−					k	= o(k−α / 2 )			верна и для 0 < α0 < 6, но

∞

такая оценка не информативна в вопросе о сходимости ряда åk2e− k .

						k =1
				∞
П р и м е р 1.11*. Исследуем сходимость ряда å					ln k	, q > 0 .
П р и м е р 1.11*. Исследуем сходимость ряда å					q	, q > 0 .
				k =1 k
Из неравенства	ln k	>	1	, k > 3, q > 0 , в силу теоремы сравне-
Из неравенства	kq	>	kq	, k > 3, q > 0 , в силу теоремы сравне-
	kq		kq

ния следует, что данный ряд расходится при 0 < q ≤1. Пусть q >1. Так как α > 0 ln k = o(kα ) при k → ∞, для каждого α > 0 найдется номер K (α) такой, что для всех k > K (α)

ln k	<	1	.			(1.8)
kq
		kq−α
			∞		1
Обобщенный гармонический ряд å						сходится при q − α >1,
				k	q−α
		k=1

поэтому, выбирая для каждого фиксированного значения q >1 зави-

сящее от него значение α =					q −1		, получим, что k > K (α) справед-

		2
ливо неравенство		(1.8). Отсюда в силу теоремы сравнения 1.6
			∞
делаем вывод, что ряд å				ln k		сходится.
				q
			k =1 k
∞
Итак, ряд å	ln k		сходится при q>1 и расходится при 0< q≤1.
	q
k =1 k

1.2.4. Признаки Даламбера и Коши

Эти признаки сходимости основаны на сравнении рассматривае- мого ряда с рядом, составленным из элементов геометрической

∞

прогрессии, а именно со сходящимся рядом åqk ,

<1 или расхо-

∞

k =1

дящимся рядом å1.

k =1

Теорема 1.11 (признак Даламбера). Если k

ak > 0 и справед-

ak+1

∞

ливо неравенство

£ q <1 (или

³1),

то ряд åak

сходится

(расходится).

k=1

Пусть b = qk

=1). Тогда

bk+1

= q <1

bk+1

=1ö.

Из условия теоремы получим

è bk

ak+1

£ q =

bk+1

ak+1

³1 =

bk+1

(1.9)

è ak

∞

Так как ряд åbk = åqk , q <1, сходится ç

åbk =

å1 расходится÷ ,

k=1

è k=1

k=1

на основании 3-го признака сравнения получаем, что неравенства

∞

(1.9) гарантируют сходимость (расходимость) ряда åak .

k=1

З а м е ч а н и е .

Неравенство

ak+1

£ q <1 нельзя заменить неравен-

∞ 1

ством

k+1

<1. Например, ряд

å k

расходится, хотя

k+1

<1.

k +1

k=1

Теорема 1.12 (признак Даламбера в предельной форме). Пусть

k ak > 0 и lim

ak+1

= q Î¡.

k→∞ a

∞

Тогда

ряд

åak

сходится

при

q <1

и расходится

при q >1.

k=1

При q =1 ряд может как сходиться, так и расходиться.

Если q <1, то ε > 0 q =1− 2ε и q + ε =1− ε . По определению предела последовательности для указанного ε

∞

значит, ряд åak

k=1

сходится (по признаку Даламбера).

Если q >1, то ε > 0 q =1+ ε и q − ε =1. По определению преде- ла последовательности для указанного ε

$k0 "k ³ k0 1 = q - e < aak +1 ,

∞

значит, ряд åak расходится (по признаку Даламбера).

∞

k=1

∞

Ряд å

сходится, а гармонический ряд å1

расходится, хотя

k=1

k=1 k

для каждого из них q =1.

Теорема 1.13 (обобщенный признак Даламбера). Пусть k

ak > 0. Тогда, если:

ak+1

∞

lim

= L <1, то ряд åak

сходится;

→∞

k=1

ak+1

∞

2) lim

= L >1, то ряд åak

расходится.

k→∞

k=1

k ak ³ 0 и

Теорема 1.14 (радикальный признак Коши). Если

справедливо неравенство

£ q < 1 ( k

³1),

(1.10)

∞

то ряд åak сходится (расходится).

k=1

= qk

=1), то из неравенств (1.10) получим:

Если положить b

∞

теорема сравнения

£ q < 1 Þ ak

£ bk

сходимость ряда åak .

k=1

теорема сравнения

∞

³1 Þ ak ³ bk

расходимость ряда

åak .

З а м е ч а н и е . Как

признаке Даламбера,

k=1

неравенство

kak £ q < 1 нельзя заменить неравенством kak <1.

Теорема 1.15 (радикальный признак Коши в предельной

форме). Если k a	k	³ 0	и существует предел lim k	a	= q, то ряд
	k		k→∞	k
∞			k→∞
∞
åak сходится при	q <1		и расходится при q >1. При q =1 ряд

k=1

может как сходиться, так и расходиться.

Доказательство совпадает с доказательством признака Даламбера

в предельной форме, если в рассуждениях заменить ak+1 на k ak . ak

Теорема 1.16 (обобщенный радикальный признак Коши).

					∞
Если k ak ³ 0 и существует предел	lim	k	ak	= q , то ряд	åak
k→∞					k=1
сходится при q <1 и расходится при q >1.					k=1
сходится при q <1 и расходится при q >1.

З а м е ч а н и е 1. Признаки Коши и Даламбера

– применимы только для рядов с неотрицательными членами;

– являются достаточными и не являются необходимыми.

З а м е ч а н и е 2. Так как для частичных пределов последователь-

ности с положительными членами справедливо неравенство

lim

ak+1

£ lim k

ak+1

lim

k→∞ a

k→∞

k→∞ a

признак Коши является более сильным, чем признак Даламбера, т.е. всякий раз, когда действует признак Даламбера, действует и признак Коши. При этом существуют ряды, для которых действует признак Коши и не действует признак Даламбера.

∞

(-1)

+ 3

Например, для ряда å

имеем

k=1

2n 1 1

1+ 3

22n−1

lim

= lim

(

− )+

= lim

22n

=1,

-1+ 3

k→∞

n→∞

(2n−1)

-1+ 3

22n

lim

= lim

2n+1

= lim

22n+1

1+ 3

k→∞

n→∞

следовательно, признак Даламбера не дает информации ни о сходи- мости, ни о расходимости данного ряда, тогда как признак Коши

доказывает сходимость ряда		k		= lim 2n		=	1	.
	lim		ak		a2n
	k→∞			n→∞			2

1.2.5. Построение новых признаков сходимости*

Малая чувствительность признака сходимости Даламбера объяс- няется тем, что он основан на сравнении исследуемого ряда с таким резко расходящимся рядом, как арифметическая прогрессия, или же с таким быстро сходящимся рядом, как геометрическая прогрессия.

Поэтому естественно попытаться построить признаки сходимости рядов, основанные на сравнении их членов с членами рядов, сходя- щихся или расходящихся медленнее, чем указанные ранее (доказа- тельство существования таких рядов приведено выше).

Теорема 1.17 (признак Куммера). Пусть даны расходящийся

∞

ряд å

и последовательность {ak }, k

ak > 0, ck > 0. Обозначим

k=1 k

через Kk

величину

= c

- c

(1.11)

k a

k+1

Тогда, если k выполняется неравенство Kk ³ d > 0:

∞

³ d > 0, то ряд åak

сходится;

∞

k=1

£ 0 , то ряд åak

расходится.

k=1

Пусть k

= c

- c

³ d > 0. Умножив

обе

части

k+1

этого неравенства на ak+1 , получим

ck ak

- ck+1ak +1 ³ dak+1 ,

(1.12)

значит, ck ak - ck +1ak+1 > 0. Отсюда вытекает, что величина ck ak

моно-

тонно убывает и, следовательно, стремится к

конечному

пределу (так как она ограничена снизу нулем).

∞

− ck +1ak+1 )

Итак,

ряд å(ck ak

сходится,

так как сумма его n пер-

k=1

вых членов c1a1 - cn+1an+1 имеет конечный предел. Но тогда из нера- венства (1.12) в силу теоремы сравнения следует, что сходится ряд

∞	∞
åδak	, а с ним и исходный ряд åak .
k=1	k=1

2. Пусть k

= c

- c

£ 0 . Тогда

ak+1

1/ ck+1

. Так как

1/ c

k+1

∞

k+1

ряд å

предположен расходящимся, согласно теореме сравнения,

k=1 k

∞

то расходится и ряд åak .

k=1

Следствие (признак Куммера в предельной форме). Допу-

	стим, что предел lim Kk = K . Тогда при K > 0 ряд	∞
	стим, что предел lim Kk = K . Тогда при K > 0 ряд	åak сходится,
	k→∞	k=1
	а при K < 0 – расходится.	k=1
	а при K < 0 – расходится.

Признак Куммера можно рассматривать как общую схему для получения конкретных признаков. Выбирая различным образом

∞
расходящийся ряд åc1 , мы будем получать различные признаки
k=1	k

сходимости. Продемонстрируем такой способ построения призна- ков на следующих примерах.

Признак Даламбера. Положив в формуле (1.11) ck =1, получим

-1 =

-1,

ak+1

где

D =

ak+1

. Если lim D = D , то

lim K

−1. При D >1

имеем

k→∞

K < 0 , и по

признаку

Куммера

ряд

расходится; если же

D <1,

то K > 0 , и ряд сходится.

Признак Раабе. Положив в формуле (1.11) ck = k , получим

= k

-(k +1) = Rk -1,

ak+1

æ	ak	ö		lim Rk = R , то	lim Kk = R −1. При
где Rk = k ç		-1÷	. Если

è ak+1		ø		k→∞	k→∞

имеем K < 0 , и по признаку Куммера ряд расходится; если же то K > 0 , и ряд сходится.

R <1

R >1,

Признак Бертрана. Положим в формуле (1.11)

ck = k ln k . Расхо-

∞

димость ряда å

вытекает из интегрального признака Коши –

k=1 k

Маклорена. Выражение для Kk в этом случае примет вид:

= k ln k ×

- (k +1)ln(k +1) =

ak+1

= ln k ék

-1ö

-1ù

- ln æ1+

1 ök+1 = B - ln

æ1+

1 ök+1 ,

è ak+1

k ø

é æ

(Rk -1).

где Bk = ln k

êk ç

1÷ -1ú = ln k

ë è ak+1

Если lim Bk

= B , то lim Kk = B −1. При B <1 имеем K < 0 , и по

k→∞

→∞

B >1, то K > 0 , и ряд

признаку Куммера ряд расходится; если же

сходится.

Докажем теперь несколько признаков, основанных на тех, что

построены ранее.						ak
Признак Гаусса. Допустим, что соотношение						ak	может быть
Признак Гаусса. Допустим, что соотношение						a	может быть
						a
	ak	= l + m	+ qk ,			k+1
представлено в виде	ak			где	λ и	μ –	постоянные,
представлено в виде	a			где	λ и	μ –	постоянные,
	a	k	k2
	k+1
а θk – ограниченная величина. Тогда,				если	λ >1 или		λ =1, μ >1,

∞

то ряд åak сходится; если λ <1 или λ =1, μ ≤1, то он расходится.

k=1

Случаи λ >1 и λ <1 приводят к признаку Даламбера, так как

lim D =			1	.
lim D =				.
k→∞	k		l
	Если λ =1, то R = m +				qk	и R = μ , а значит,				случаи μ >1 и μ <1
	Если λ =1, то R = m +					и R = μ , а значит,				случаи μ >1 и μ <1
				k
исчерпываются признакомkРаабе.
	Если		λ =1, μ =1, то имеем B = ln k q					k	и	lim B = 0 , так как
						k	k	k		k→∞	k
lim ln k							k			k→∞
lim ln k		стремится к 0 при k → ∞, а величина θk								ограничена. Следо-
k→∞	k
вательно, по признаку Бертрана ряд расходится.

Логарифмический признак. Если существует конечный или

бесконечный предел

limç k ln

÷ = r, - ¥ £ r £ +¥

∞

k→∞ è

ak+1 ø

то ряд åak

сходится, если r > 1, и расходится, если r < 1.

k=1

Доказательство основано на использовании неравенств

< ln

ç1+

(1.13)

k +1

1. Пусть r > 1, 1< ρ < r

– фиксировано. По определению предела

последовательности

$k0

"k ³ k0

k ln

³ r или ln

³ r .

(1.14)

ak+1

Учитывая (1.13), из (1.14) получим

æ k

(

k +1

)

> rln ç1+

ak+1

è k

∞

kρ

Так как обобщенный гармонический ряд å

сходится при ρ >1,

k =1

∞

по третьему признаку сравнения сходится и исходный ряд åak .

k=1

2. Если r < 1, то по определению предела последовательности

$k0	"k ³ k0	k ln	ak	£1.

			ak+1

Учитывая (1.14), получим

< lnç1

ak+1

k -1

ak+1

k -1

Следовательно, по признаку сравнения исходный ряд расходится.

П р и м е р 1.12. Исследуем сходимость ряда

å(

2k −1)!!

1 .

∞

k 1 (2k )!!

2k +1

Рассмотрим отношение

(

)

(

k+1

)

(

)(

)

2k + 2

)(

2k + 2

2k + 3

!! 2k + 3

2k -1 !!

(

2k +1 !! 2k

!! 2k +1

)

(

) (

)

(

)

Поскольку

lim

=1,

для

решения

вопроса о

сходимости

k→∞ a

данного ряда метод Даламбера неприменим. Воспользуемся мето-

дом Гаусса:

+10k + 6

=1+

6k + 5

=1+ 3 k −

4k2

+ 4k +1

4k2 + 4k +

4k2 + 4k +1

k+1

=1+

k + Oç

÷ при k → ∞.

è k

Поскольку λ =1 и μ =

>1, рассматриваемый ряд сходится.

П р и м е р 1.13. Исследуем сходимость ряда

∞

åk 1

, α > 0.

(a +1)(a + 2)L(a + k )

Так как

lim

= lim a +1+ k

=1,

k→∞ a

k→∞

k +1

k+1

метод Даламбера неприменим для решения вопроса о сходимости данного ряда. Воспользуемся в данном случае методом Гаусса:

a +1+ k

a / k

æ 1 ö

при k → ∞.

=1+

+ Oç

ak+1

k +1

è k

при α >1 и

Таким образом,

рассматриваемый

ряд сходится

расходится при α ≤1.

1.2.6. Отсутствие универсального ряда сравнения

Признаки Коши и Рабе сильнее признака Даламбера. Признак Бертрана сильнее признака Раабе. Эта цепь все более и более чувствительных (но и более сложных) признаков может быть неограниченно продолжена. Возникает вопрос: существует ли сходящийся (или расходящийся) ряд, сравнение с кото- рым позволило бы сделать заключение о сходимости (или расходимости) любо- го наперед взятого знакопостоянного ряда.

∞

Ряд åa%k

называется

сходящимся

(расходящимся)

медленнее,

чем

k =1

∞

ряд åak , если

lim

= 0

çlim

= 0÷,

где символами rn

и r%n ( Sn и

S%n )

k =1

n→∞ r%

n→∞ S

обозначены соответственно их n -е остатки (частичные суммы).

Теорема 1.18. Для каждого сходящегося (расходящегося) ряда существует ряд, сходящийся (расходящегося) медленнее этого ряда.

∞

Пусть

åak

–

сходящийся ряд.

Тогда

ряд

å(

−

rk −1

∞

k =1

∞

k=1

∞

где r0

= åak ,

rk = åan

сходится медленнее, чем ряд åak , так как

k =1

n=k

k =1

r%n =(

−

(

−

)+ ...=

lim

=lim

=0.

rn 1

n→∞ r%

n→∞

∞

Пусть åak

–

расходящийся ряд,

– его

n -я частичная сумма. Тогда

k =1

∞

ряд

+ å(

−

), сходится медленнее, чем ряд åak

, так как

Sk −1

k =2

k =1

S%n =

+ (

−

)+ ...+ (

−

) =

и lim S%n

= lim

1 = 0.

Sn 1

−

n→∞ Sn

n→∞

Следствие. Никакой сходящийся (расходящийся) ряд не может служить «универсальным рядом», сравнение с которым устанавливает сходимость (расходимость) произвольного знакопостоянного ряда.

∞

Пусть åak

– сходящийся ряд, то ряд åa%k = å(

−

) сходится,

rk −1

k =1

rk −1

− rk

k =1

>> a

(

→ 0).

хотя

k−1

a%k

− r

k −1

∞

k −1

∞

Если

åak

–

расходящийся

ряд,

то ряд

åa%k =

+ å (

−

Sk −1

)

k =1

k=1

k =2

Sk − Sk

расходится, хотя

- Sk−1 <<ak

(

= Sk

+ Sk −1 →∞ ).

a%k

−

Sk −1

1.3.РЯДЫ ОБЩЕГО ВИДА

Вэтой главе мы откажемся от введенного ранее условия знако- постоянности ряда и будем рассматривать как знакопостоянные, так и знакопеременные ряды.

1.3.1.Группировка членов ряда

				∞
Пусть дан ряд				åak . Сгруппировать члены этого ряда – это
				k=1		∞		Nk −1
				∞		∞		Nk −1
значит вместо ряда				åak рассмотреть ряд åAk ,			где	Ak = å an ,
1 = N		< N < ... < N		k=1	, т.е. A	k=1	есть	n=Nk 1
1 = N	0	< N < ... < N	k	< ...	, т.е. A	для каждого k	есть	сумма − k -й
	0	1	k		k

группы (скобки) членов ряда. Пусть Sn – частичные суммы ряда

∞	и S%n				∞
åak	и S%n	– частичные суммы ряда			åAk . Для конечных сумм
k=1					k=1
раскрытие скобок законно, поэтому
S%n	n	N1−1	N2 −1	Nn −1	= a1 + a2 + ...+ aNn −1 = SNn −1,
S%n	= å Ak	= åak + å ak + ...+		å ak	= a1 + a2 + ...+ aNn −1 = SNn −1,
	k =1	k=1	k =N1	k =Nn−1

т.е. последовательность {S%n } – это подпоследовательность последо- вательности Sn .

Из теории пределов последовательностей известны следующие утверждения.

1. Если последовательность Sn сходится, то любая ее подпосле- довательность (в том числе и S%n = SNn −1 ) сходится к тому же пределу.

∞	∞
Значит, сходимость ряда åak влечет сходимость ряда	åAk ,
k=1	k=1
причем суммы обоих рядов равны.

2. Сходимость подпоследовательности S%n = SNn −1 , вообще говоря, не влечет сходимости последовательности Sn , поэтому из сходимо-

∞	∞
сти ряда åAk	в общем случае не следует сходимость ряда åak .
k=1	k=1

На основании этих утверждений можно сформулировать следу- ющую теорему.

Теорема 1.19. В сходящемся ряде допустима произвольная расстановка скобок. Полученный ряд будет сходиться к сумме исходного ряда.

1.3.2. Ряды лейбницевского типа

∞

Ряд å(−1)k +1 ak называется рядом лейбницевского типа, если:

	k=1
1)	lim ak = 0;
	k→∞
2)	"k ak ³ ak+1 ³ 0 (или "k ak £ ak+1 £ 0).

Теорема 1.20 (признак Лейбница). Ряд лейбницевского типа сходится, причем его сумма S не превышает a1 , т.е. 0 £ S £ a1

(или a1 £ S £ 0).

Рассмотрим случай "k ak ³ ak+1 ³ 0. Частичные суммы четного

порядка для данного ряда можно записать в виде

2n	= a1 − (a2 − a3 )− (a4 − a5 ) −...− a2n
å(−1)k+1 ak	= a1 − (a2 − a3 )− (a4 − a5 ) −...− a2n	(1.15)
k =1
или
2n	(a1 − a2 )+ (a3 − a4 ) + ...+ (a2n−1 − a2n ).
å(−1)k+1 ak =	(a1 − a2 )+ (a3 − a4 ) + ...+ (a2n−1 − a2n ).	(1.16)

k=1

Сучетом условия ak ³ ak+1 ³ 0 из (1.16) следует, что рассматрива-

емая последовательность частичных сумм возрастает, т.е. S2n £ S2(n+1) ,

а из (1.15) следует ее ограниченность сверху числом a1 . Значит,

данная последовательность сходится. Пусть lim S2n = S . Тогда

n→∞

lim S	2n+1	= lim(S	2n	+ a	) = lim S	2n	+ lima	2n+1	= S + 0 = S .
n→∞	2n+1	n→∞	2n	2n+1	n→∞	2n	n→∞	2n+1

Таким образом, lim Sn = S , т.е. ряд лейбницевского типа сходится.

n→∞

Следствие. Для остатка ряда лейбницевского типа справедливы неравенства

rn ≤ an+1 и rnan+1 ³ 0,

т.е. остаток ряда не превосходит по абсолютной величине значения первого отбрасываемого слагаемого и совпадает с ним по знаку.

Остаток ряда лейбницевского типа также является рядом лейб- ницевского типа, поэтому, если an+1 > 0 , то выполняется неравенство

0 £ rn £ an+1 , а если an+1 < 0, то an+1 £ rn £ 0 .

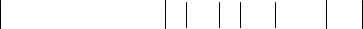
1.3.3. Абсолютная и условная сходимость

	∞
Ряд åak называется абсолютно сходящимся,						если сходится
	k=1			∞
∞			∞	∞
ряд å	ak		. Если ряд åak сходится, а ряд	å	ak	расходится, то
ряд å	ak		. Если ряд åak сходится, а ряд	å	ak	расходится, то
k=1			k=1	k=1
∞
ряд åak		называется условно сходящимся.

k=1

За м е ч а н и е 1 . Из определения видно, что если знакопостоян-

ный ряд сходится, то он сходится абсолютно, поэтому понятия «абсолютно сходящийся ряд» и «условно сходящийся ряд» имеют смысл только для знакочередующихся рядов.

За м е ч а н и е 2 . Согласно определению, если знакопеременный ряд сходится, то он сходится либо абсолютно, либо условно.

За м е ч а н и е 3 . Для исследования абсолютной сходимости ряда могут быть применены все признаки сходимости рядов с неотрица- тельными членами.

Теорема 1.21. Абсолютно сходящийся ряд сходится.

Утверждение теоремы следует из критерия Коши и неравенства an+1 + an+2 +...+ an+ p ≤ an+1 + an+2 +...+ an+ p .

∞
Ряд åak	называется безусловно сходящимся, если для любой
k=1	ϕ(k ) натурального ряда (ϕ есть биекция ¥ на ¥)
перестановки	ϕ(k ) натурального ряда (ϕ есть биекция ¥ на ¥)

∞

ряд åaϕ(k ) сходится. В дальнейшем будет показано, что понятия

k=1

абсолютной и безусловной сходимости ряда эквивалентны.

∞

Теорема 1.22. Если ряд åak сходится абсолютно, то он сходится

k=1

безусловно, причем его сумма при перестановке членов не меняется. * Пусть ряд

∞
åak	(1.17)
k=1
сходится абсолютно и сумма этого ряда равна S , а ряд
∞
åaϕ(k )	(1.18)

k=1

получен из ряда (1.17) с помощью перестановки ϕ. Докажем, что

"e > 0 $N "n ³ N åaϕ(k ) - S < e.

k =1

Исходя из абсолютной сходимости ряда (1.17)

"e > 0

$N0 "p å ak < e

N0 + p

k=N0 +1

åak - S

< e .

k=1

Выберем N так, чтобы k ≤ N0

ϕ(k ) ≤ N . Тогда

åaϕ(k ) - S

åaϕ(k ) - åak

åak - S

k=1

(1.19)

(1.20)

(1.21)

Покажем, что при

	n	N0		ε
"n ³ N	åaϕ(k ) - åak		<		.

	k=1	k=1	2
		n	N0
Для этого рассмотрим разность		åaϕ(k ) − åak , представляющую
		k=1	k=1

собой сумму (n − N0 ) членов ряда (1.17) с номерами, большими N0 .

Выбирая p так, чтобы номер N0 + p превосходил все эти номера,

получаем

n	N0		N0 + p			ε
åaϕ(k ) - åak		£	å	ak	<		.	(1.22)

						2
k=1	k=1		k=N0 +1

Из неравенств (1.20) – (1.22) получаем åaϕ(k ) - S < e , а значит,

k =1

ряд (1.18) сходится и имеет сумму, равную S .

З а м е ч а н и е . Эта теорема часто используется в одной из следу- ющих формулировок: «при любой перестановке абсолютно сходя- щегося ряда сумма полученного ряда равна сумме исходного» или «сумма абсолютно сходящегося ряда не зависит от порядка его чле- нов». Последняя формулировка удобна, если речь идет о сумме некоторого счетного множества чисел, нумерация которого еще не установлена или устанавливается произвольно.

Теорема 1.23 (теорема Коши об абсолютно сходящемся ряде).

Если ряд сходится абсолютно, то любой ряд, полученный из данно- го ряда посредством некоторой перестановки членов, также сходит- ся абсолютно и имеет ту же сумму, что и данный ряд.

* Данная теорема является следствием предыдущей. Для дока-

∞

зательства абсолютной сходимости ряда åaϕ(k ) , полученного пере-

k=1

становкой членов исходного ряда, достаточно применить теорему

∞		∞
1.22 к рядам å	ak	и å	aϕ(k )	.

k=1		k =1

Теорема 1.24 (теорема Римана об условно сходящемся ряде).

Если ряд сходится условно, то, каково бы ни было наперед взятое число L (конечное или бесконечное), можно так переставить члены этого ряда, чтобы преобразованный ряд сходился к числу L .

* Пусть ряд

∞
åak	(1.23)

k=1

сходится условно. В этом случае можно утверждать, что он содержит бесконечное число как положительных, так и отрицательных членов (иначе, отбрасывая конечное число членов ряда, мы бы получили зна- копостоянный ряд, который сходится абсолютно). Пусть p1, p2 , p3 ,... –

положительные, а q1,q2 ,q3 ,... – отрицательные члены ряда (1.23), выписанные в таком порядке, в каком они стоят в этом ряду.

∞	∞
Введем в рассмотрение два знакопостоянных ряда: å pk	и åqk .
k=1	k=1

Пусть Pn и Qn – соответствующие суммы всех положительных и от- рицательных членов ряда (1.23), составляющие его частичную сумму

Sn . Очевидно, что Sn = Pn + Qn . Так как ряд (1.23) сходится условно,

	lim(Pn + Qn ) = S ,		(1.24)
	n→∞
	lim(Pn − Qn ) = ∞.		(1.25)
	n→∞	lim Pn	= ∞ , limQn = ∞ ,
Сопоставляя (1.24) и (1.25), получим, что		lim Pn	= ∞ , limQn = ∞ ,
∞	∞	n→∞	n→∞
∞	∞
т.е. ряды å pk	и åqk расходятся, следовательно,
k=1	k=1
	N +m1	N +m2
E > 0 N m1 å pk > E и m2		å qk	< −E .
	k=N +1	k=N +1

Пусть L < ∞ . Переставим члены ряда (1.23) таким образом,

чтобы lim Sn = L . Для этого сначала выберем из ряда ровно столько

n→∞

положительных членов p1,..., pn1 , чтобы их сумма å pk превзошла L .

k=1

Затем добавим ровно столько отрицательных членов q1,...,qn2 , чтобы

	n1	n2
общая сумма å pk		+ åqk стала меньше L . После этого снова доба-
	k=1	k=1
вим	положительные члены pn1+1,..., pn3 так, чтобы сумма
n3	n2
å pk	+ åqk оказалась больше L . Продолжая аналогичные рассуж-
k=1	k=1

дения, мы получим ряд, в состав которого войдут все члены исход- ного ряда (1.23).

Докажем, что полученный ряд сходится к L . Для этого достаточно заметить, что величина Sn − L не превосходит модуля последнего

члена последней полностью завершенной группы членов полученного

ряда одного знака, а исходя из сходимости ряда (1.23) lim ak = 0.

k→∞

Таким образом, lim Sn − L = 0 , что и требовалось доказать.

n→∞

Если L = +∞ , то, взяв последовательность возрастающих до бес- конечности чисел {Ln} , перегруппируем члены ряда так, что после

каждой группы положительных чисел следует ровно одно отрица- тельное число, причем k -я группа положительных чисел заканчива- ется, когда частичная сумма ряда превысит Lk . При этом получится

ряд, сумма которого равна +∞ . Аналогично можно получить и ряд с суммой −∞ .

Таким образом, из теоремы Римана следует, что если ряд сходится условно, то он сходится «небезусловно» (случай беско- нечного L ). Далее, если ряд сходится неабсолютно, то он сходится условно (согласно определению). Следовательно, из неабсолютной сходимости ряда вытекает его «небезусловная» сходимость. Теоре- ма Коши при этом утверждает, что из абсолютной сходимости ряда следует его безусловная сходимость. В результате можно считать

доказанной эквивалентность понятий абсолютной и безусловной сходимости.

На практике при исследовании сходимости обычно вместо тер- мина «неабсолютная» используют термин «условная», а вместо термина «безусловная» – термин «абсолютная».

З а м е ч а н и е . Теоремы Римана и Коши подчеркивают тот факт, что неабсолютная (условная) сходимость осуществляется лишь бла- годаря взаимному погашению положительных и отрицательных чле- нов и потому существенно зависит от порядка, в котором они следу- ют один за другим, между тем как абсолютная сходимость основана на быстроте убывания этих членов и от порядка их не зависит.

П р и м е р 1.14. Найдем множества абсолютной и условной схо-

димости ряда (множества значений α , при которых ряд сходится абсолютно и условно)

∞		k−1
∞	(−1α) .
å	(−1α) .		(1.26)
k=1	k

При α ≤ 0 ряд (1.26) расходится, так как не выполняется необ- ходимое условие сходимости. В силу признака Лейбница, при α > 0 данный ряд сходится, причем при 0 < α ≤1 – условно, а при α >1 абсолютно, так как обобщенный гармонический ряд сходится при α >1 и расходится при α ≤1.

Преобразование Абеля для конечных сумм*

Пусть задана сумма S = a1b1 + a2b2 + ...+ anbn . Положим

B1 = b1 , B2 = b1 + b2 , …, Bn = b1 + b2 + ...+ bn ,

тогда

b1 = B1 , b2 = B2 − B1 , …, bn = Bn − Bn−1 ,

S = a1B1 + a2 (B2 − B1 ) +...+ an (Bn − Bn−1 ).

Раскрывая скобки и группируя по-новому члены, получим

равенство

S = (a1 − a2 )B1 + (a2 − a3 )B2 +...+ (an−1 − an )Bn−1 + an Bn .

Таким образом,

n	n−1
åak bk = å(ak − ak +1 )Bk + an Bn .		(1.27)
k=1	k=1

Такое преобразование конечных сумм называется преобразованием Абеля.

Неравенство Абеля*

Если

ak ³ ak+1 > 0 (ak £ ak+1 < 0), k =

(1.28)

1, n -1

b1 + ... + bk

£ B, k =

(1.29)

1,n

то

åak bk

£ B

(1.30)

k=1

все разности ak − ak+1

Согласно условиям

(1.28),

– одного

знака, поэтому из (1.29) и (1.27) получим

n−1

åak bk

ak - ak+1

k=1

k =1

æ n−1

ak - ak+1

£ Bç å

÷ = B

è k=1

Признаки сходимости знакопеременных числовых рядов

Теорема 1.25 (признак Дирихле). Если последовательность {ak } монотонно сходится к нулю, а последовательность частичных сумм

∞

Bn = åbk

ограничена, то ряд

åak bk сходится.

k=1

* В силу ограниченности последовательности {Bn}

B ¡+ "n

åbk

£ B ,

значит:

k=1

n+ p

n >1 p ¥

åbk

Bn+ p - Bn−1

Bn+ p

Bn−1

£ 2B . (1.31)

k=n

= 0, найдется

Пусть

задано ε > 0. Так

как по условию

lim ak

k→∞

номер n(e) такой, что "n ³ n(e) выполняется неравенство

(1.32)

n+ p

Применив неравенство Абеля (1.30) к сумме åak bk , с учетом

(1.31) и (1.32) получим

k=n

n+ p

"n ³ n(e) p ¥

åak bk

£ 2B

< e .

k=n

∞

Отсюда, согласно критерию Коши, следует, что ряд åak bk сходится.

k=1

Теорема 1.26 (признак Абеля). Если последовательность {an}

∞

монотонна и ограничена, а ряд åbk сходится, то сходится и ряд åak bk .

k=1

* В силу ограниченности последовательности {an}

A ¡+ "n

£ A.

∞

Пусть задано ε > 0. Из сходимости ряда åbk

вытекает, что

k=1

$n(e) "n ³ n(e) "p Î¥ åbk < e .

n+ p

k =n

Следовательно,	"n ³ n(e)		"p Î¥ согласно					неравенству Абеля
(1.30) справедливо неравенство
		åak bk < e an £ e ,
		n+ p

		k=n				A	∞
		k=n				A

а значит, согласно критерию Коши, ряд åak bk								сходится.
							k=1
З а м е ч а н и е .	На практике в качестве последовательности {bk }
чаще всего берется или последовательность								{(-1)ϕ(k )}, или одна
из последовательностей		{cos(ka)} и {sin (ka)}. Ограниченность
	n					при данной функции j(k ) уста-
последовательности íìå(-1)ϕ(k ) ýü						при данной функции j(k ) уста-
	î k=1			þ
навливается непосредственно. Покажем ограниченность последова-
ì	n	ü	%			ì n		ü
тельностей Bn = íåcos(ka)ý			и Bn		= íåsin(ka)ý при a¹2pk, kÎ¢.
îk =1		þ				îk =1		þ

4 k7 + 3k

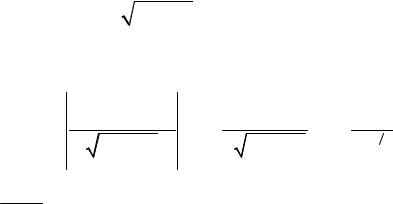
Так как

sin

× Bn =

1 æ

- sin

a ö

- sin

+...+

çsin

2 è

2 ø

(

2n +1 a

- sin

(

2n -1 a ö

çsin

)

(

2n +1 a

(

n +1 a

çsin

)

- sin

= cos

)

sin

получаем, что

cos (n +1)α sin

"a ¹ 2pk, k Î¢

≤

sin

Точно так же получаем, что

(

)

nα

sin

"a ¹ 2pk, k Î¢

≤

sin

П р и м е р 1.15. Исследуем на абсолютную и условную сходимость

ряды

∞	arctg	(	(−k )k	)	∞	(-1)	k(k+1)/ 2
1) å					; 2) å		2/3 .
						k
	4 k7 + 3k
k=1					k=1

1. Данный ряд сходится абсолютно по признаку Вейер- штрасса, так как

∞

а ряд å

k=1

2k74

∞ arctg((-k )k )

k =1

сходится.

£ å	p	£ å p7 4 ,
∞		∞

k=1 24 k7 + 3k k=1 2k

2. Данный ряд не сходится абсолютно, так как

k(k+1)/ 2

= å 12/3 ,

(-1)2/3

∞

k=1

∞

а ряд å

расходится. При этом он сходится по признаку Дирих-

2/ 3

k=1

ле, так как последовательность

монотонно сходится к 0

k2 3

k(k+1)/ 2

∞

при k → ∞,

å(-1)k(k+1)/ 2

£ 2.

Таким образом,

ряд å(-1)

2/3

k=1

сходится условно

П р и м е р

1.16. Исследуем на сходимость и абсолютную сходи-

мость ряд ∞

ln çæ1+

(-1)k

÷ö .

k=1

(

)

= t + O

(

)

при

Используя асимптотическую формулу ln 1+ t

t → 0, получим a

(-1)k

+ b , где

, C > 0.

23 k2

k4/ 3

∞

(-1)

Ряд åbk

сходится абсолютно. Ряд å

сходится согласно

23 k2

k=1

k =1

∞

признаку Лейбница, причем условно,

так как å

расходится.

∞

k=1

23 k2

Значит, ряд åak

сходится условно.

k=1

Пр и м е р 1.17. Найдем множества абсолютной и условной сходи- мости рядов:

1) åsin (bk )		;	2) åsin (b/ k ) .
∞			∞
k=1	k		k=1	k

1. При β = πm, m ¢ все члены ряда равны нулю и ряд сходит-

ся абсолютно.

Исследуем данный ряд на абсолютную сходимость при осталь- ных значениях β .

Так как

sin (bk )

³ sin2 (bk ), то

å sin

(bk )

³ åsin

(bk )

= å1- cos(

2bk ) .

∞

k=1

∞

(2bk )

Ряд å

cos

сходится по признаку Дирихле, так как после-

k=1

довательность íìåcos(2bk )ýü ограничена по модулю числом

sinb

î k=1

1 ü

а последовательность í

ý монотонно сходится к 0 при n → ∞ . Ряд

∞

î2nþ

расходится. Так как ряд,

являющийся суммой сходящегося и

k =1

расходящегося рядов, расходится, исследуемый ряд не сходится

абсолютно при b ¹ pm, mÎ¢.

∞

По признаку Дирихле можно доказать,

что ряд å

sin (bk )

схо-

∞

k=1

sin (bk )

дится при b ¹ 2pm, mÎ¢. Таким образом, ряд å

сходится

абсолютно при b = pm,

mÎ¢,

k=1

а при остальных значениях b схо-

дится условно.

∞

Ряд å

sin(b k )

сходится

абсолютно

"bÎ¡,

так

как

sin (b k )

k=1

: b2

при k → ∞, а ряд å b2 сходится "bÎ¡.

∞

k=1

З а м е ч а н и е . Множества абсолютной и условной сходимости

∞

ряда åak (b) не пересекаются, а их объединение образует все мно-

k=1

∞

жество сходимости ряда åak (b). Таким образом, все множество

k=1

допустимых значений α разбивается на три непересекающихся множества (некоторые могут быть пустыми): множество расходи- мости ряда, множество условной сходимости ряда и множество абсолютной сходимости ряда.

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.08.20191.19 Mб5Электроника_лекции.doc
#
03.11.2018216.34 Кб5электронный вариант.docx
#
06.05.20191.92 Mб26Электронный курс по MathCAD.doc
#
25.09.2019332.74 Кб10Электростатика.docx
#
27.03.2015444.93 Кб86Элементы солнечной батареи.doc
#
11.03.2016951.2 Кб26Элементы теории рядов.pdf
#
25.08.20199.21 Mб58ЭМ и ЭМ ПП в ЭЭС задачник.doc
#
01.09.20192.88 Mб14ЭМ и ЭМ ПП в ЭЭС. Все, что надо знать..doc
#
13.08.201989.09 Кб2Эмиль Дюркгейм на семинар.doc
#
27.03.20151.58 Mб14ЭнБ-91_1 .docx
#
27.03.2015570.73 Кб9ЭнБ-91_2 .docx