
- •3.3. Выборочные начальные и центральные моменты. Асимметрия. Эксцесс
- •3.4. Упрощенный способ вычисления выборочных характеристик распределения
- •3.5. Графическое изображение вариационных рядов
- •3.6. Статистические оценки параметров распределения
- •3.7. Интервальное оценивание
- •3.8. Оценки истинного значения измеряемой величины и точности измерений
- •3.9. Статистическая проверка гипотез
- •3.10. Сравнение двух дисперсий нормальных генеральных совокупностей
- •3.11. Сравнение двух средних нормальных генеральных совокупностей
3.6. Статистические оценки параметров распределения
Пусть
x1,
x2,
…, xn
– выборка объема n
из генеральной совокупности с функцией
распределения F(x
). Рассмотрим методы нахождения оценок
параметров этого распределения.
Рассмотрим для этого выборочное
распределение, т.е. распределение
дискретной случайной величины, принимающей
значения x1,
x2,
…, xn
с вероятностями, равными 1/n
. Числовые характеристики этого
выборочного распределения называются
выборочными
(эмпирическими)
числовыми
характеристиками.
Следует отметить, что выборочные числовые
характеристики являются характеристиками
данной выборки, но не являются
характеристиками распределения
генеральной совокупности. Однако эти
характеристики можно использовать для
оценок параметров генеральной
совокупности.
Точечной
называют статистическую оценку, которая
определяется одним числом.
Несмещенной
называют точечную оценку, математическое
ожидание которой равно оцениваемому
параметру при любом объеме выборки.
Точечная оценка называется состоятельной,
если при неограниченном увеличении
объема выборки (n
=> ∞) она сходится по вероятности к
истинному значению параметра.
Эффективной
называют точечную оценку, которая (при
заданном объеме выборки n)
имеет наименьшую возможную дисперсию.
В математической статистике показывается,
что состоятельной, несмещенной оценкой
генерального среднего значения а
является выборочное среднее
арифметическое:
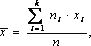 гдехi
– варианта выборки, ni
– частота варианты хi,
–
гдехi
– варианта выборки, ni
– частота варианты хi,
–
![]() объем
выборки.
Для упрощения
расчета целесообразно перейти к условным
вариантам
объем
выборки.
Для упрощения
расчета целесообразно перейти к условным
вариантам![]() (в
качествес
выгодно брать первоначальную варианту,
расположенную в середине вариационного
ряда). Тогда
(в
качествес
выгодно брать первоначальную варианту,
расположенную в середине вариационного
ряда). Тогда
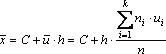 .
Эффективность или неэффективность
оценки зависит от вида закона распределения
случайной величиныХ.
Если величина Х
распределена по нормальному закону, то
оценка
.
Эффективность или неэффективность
оценки зависит от вида закона распределения
случайной величиныХ.
Если величина Х
распределена по нормальному закону, то
оценка
![]() является
эффективной. Для других законов
распределения это может быть и не
так.Несмещенной
оценкой генеральной дисперсии
служит исправления выборочная
дисперсия
является
эффективной. Для других законов
распределения это может быть и не
так.Несмещенной
оценкой генеральной дисперсии
служит исправления выборочная
дисперсия
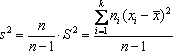 ,
так как
,
так как![]() ,
где σ2
– генеральная дисперсия. Более удобна
формула
,
где σ2
– генеральная дисперсия. Более удобна
формула
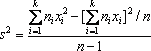 .
Если
.
Если![]() .
Оценкаs2
для генеральной дисперсии является
также и состоятельной, но не является
эффективной. Однако в случае нормального
распределения она является «асимптотически
эффективной», то есть при увеличении
n
отношение ее дисперсии к минимально
возможной неограниченно приближается
к единице.
Итак, если
дана выборка из распределения F(x)
случайной величины Х
с неизвестным математическим ожиданием
а
и дисперсией σ2
, то для вычисления значений этих
параметров мы имеем право пользоваться
следующими приближенными формулами:
.
Оценкаs2
для генеральной дисперсии является
также и состоятельной, но не является
эффективной. Однако в случае нормального
распределения она является «асимптотически
эффективной», то есть при увеличении
n
отношение ее дисперсии к минимально
возможной неограниченно приближается
к единице.
Итак, если
дана выборка из распределения F(x)
случайной величины Х
с неизвестным математическим ожиданием
а
и дисперсией σ2
, то для вычисления значений этих
параметров мы имеем право пользоваться
следующими приближенными формулами:
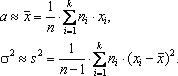
3.7. Интервальное оценивание
Выше
мы рассмотрели вопрос об оценке
неизвестного параметра а
одним числом. Такие оценки мы назвали
точечными. Они имеют тот недостаток,
что при малом объеме выборки могут
значительно отличаться от оцениваемых
параметров. Поэтому, чтобы получить
представление о близости между параметром
и его оценкой, в математической статистике
вводятся, так называемые, интервальные
оценки.
Пусть во выборке
для параметра θ найдена точечная оценка
θ*.
Обычно исследователи заранее задаются
некоторой достаточно большой вероятностью
γ (например, 0,95; 0,99 или 0,999) такой, что
событие с вероятностью γ можно считать
практически достоверным, и ставят вопрос
об отыскании такого значения ε > 0, для
которого
![]() .
Видоизменив это равенство, получим:
.
Видоизменив это равенство, получим:![]() и будем в этом случае говорить, что
интервал ]θ*–ε;
θ*+ε[
покрывает оцениваемый параметр θ с
вероятностью γ.
Интервал
]θ*–ε
θ*+ε[
называется доверительным
интервалом.
Вероятность γ называется надежностью
или
доверительной вероятностью
интервальной оценки.
Концы доверительного интервала, т.е.
точки θ*–ε
и θ*+ε
называются доверительными
границами.
Число ε называется точностью
оценки.
В качестве примера задачи об определении
доверительных границ, рассмотрим вопрос
об оценке математического ожидания
случайной величины Х,
имеющей нормальный закон распределения
с параметрами а
и σ, т.е. Х
= N(a,σ).
Математическое ожидание в этом случае
равно а.
По наблюдениям x1,
x2,
…, xn
вычислим среднее
и будем в этом случае говорить, что
интервал ]θ*–ε;
θ*+ε[
покрывает оцениваемый параметр θ с
вероятностью γ.
Интервал
]θ*–ε
θ*+ε[
называется доверительным
интервалом.
Вероятность γ называется надежностью
или
доверительной вероятностью
интервальной оценки.
Концы доверительного интервала, т.е.
точки θ*–ε
и θ*+ε
называются доверительными
границами.
Число ε называется точностью
оценки.
В качестве примера задачи об определении
доверительных границ, рассмотрим вопрос
об оценке математического ожидания
случайной величины Х,
имеющей нормальный закон распределения
с параметрами а
и σ, т.е. Х
= N(a,σ).
Математическое ожидание в этом случае
равно а.
По наблюдениям x1,
x2,
…, xn
вычислим среднее
![]() и
оценку
и
оценку![]() дисперсии
σ2.
Оказывается, что по данным выборки можно
построить случайную величину
дисперсии
σ2.
Оказывается, что по данным выборки можно
построить случайную величину
![]() ,
которая имеет распределение Стьюдента
(илиt-распределение)
с ν=n–1
степенями свободы.
Воспользуемся таблицей П.3 и найдем для
заданных вероятности γ и числа n
число tγ
такое, при котором вероятность
P(|Т|
< tγ)
= γ, или
,
которая имеет распределение Стьюдента
(илиt-распределение)
с ν=n–1
степенями свободы.
Воспользуемся таблицей П.3 и найдем для
заданных вероятности γ и числа n
число tγ
такое, при котором вероятность
P(|Т|
< tγ)
= γ, или
 .
Сделав очевидные преобразования,
получим
.
Сделав очевидные преобразования,
получим![]() Итак, пользуясь распределением Стьюдента,
мы нашли доверительный интервал
Итак, пользуясь распределением Стьюдента,
мы нашли доверительный интервал![]() ,
покрывающий неизвестный параметра
с надежностью γ. Здесь случайные величины
,
покрывающий неизвестный параметра
с надежностью γ. Здесь случайные величины
![]() иS
заменены неслучайными величинами
иS
заменены неслучайными величинами
![]() иs,
найденными по выборке. По таблице П.3,
по заданным n
и γ можно найти tγ
.
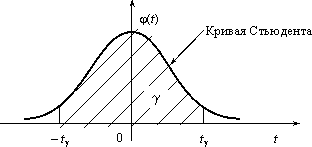
Графическая иллюстрация
схемы нахождения точности ε и доверительных
границ, отвечающих надежности γ приведена
на рис. 5.1. Доверительная вероятность γ
будет соответствовать площади под
кривой Стьюдента, заключенной между
точками –tγ
и tγ.
иs,
найденными по выборке. По таблице П.3,
по заданным n
и γ можно найти tγ
.
Графическая иллюстрация
схемы нахождения точности ε и доверительных
границ, отвечающих надежности γ приведена
на рис. 5.1. Доверительная вероятность γ
будет соответствовать площади под
кривой Стьюдента, заключенной между
точками –tγ
и tγ.
![]()
![]()
![]()
![]() Рис. 3
.1
Замечание. Приn
=> ∞ распределение Стьюдента стремится
к нормальному распределению. Поэтому
при больших n
(практически при n
≥ 30) tγ
можно получить по таблице П.2 из уравнения
Ф(tγ)
= γ/2.
Для оценки среднего
квадратического отклонения s нормально
распределенного количественного
признака Х
с надежностью g по исправленному
выборочному среднему квадратическому
отклонению s
служат доверительные интервалы:
s(1
– q) < s < s
(1 + q)
при q<1,
0 < s < s(1
+ q)
при q>1,
где q находят по таблице П. 4 по заданным
n
и γ.
Задача
3.1.
Найти доверительные интервалы для
оценки математического ожидания а
и среднего квадратического отклонения
s выручки магазина по результатам
вычислений из 3.4. Надежность γ = 0,95.
Решение.
Ниже будет показано, что распределение
выручки магазина является нормальным.
В 4.4 были получены следующие точечные
оценки а≈
Рис. 3
.1
Замечание. Приn
=> ∞ распределение Стьюдента стремится
к нормальному распределению. Поэтому
при больших n
(практически при n
≥ 30) tγ
можно получить по таблице П.2 из уравнения
Ф(tγ)
= γ/2.
Для оценки среднего
квадратического отклонения s нормально
распределенного количественного
признака Х
с надежностью g по исправленному
выборочному среднему квадратическому
отклонению s
служат доверительные интервалы:
s(1
– q) < s < s
(1 + q)
при q<1,
0 < s < s(1
+ q)
при q>1,
где q находят по таблице П. 4 по заданным
n
и γ.
Задача
3.1.
Найти доверительные интервалы для
оценки математического ожидания а
и среднего квадратического отклонения
s выручки магазина по результатам
вычислений из 3.4. Надежность γ = 0,95.
Решение.
Ниже будет показано, что распределение
выручки магазина является нормальным.
В 4.4 были получены следующие точечные
оценки а≈
![]() =
30,77 тыс. руб.,
=
30,77 тыс. руб.,![]() (тыс.
руб)2,
где n=90
– объем выборки. Следовательно, σ≈s=6,83
тыс.руб.
По таблице П.1.2
при γ/2 =0,475 находим tγ=
1,96. Вычисляем точность оценки
(тыс.
руб)2,
где n=90
– объем выборки. Следовательно, σ≈s=6,83
тыс.руб.
По таблице П.1.2
при γ/2 =0,475 находим tγ=
1,96. Вычисляем точность оценки
![]() ,
доверительные границы
,
доверительные границы![]() .
Получаем доверительный интервал 29,4<a
< 32,2.
Находим доверительный
интервал для оценки σ. По таблице П.4 при
γ = 0,95 и n
= 90 получаем q
= 0,151. Вычисляем доверительные границы
s
(1 – q)=6,83∙0,849
≈ 5,8 и s
(1+q)
= 6,83∙1,151 ≈ 7,9. Получаем доверительный
интервал 5,8 < σ < 7,9.
.
Получаем доверительный интервал 29,4<a
< 32,2.
Находим доверительный
интервал для оценки σ. По таблице П.4 при
γ = 0,95 и n
= 90 получаем q
= 0,151. Вычисляем доверительные границы
s
(1 – q)=6,83∙0,849
≈ 5,8 и s
(1+q)
= 6,83∙1,151 ≈ 7,9. Получаем доверительный
интервал 5,8 < σ < 7,9.
