Если исходная информация представлена в виде интервального ряда распределения, то средняя арифметическая взвешенная определяется по формуле:

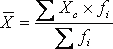
где X_c - центральное (серединное) значение признака в интервале.

Например: По имеющимся данным определить средний стаж рабочего бригады:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
Численность рабочих, чел. (fi)	3	4	7	10	6

Для расчёта средней арифметической взвешенной интервального ряда распределения определим центральное (серединное) значение признака в каждом интервале. Среднее значение интервала находится как полусумма нижней границы данного интервала и нижней границы следующего интервала:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
(Xc )

Оформим исходные данные а следующем виде:

Стаж работы, лет	0 - 2	2 - 4	4 - 6	6 - 8	8 - 10
(Xc )	1	3	5	7	9
Численность рабочих, чел. (fi)	3	4	7	10	6

 

Средний стаж рабочего бригады составляет

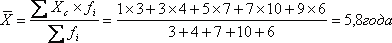
Расчет моды и медианы в интервальном ряду

В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул: 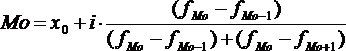, (5.6) гдеx₀ – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); i – величина модального интервала; f_Mo – частота модального интервала; f_Mo-1 – частота интервала, предшествующего модальному; f_Mo+1 – частота интервала, следующего за модальным. 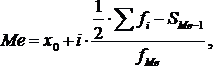(5.7) гдеx₀ – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); i – величина медианного интервала; S_Me-1 – накопленная интервала, предшествующего медианному; f_Me – частота медианного интервала. Проиллюстрируем применение этих формул, используя данные табл. 5.10. Интервал с границами 60 – 80 в данном распределении будет модальным, т.к. он имеет наибольшую частоту. Использую формулу (5.6), определим моду: Для установления медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит половины суммы накопленных частот (в нашем случае 50 %) (табл. 5.11). Установили, что медианным является интервал с границами 100 – 120 тыс. руб. Определим теперь медиану: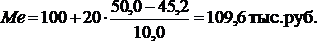Таблица 5.10 - Распределение населения РФ по уровню среднедушевых номинальных денежных доходов в марте 1994г.

Группы по уровню среднедушевого месячного дохода, тыс. руб.	Удельный вес населения, %
До 20	1,4
20 – 40	7,5
40 – 60	11,9
60 – 80	12,7
80 – 100	11,7
100 – 120	10,0
120 – 140	8,3
140 –160	6,8
160 – 180	5,5
180 – 200	4,4
200 – 220	3,5
220 – 240	2,9
240 – 260	2,3
260 – 280	1,9
280 – 300	1,5
Свыше 300	7,7
Итого	100,0

Таблица 5.11 - Определение медианного интервала

Интервал, тыс. руб.	Накопленная частота, %
До 20	1,4
20 – 40	8,9
40 – 60	20,8
60 – 80	33,5
80 – 100	45,2
100 – 120	55,2

Таким образом, в качестве обобщенной характеристики значений определенного признака у единиц ранжированной совокупности могут быть использованы средняя арифметическая, мода и медиана. Основной характеристикой центра распределения является средняя арифметическая, для которой характерно то, что все отклонения от нее (положительные и отрицательные) в сумме равняются нулю. Для медианы характерно, что сумма отклонений от нее по модулю является минимальной, а мода представляет собой значение признака, которое наиболее часто встречается. Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. В симметричных распределениях все три характеристики совпадают. Чем больше расхождение между модой и средней арифметической, тем более асимметричен ряд. Для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней, т.е.: |Mo –`x| = 3 |Me –`x|.

Определение моды и медианы графическим методом

Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Из точки их пересечения опускаем перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения (рис. 5.3). 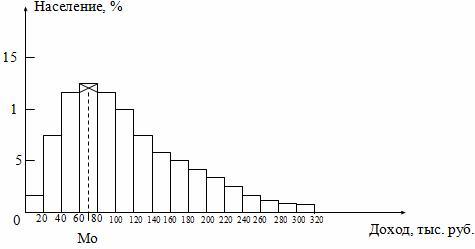Рис. 5.3. Графическое определение моды по гистограмме.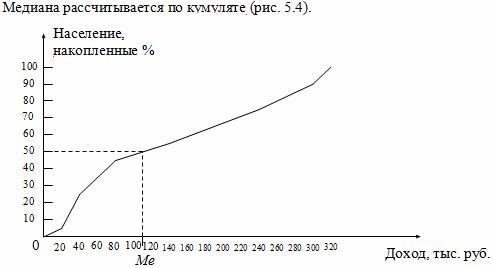Рис. 5.4. Графическое определение медианы по кумуляте Для определения медианы из точки на шкале накопленных частот (частостей), соответствующей 50 %, проводится прямая, параллельная оси абсцисс до пересечения с кумулятой. Затем из точки пересечения опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.

3.3. Выборочные начальные и центральные моменты. Асимметрия. Эксцесс

     Приведем краткий обзор характеристик, которые применяются для анализа вариационного ряда и являются аналогами соответствующих числовых характеристик случайной величины.      Начальным выборочным моментом k-го порядка называется величина, определяемая по формуле:      ,      гдех_i – наблюдаемое значение с частотой n_i, n – число наблюдений. В частности, начальный выборочный момент первого порядка обозначается и называетсявыборочной средней:      .Медианой называется значение признака, приходящееся на середину ранжированного ряда наблюдений.      Модой называется вариант, которому соответствует наибольшая частота.      Вариационный размах R равен разности между наибольшим и наименьшим вариантом ряда.      Центральным выборочным моментом k-го порядка называется величина, определяемая по формуле:      .      В частности, центральной выборочный момент второго порядка обозначаетсяS² и называется выборочной дисперсией:      .      Средним квадратическим отклонением S называется арифметическое значение корня квадратного из дисперсии: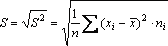.      Коэффициентом вариации называется отношение среднего квадратического отклонения к средней, выраженное в процентах:.      Справедливы следующие формулы, выражающие центральные выборочные моменты различных порядков через начальные:и т.д.      Выборочным коэффициентом асимметрии называется число, определяемое формулой.      Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона (см. далее) вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.      В случае отрицательного коэффициента асимметрии более пологий «спуск» полигона наблюдается слева, в противном случае – справа. В первом случае асимметрию называют левосторонней, а во втором – правосторонней.      Выборочным эксцессом или коэффициентом крутизны называется числоE^˜k, определяемое формулой      .      Выборочный эксцесс служит для сравнения на «крутость» выборочного распределения с нормальным распределением. Ранее подчеркивалось, что эксцесс для случайной величины, распределенной нормально, равен нулю. Поэтому за стандартное значение выборочного эксцесса принимаютE^˜k = 0. Если выборочному распределению соответствует отрицательный эксцесс, то соответствующий полигон имеет более пологую вершину по сравнению с нормальной кривой. В случае положительного эксцесса полигон более крутой по сравнению с нормальной кривой.

3.4. Упрощенный способ вычисления выборочных характеристик распределения

     Для вычисления выборочных характеристик (выборочной средней, дисперсии, асимметрии и эксцесса) целесообразно пользоваться вспомогательной таблицей 3.5, которая составляется так:      1) используя данные таблицы 3.3, найдем середину каждого интервала и заполним столбец 1 табл. 3.5;      2) во второй столбец записывают частотыn_i, складывают все частоты и их сумму (объем выборки n) помещают в нижнюю клетку столбца;      3) в третий столбец записывают условные варианты , причем в качестве ложного нуля С выбирают варианту, которая имеет наибольшую частоту или занимает среднее положение в ряду данных, и полагают h равным разности между любыми двумя соседними вариантами (длина интервалаb_i – a_i); по данным примера С = 31,4, h = 4,5; практически же третий столбец заполняется так: в клетке третьего столбца, которая принадлежит строке, содержащей наибольшую частоту, пишем 0; над нулем последовательно –1, –2, –3, а под нулем 1, 2, 3, 4, 5. Дальнейший порядок заполнения таблицы простой и не требует пояснений. Последний столбец таблицы – контрольный. Контроль выполняется по правилу:      .      В нашем примере имеем: 1707 + 4∙101 + 6∙207 + 4∙(–13) + 90 = 3391. Следовательно, вычисления произведены правильно.      В итоге получаем расчетную таблицу 3.5.      Таблица 3.5      Вспомогательная таблица для вычисления выборочных характеристик

xi	ni	ui	ni×ui	niui2	ni×ui3	ni×ui4	ni×(ui +1)4
1	2	3	4	5	6	7	8
17,9	4	–3	–12	36	–108	324	64
22,4	11	–2	–22	44	–88	176	11
26,9	23	–1	–23	23	–23	23	0
31,4	27	0	0	0	0	0	27
35,9	13	1	13	13	13	13	208
40,4	8	2	16	32	64	128	648
44,9	2	3	6	18	54	162	512
49,4	1	4	4	16	64	256	625
53,9	1	5	5	25	125	625	1296
Σ	90		–13	207	101	1707	3391

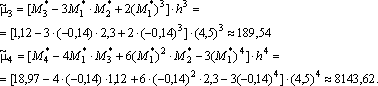     Выборочный условный момент k-го порядка определяется по формуле      По данным примера.      Вычислим искомые выборочные среднюю и дисперсию:Выборочное среднее квадратическое отклонение.      Найдем центральные эмпирические моменты третьего и четвертого порядка:Найдем значение коэффициента асимметрии и эксцесса:МедианаM^˜e – значение признака, приходящееся на середину ранжированного ряда наблюдений.      Для интервального ряда медиану следует вычислять по формуле      ,      гдеM^˜e означает номер медианного интервала, (M^˜e–1) – интервала, предшествующего медианному.      В нашем примере .      МодаM^˜o для совокупности наблюдений равна тому значению признака (табл. 3.2), которому соответствует наибольшая частота.      Для одномодального интервального ряда моду можно вычислить по формуле  ,      гдеM^˜o означает номер модального интервала (интервал с наибольшей частотой), (M^˜o–1) и (M^˜o+1) – номера предшествующего модальному и следующего за ним интервалов.      В примере .      Так как по величине,M^˜o и M^˜e мало отличаются друг от друга, есть основания предполагать теоретическое распределение нормальным.      Коэффициент вариации .      Коэффициент вариации является относительной мерой рассеяния признака.      Коэффициент вариации используется и как показатель однородности выборочных наблюдений. Считается, что если коэффициент вариации не превышает 10%, то выборку можно считать однородной, т.е. полученной из одной генеральной совокупности.      Однако к коэффициенту вариации нужно подходить с осторожностью. Продемонстрируем возможность ошибки на следующем примере. Если на основании многолетних наблюдений среднее арифметическое среднесуточных температур 8 марта составляет в какой-либо местности 0° С, то получим бесконечный коэффициент вариации независимо от разброса температур. Поэтому в данном случае коэффициент вариации не применим в качестве показателя рассеяния температур, а специфику явления более объективно оценивает стандартное отклонениеS .      Практически коэффициент вариации применяется в основном для сравнения выборок из однотипных генеральных совокупностей.