19. Механические (упругие) волны. Основные характеристики волн. Уравнение плоской волны. Поток энергии и интенсивность волны. Вектор Умова.

Любое возмущение состояния вещества или поля, распространяющиеся в пространстве с течением времени называются волнами.

Механической волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию. Различают два основных вида механических волн: упругие волны (распространение упругих деформаций) и волны на поверхности жидкости. Упругие волны возникают благодаря связям, существующим между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с конечной скоростью.

Пусть волна распространяется вдоль оси ОХ без затухания так, что амплитуды колебаний всех точек одинаковы и равны. Пусть в источнике волн изменения колеблющейся системы происходят по закону:

До точки с некоторой произвольной координатой х возмуще­ние от начала координат дойдет через время τ(знак с формулы), поэтому колебания этой точки запаздывают

Т.к время и скорость связаны зависимостью ,

,то получаем :

Это и есть уравнение плоской волны

Основные характеристики волн:

• Частота волны – частота колебаний точек среды, в которой распространяется волна.

• Фронт волны – геометрическое место точек, до которых к данному моменту дошло колебание (возмущение среды).

• Скорость волны (v) – скорость перемещения её фронта.

• Длина волны – расстояние, на которое перемещается её фронт за время, равное периоду колебаний частиц среды.

Колеблющийся источник волн обладает энергией. В процессе распространения волны каждая частица среды, до которой доходит волна, также колеблется и имеет энергию.

Выделим некоторый объем V упругой среды, в которой распространяется волна с амплитудой A и циклической частотой ω. В этом объеме имеется средняя энергия

где m - масса выделенного объема среды.

Средняя плотность энергии волны есть энергия волны, сосредоточенная в единице объема среды:

где ρ - плотность среды.

Интенсивностью волны I называется величина, равная энергии, которую в среднем переносит волна за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волны:

где ʋ- скорость распространения волны. В векторной форме

называется вектором Умова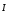

20. Внутреннее трение (вязкость жидкости). Формула Ньютона. Ньютоновские и неньютоновские жидкости. Ламинарное и турбулентное течение жидкости. Формула Гагена-Пуазейля.

В реальной жидкости вследствие взаимного притяжения и теплового движения молекул имеет место внутреннее трение, или вязкость. Ньютон установил, что сила Fтр внутреннего трения между двумя слоями жидкости, движущимися с различными скоростями зависит от природы жидкости и пропорциональная площади S соприкасающихся слоёв и градиенту скорости dv/dx между ними:

где η – коэффициент пропорциональности, называемый коэффициентом вязкости или просто вязкостью жидкости и зависящий от её природы.

Жидкость, которая подчиняется уравнению Ньютона называют ньютоновской. У большинства жидкостей (вода, низкомолекулярные органические соединения, расплавленные металлы и их соли и др.) коэффициент вязкости зависит только отприроды жидкости и температуры(с повышением температуры коэффициент вязкости понижа­ется). Такие жидкости называются ньютоновскими.а их вязкость нормальной

У некоторых жидкостей, преимущественно высокомолекулярных (например, растворы полимеров) или представляющих дисперсные системы (суспензии и эмульсии), коэффициент вязкости зависит также от режима течения — давления и градиента скорости.Такие жидкости называют неньютоновскими,а их вязкость аномальной .Например,кровь

В жидкости течение может быть ламинарным или турбулентным.

Ламинарное (слоистое) течение – течение, при котором слои жидкости текут, не перемешиваясь, скользя друг относительно друга. Распределение скоростей имеет параболический характер:

Турбулентное течение – течение, при котором скорости частиц жидкости в каждой точке беспорядочно меняются. Такое движение сопровождается появлением звука. Турбулентное течение – это хаотическое, крайне нерегулярное, неупорядоченное течение жидкости.

Скорость V_кр перехода ламинарного течения в турбулентное определяется числом Рейнольдса Re:

Количество жидкости Q, протекающее через поперечное сечение в единицу времени равно Q = vср S, где S=πR2. Следовательно

Формула Гагена-Пуазейля.

Или _______________________

–Гидравлическое сопротивление.