11. Расчет реакций в опорах валов и построение эпюр изгибающих и крутящих моментов

Величины реакций в опорах валов необходимы для проверочного расчета выбранных подшипников по динамической грузоподъёмности, а суммарные изгибающие моменты – для проверочного расчета валов на устойчивость.

Для некоторого упрощения расчета можно принять окружную силу от перекоса соединения полумуфт вала электродвигателя 1-го вала и 3-го вала и исполнительного устройства равной

F_M =0,1· F_ti =0,1∙527,5=52,75Н

приложенной к оси (на его конце) и по направлению с окружающей силой на шестерне Z ₁ или колеса Z ₄. Вылет конца вала относительно оси подшипника

l _в =3,5·d_1-1=3,5∙17=59,5=0,0595м

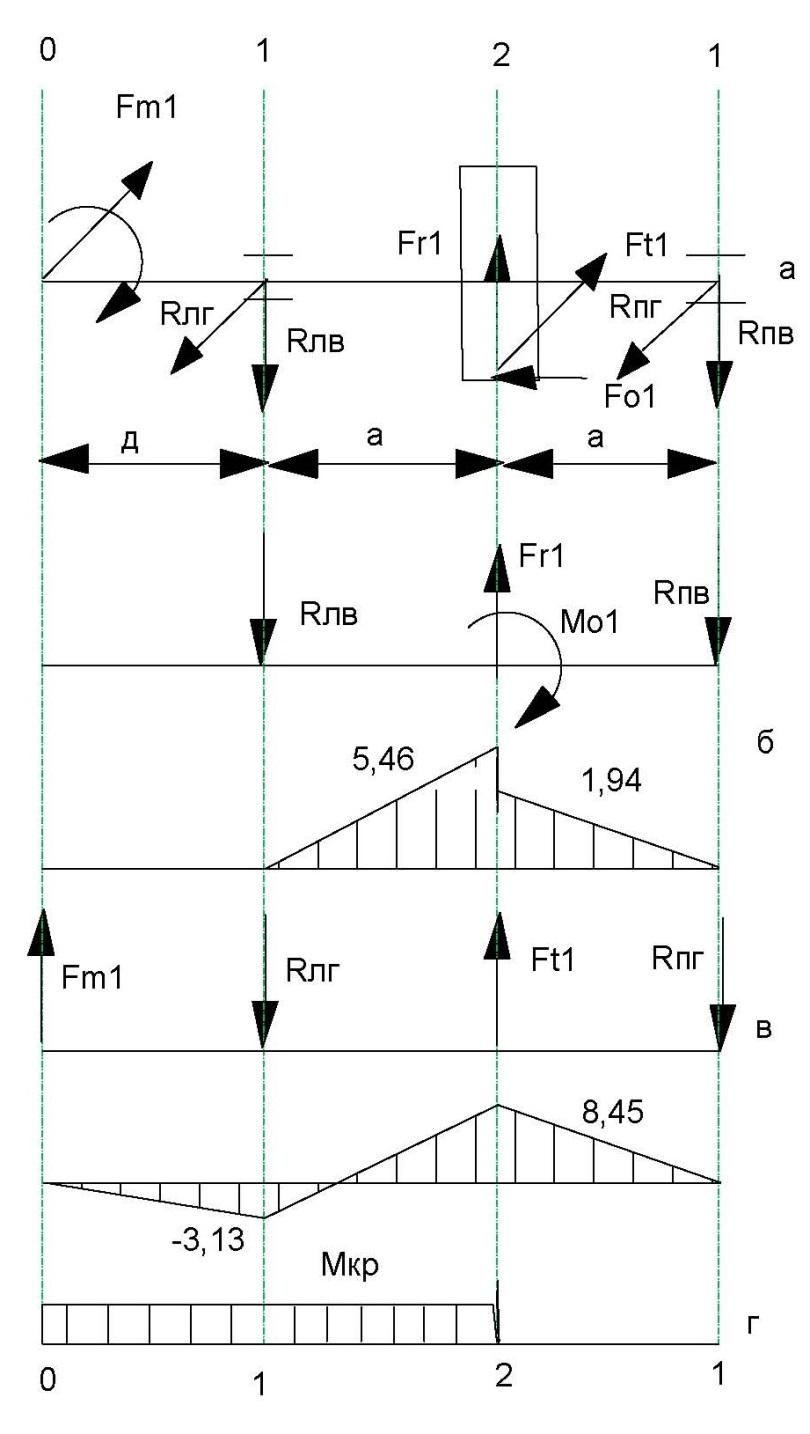
Рисунок 11.1.Расчетная схема первого вала редуктора(а),приведение сил к оси вала и эпюры изгибающих моментов в вертикальной(б) и горизонтальной(в) , крутящий момент(г).

1. Входной вал:

Силы, действующие в зацеплении:

окружная: F_t1=527,53 Н;

радиальная: F_r1=194,7 Н;

осевая: F_o1=144,5 Н;

Расчет реакций в опорах и изгибающих моментов в вертикальной плоскости:

- момент от осевой силы F_о1

M_o1= F_o1∙ d_д1/2= 144,5∙0,04868/2=3,52Н·м (11.1)

-осевая реакция

А₁=- F_o1 = -144,5Н

-сумма моментов действующих сил относительно левой опоры Л:

∑ = M_o1- F_r1∙ а + ∙2а =0 (11.2)

откуда =( F_r1∙а- M_o1)/2а=(194,7∙0,038-3,52)/0,076=51Н (11.3)

-сумма моментов действующих сил относительно правой опоры П:

∑ = M_o1+F_r1∙ а - ∙2а =0 (11.4)

Откуда =( F_r1∙а+ M_o1)/2а=(194,7∙0,038+3,52)/0,076=143,7Н

Проверка: F_r1 - - =194,7-143,7-51=0

-изгибающий момент в сечении 2(слева)

=∙а=143,7∙0,038=5,46Н·м (11.5)

-изгибающий момент в сечении 2(справа)

=∙а=51∙0,038=1,94Н·м (11.6)

Расчет реакций в опорах и изгибающих моментов в горизонтальной плоскости:

-сумма моментов действующих сил относительно левой опоры Л:

∑ = F_м1∙д –F_t1∙ а + ∙2а =0 (11.7)

Откуда =( F_t1∙ а - F_м1∙д)/2а=(527,53∙0,038-52,75∙0,0595)/0,076=222,47 Н

-сумма моментов действующих сил относительно правой опоры П:

∑ = F_t1∙ а - ∙2а +F_м1∙(д+2а) =0 (11.8)

Откуда =( F_t1∙ а + F_м1∙(д+2а))/2а=(527,53∙0,038+52,75∙0,1355)/0,076=357,81

Проверка :- -+F_t1 + F_м1=-222,47-357,81+52,75+527,53=0

-изгибающий момент в сечении 2 вала:

=∙а- F_м1 ∙(д+а)=∙а=222,47∙0,038=8,45 Н·м (11.9)

-изгибающий момент в сечении 1 вала:

=- F_м1∙д=-52,75∙0,0595=-3,13 Н·м (11.10)

Равнодействующая реакция:

- в левой опоре

∑ R_л===385,56Н (11.11)

- в правой опоре

∑ R_п===228,24Н (11.12)

-осевая в левой опоре

A= F_o1=144,5 Н.

Равнодействующий изгибающий момент:

-в сечении 1

M_и1= =- F_м1∙д=-52,75∙0,0595=-3,13 Н·м

-в сечении 2

∑ M_и2===10,06 Н·м

2. Промежуточный вал вал:

Силы, действующие в зацеплении:

окружная: F_t2=527,53 Н;

радиальная: F_r2=194,7 Н;

осевая: F_o2=144,5 Н;

окружная: F_t3=2533,8Н;

радиальная: F_r3=938,95Н;

осевая: F_o3=483,96Н;

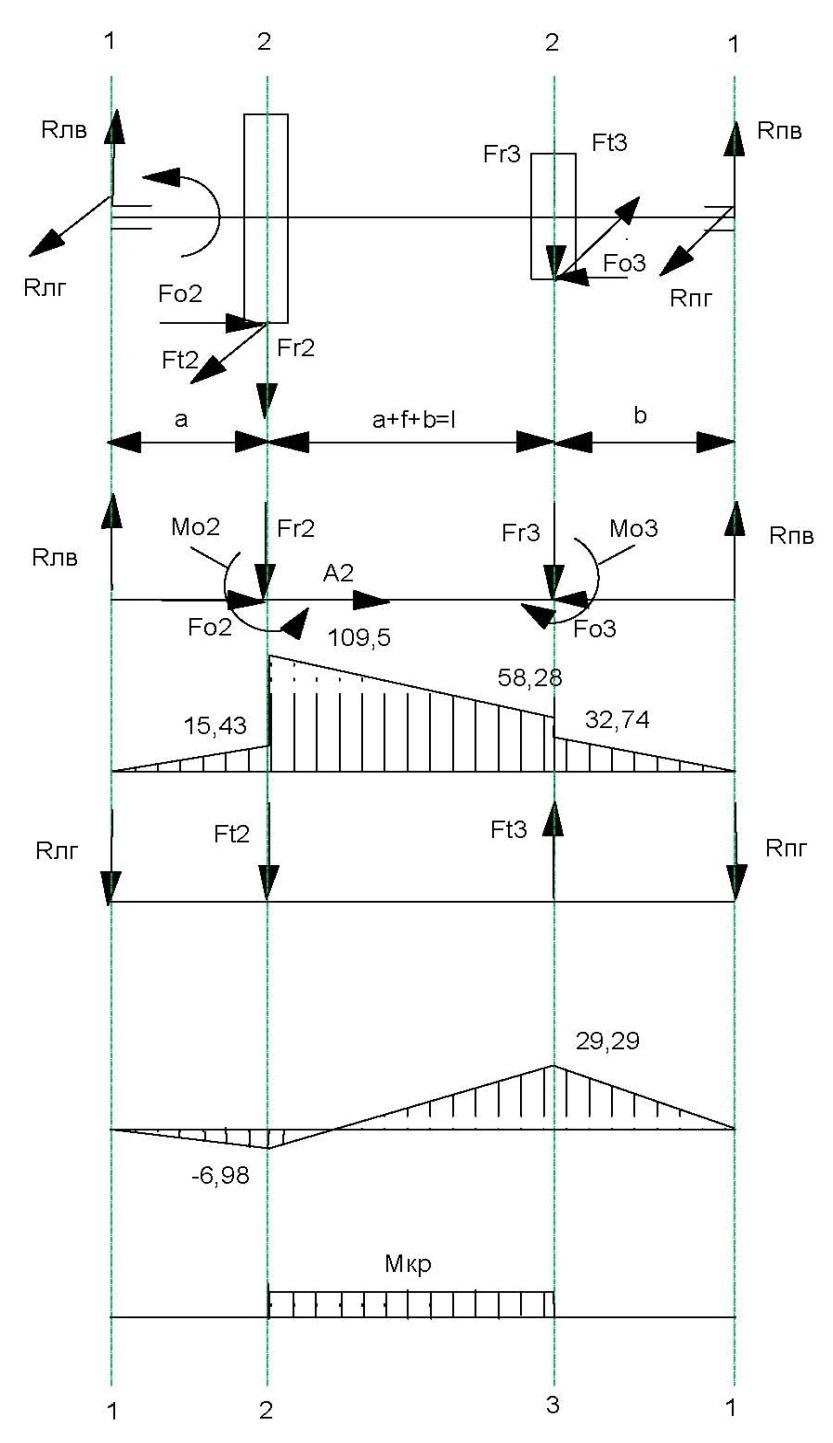
Рисунок 11.2

Расчет реакций в опорах и изгибающих моментов в вертикальной плоскости:

- момент от осевой силы

==144,54·0,23124/2=16,7Н·м

-момент от осевой силы :

==483,96·0,04837/2=11,7Н·м

-осевая реакция

=-=144,54-483,96=-339,42Н

-сумма моментов действующих сил относительно левой опоры Л:

∑=·a+( + +b)=0

откуда

=(·a+ ( + +b)=

(-16,7+11,7+194,7∙0,038+938,95∙0,1435)/0,1885=727,52Н

-сумма моментов действующих сил относительно правой опоры П:

∑=--(а+ +с)=0

= (- ·+ ( + +b) =

=(-11,7+16,7+194,7∙0,1505+938,95∙0,045)/0,1885=406,13Н

Проверка:+--=727,52+406,13-938,95-194,7=0

-изгибающий момент в сечении 2 (слева):

=∙ = 406,13∙0,038=15,43 Н∙м

-изгибающий момент в сечении 2 (справа):

=∙= 727,52∙0,1505=109,5 Н∙м

-изгибающий момент в сечении 3 (слева):

=∙ = 406,13∙0,1435=58,28 Н∙м

-изгибающий момент в сечении 2 (справа):

=∙ = 727,52∙0,045=32,74 Н∙м

Расчет реакций в опорах и изгибающих моментов в горизонтальной плоскости.

-сумма моментов действующих сил относительно левой опоры Л:

∑=∙-∙(+-( + +b)=0

откуда ∙-∙(+))/ ( + +b)=(527,53∙0,038-2533,8∙0,1435)/0,1885=-1822,55Н

-сумма моментов действующих сил относительно правой опоры П:

∑=∙∙(++( + +b)=0

откуда =∙∙(+/( + +b)=(-2533,8∙0,045+527,53∙0,1505)/0,1885=-183,72Н

Проверка:-++=2533,8-527,53-1822,55-183,72=0

-изгибающий момент в сечении 2 вала:

=∙=-183,72∙0,038=-6,98 Н∙м

-изгибающий момент в сечении 3 вала:

=∙=-26,36+55,65=29,29

Равнодействующая реакция:

-в левой опоре

∑ =Н

-в правой опоре

∑ =Н

-осевая в левой опоре

A=-=483,96-144,54=339,42Н

Равнодействующий изгибающий момент:

-в сечении 2

∑ =Н

-в сечении 3

∑ =Н

3. Выходной вал:

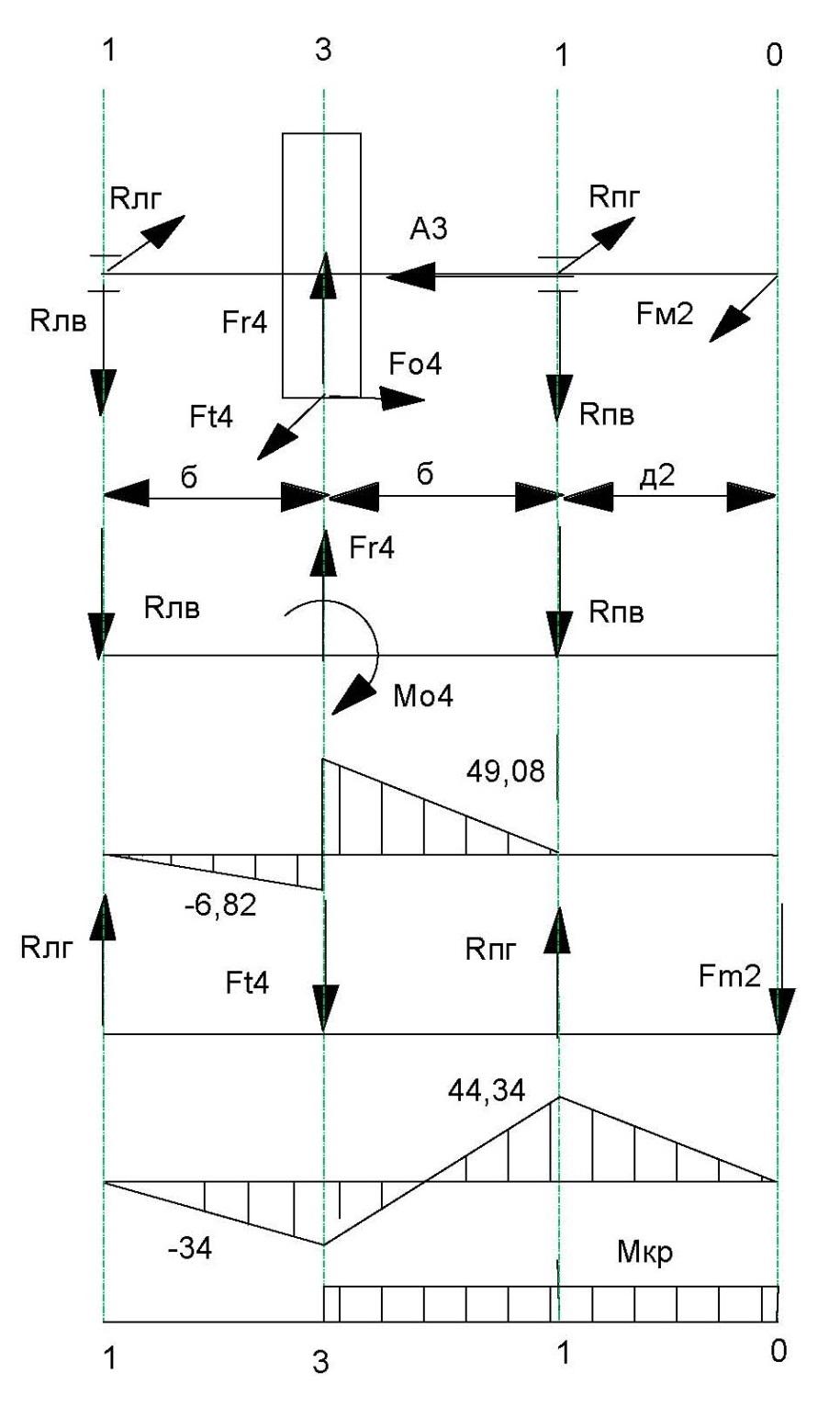
Рисунок 11.3

Силы, действующие в зацеплении:

окружная: F_t4=2533,8Н;

радиальная: F_r4=938,95 Н;

осевая: F_o4=483,96 Н;

F_M2 =0,1· F_t4 =0,1∙2533,8=253,38Н

l _в2 =3,5·d_3-3=3,5∙50=175=0,175м

Расчет реакций в опорах и изгибающих моментов в вертикальной плоскости:

- момент от осевой силы F_о1

M_o4= F_o4∙ d_д4/2= 483,96 ∙0,231/2=55,9Н·м

-осевая реакция

А₃=- F_o4 = -483,96 Н

-сумма моментов действующих сил относительно левой опоры Л:

∑ = -M_o4- F_r4∙ а + ∙2а =0

откуда =( F_r4∙б+M_o4)/2б=(938,95∙0,045+55,9)/0,09=1090,6Н

-сумма моментов действующих сил относительно правой опоры П:

∑ = -M_o1+F_r4∙ б - ∙2б =0

Откуда =( F_r4∙б- M_o4)/2б=(938,95∙0,045-55,9)/0,09=-151,64Н

Проверка: F_r4 - - =938,95-1090,6-(-151,64)=0

-изгибающий момент в сечении 3(слева)

=∙б=-151,64∙0,045=-6,82Н·м

-изгибающий момент в сечении 3(справа)

=∙б=1090,6∙0,045=49,08Н·м

Расчет реакций в опорах и изгибающих моментов в горизонтальной плоскости:

-сумма моментов действующих сил относительно левой опоры Л:

∑ = F_м2∙( д₂+2б) +F_t4∙ б - ∙2б =0

Откуда =( F_t4∙ б + F_м2∙(д+2б))/2б=(67,15+114,02)/0,09=2013 Н

-сумма моментов действующих сил относительно правой опоры П:

∑ = -F_t4∙ б + ∙2б +F_м2∙ д₂ =0

Откуда =( F_t4∙ б - F_м2∙ д₂)/2б=(114,02-44,34)/0,09=774,18

Проверка : +- F_t4 - F_м2=2013+774,18 -2533,8-253,38=0

-изгибающий момент в сечении 3 вала:

=-∙б=∙а=-774,18∙0,045=-34,83Н·м

-изгибающий момент в сечении 1 вала:

=∙2б + F_t4∙ б=-69,68+114,02=44,3 Н·м

Равнодействующая реакция:

- в левой опоре

∑ R_л===788,9Н

- в правой опоре

∑ R_п===2289,45Н

-осевая в левой опоре

A= F_o4=483,96 Н.

Равнодействующий изгибающий момент:

-в сечении 1

M_и1= = F_м2∙ д₂=253,38∙0,175=44,34 Н·м

-в сечении 3

∑ M_и3===35,2 Н·м