
- •II. Функції
- •2.1 Поняття функції. Способи задання функцій
- •Приклади для самостійного розв’язання
- •13. . 14..
- •Приклади для самостійного розв’язання
- •2.3 Складна функція
- •Приклади для самостійного розв’язання
- •4. . 5.
- •2.4 Обернена функція
- •Приклади для самостійного розв’язання
- •2.5 Основні елементарні функції
- •2.6 Елементарні функції
- •Основні способи побудування графіків функцій
- •Приклади для самостійного розв’язання.
Приклади для самостійного розв’язання
Дана функція
 Знайти :f(0),
f(3),
f(4),f(-1),
f(2-
Знайти :f(0),
f(3),
f(4),f(-1),
f(2- ),
f(а-1),
f(а)-1.
),
f(а-1),
f(а)-1.Знайти
 -
лінійну функцію, якщоf(0)=-6
і f(4)=2.
-
лінійну функцію, якщоf(0)=-6
і f(4)=2.Знайти квадратичну функцію
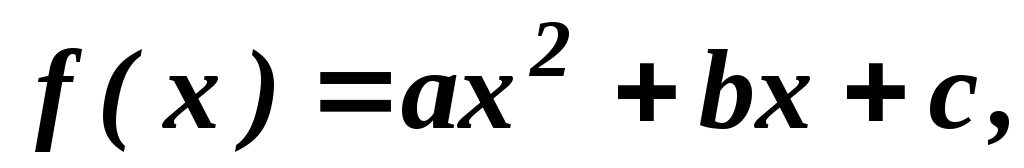 якщоf(0)=4,
f(1)=2,
f(2)=6.
якщоf(0)=4,
f(1)=2,
f(2)=6.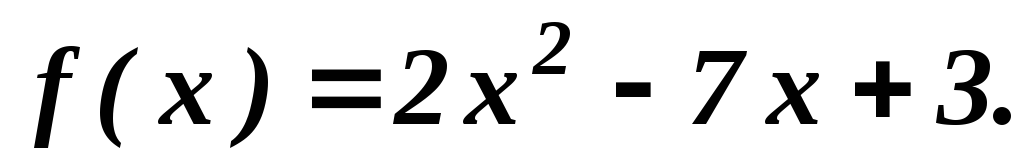 Знайти
корені рівнянь: f(х)
=
f(0),
f(х)=
f(2).
Знайти
корені рівнянь: f(х)
=
f(0),
f(х)=
f(2).Визначити функцію третього степеня
![]() Якщо
f(-1)=-8,
f(0)=1,
f(1)=2,
f(2)=7.
Якщо
f(-1)=-8,
f(0)=1,
f(1)=2,
f(2)=7.
Дана функція
 Знайти корені рівнянняf(х)=0.
Знайти корені рівнянняf(х)=0. Знайти
Знайти
 і
і

8.
Відомо,
що
![]() .
Знайти
.
Знайти![]() ,
,![]() .
.
9.
Дано
![]() .
Знайти
.
Знайти![]() .
.
10.
Дана функція
![]() .
Знайти:
.
Знайти:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
11.
Дано
![]() .
Знайти
.
Знайти![]() .
.
12.
Дана функція
![]() .
Знайти
.
Знайти![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Визначити область існування таких функцій:
13. . 14..
15.
![]() .
16.
.
16.![]() .
.
17.
![]() .
18.
.
18.![]() .
.
19.
![]() .
20.
.
20.![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
Відповіді:
1; -2; 1; 6; 0;
 ;
; .
. .
. .
.а) 0; 3,5. б) 2; 2,5.
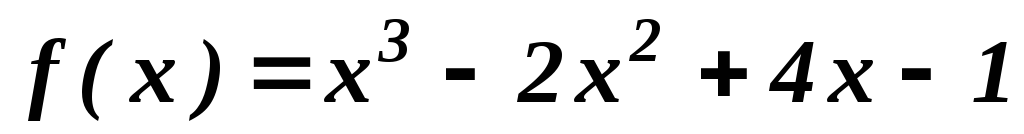 .
.–2; -1; 1.
 ,
,
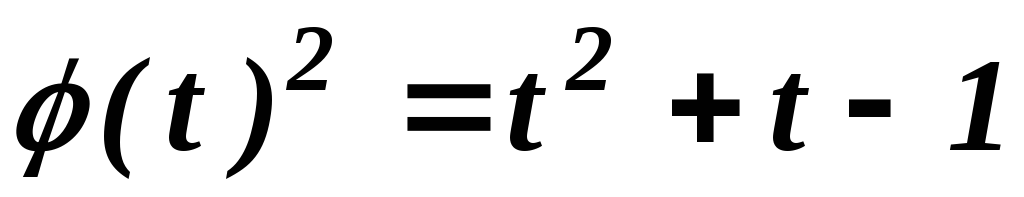 .
. ;
;
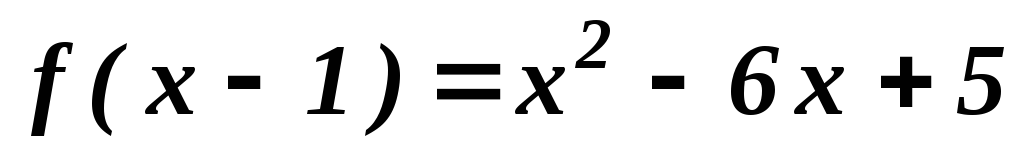 .
.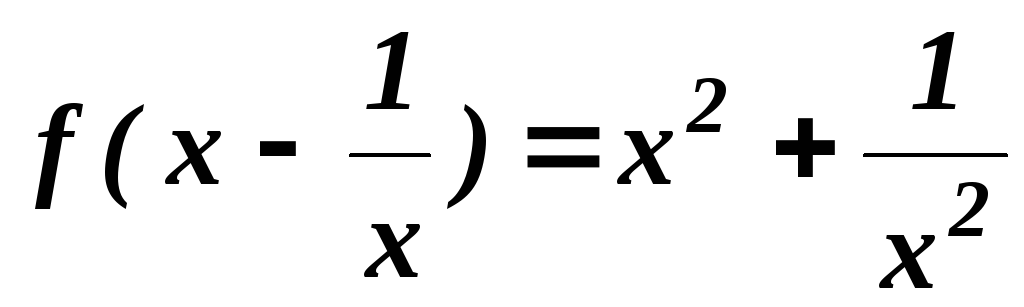 .
.–1; 0;
 ;
;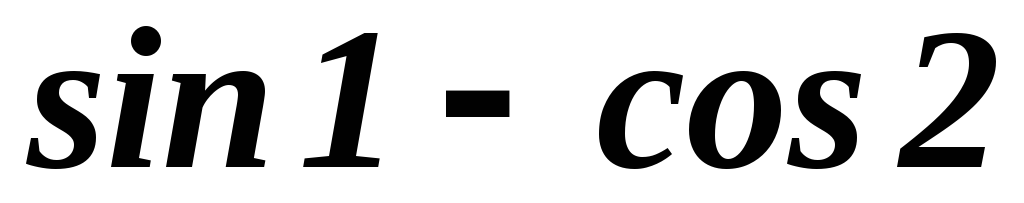 ;
2.
;
2. .
. ;
;
 ;
; ;
; ;
; -
неіснує.
-
неіснує. .
.
 .
. .
. .
. .
. .
. .
. .
.
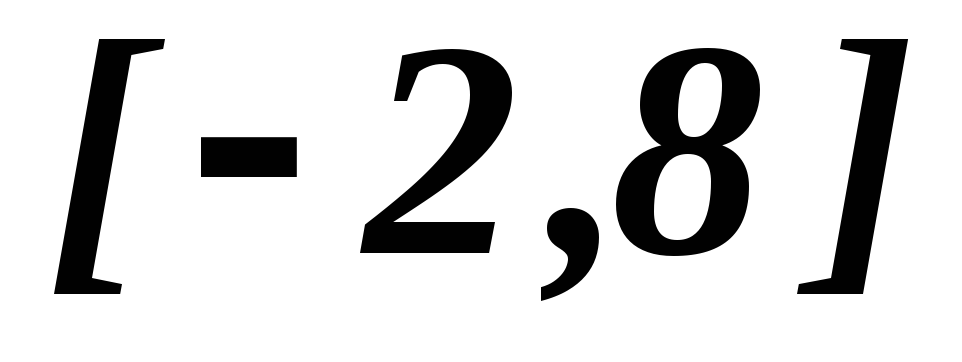 .
. ,
,

Побудувати графік (по точках) таких функцій:
а)
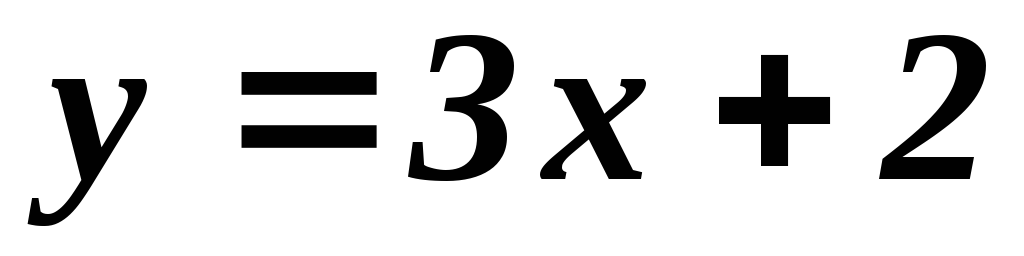 ;
б)
;
б) ;
в)
;
в) .
.а)
 ;
б)
;
б)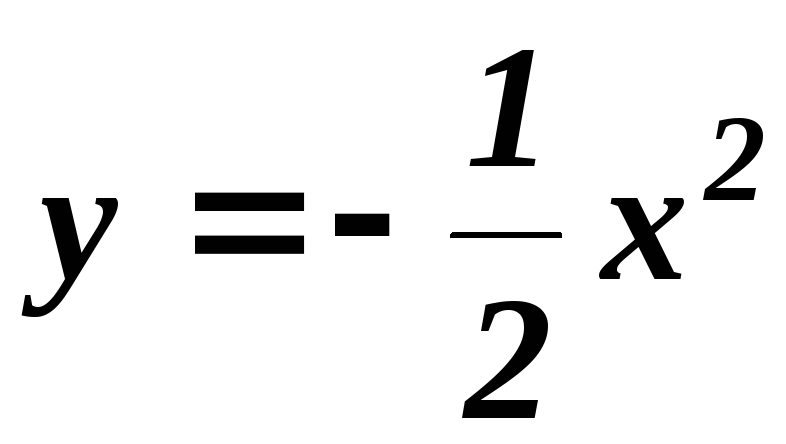 ;
в)
;
в) ,г)
,г)
 ;
д)
;
д)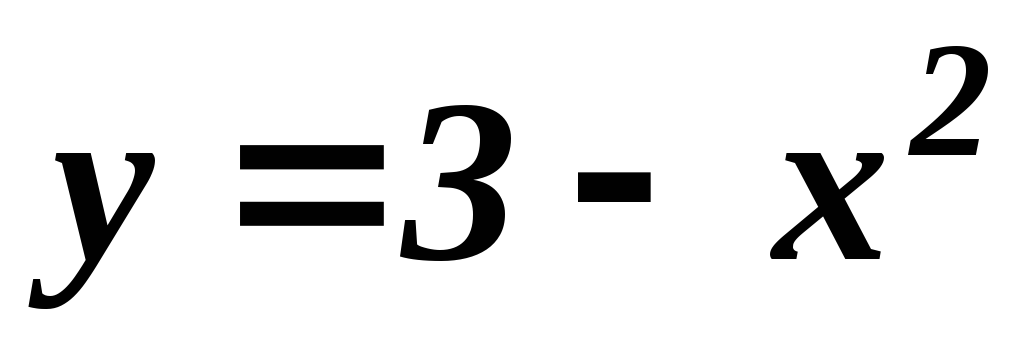 ;е)
;е)
 .
.а)
 ;
б)
;
б) ;
в)
;
в) ;г)
;г)
 ;
д)
;
д) .
.
27.

28.

2.2 Монотонні функції
Означення.
Функцію
![]() ,
визначену на інтервалі
,
визначену на інтервалі
![]() ,
називають:
,
називають:
зростаючою,
якщо із нерівності
![]() випливає нерівність
випливає нерівність
![]() ;
;
спадною,
якщо із нерівності
![]() випливає нерівність
випливає нерівність
![]() ;
;
неспадною,
якщо із
![]()
![]()
![]() ;
;
незростаючою,
якщо із
![]()
![]()
![]() .
.
Кожну із таких функцій називають монотонною, а функції зростаючі і спадні називають строго монотонними.
Часто
функція, задана на деякому інтервалі,
не є монотонною, але цей весь інтервал
можна розбити на такі окремі інтервали,
що на кожному з них функція
![]() буде монотонною (див. рис. 5).
буде монотонною (див. рис. 5).

Y

![]()
![]()
![]()
![]()
![]()
![]()
Рис.5
На
кожному з інтервалів
![]() ,
,
![]() ,
,
![]() – функція монотонна.
– функція монотонна.
Зауважимо, що існують функції, які немонотонні ні на якому інтервалі, наприклад, функція Діріхле.
Приклади. Знайти проміжки зростання та спадання функцій, а також найбільше й найменше значення (якщо вони існують):
1.
![]() .
.
Розв’язання.
Функція
існує для всіх
![]() .
Нехай
.
Нехай![]() ,
тоді
,
тоді![]() ,
тобто функція
,
тобто функція![]() -
зростає (скорочено
-
зростає (скорочено![]() ).
).
2.
![]() .
.
Розв’язання.
Дана
функція не існує у точці
![]() ,
ії область існування складається з
проміжків
,
ії область існування складається з
проміжків![]() і
і![]() .
.
На
проміжку
![]()
![]() -
спадає (скорочено
-
спадає (скорочено
![]() ).
Дійсно, нехай
).
Дійсно, нехай
![]() і
і
![]() ,
тоді віднявши від обох частин нерівності
число 3, отримаємо
,
тоді віднявши від обох частин нерівності
число 3, отримаємо![]() ,
а для обернених величин знак нерівності
змінюється на протилежний, тобто
,
а для обернених величин знак нерівності
змінюється на протилежний, тобто
![]() ,
а це означає
,
а це означає![]() ,
функція – спадає
,
функція – спадає
Аналогічно
для
![]() і
і
![]() маємо
маємо
![]()
![]() спадає
спадає
3.
![]()
Розв’язання.
Виділимо у заданому виразі
![]() повний
квадрат
повний
квадрат

тоді
![]()
Нехай
![]() і
і
![]() тоді
тоді![]() Оскільки
Оскільки![]() то
із нерівності
то
із нерівності![]()
![]()
тобто
функція
![]() – зростає.
– зростає.
Аналогічно
для
![]() і
і
![]()
![]()
![]()
функція спадає.
При
![]()
![]() ,
,![]() – найбільше
значення функції.
– найбільше
значення функції.
Приклади для самостійного розв’язання
Для поданих нижче функцій знайти проміжки зростання і спадання, а також найбільше і найменше значення (якщо вони існують):
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]() 5.
5.
![]() 6.
6.
![]()
Відповіді:
1.
Спадає на
![]() ,
зростає на
,
зростає на![]() ,
,![]() – мінімум прих=2,
f(2)=5
– min.
– мінімум прих=2,
f(2)=5
– min.
2.
Зростає на
![]() ,
спадає на
,
спадає на![]() ,f(-6)=4
– максимальне
значення. 3.
Зростає на
,f(-6)=4
– максимальне
значення. 3.
Зростає на
![]() і на
і на![]() .4.
Зростає на
.4.
Зростає на
![]() .5.
Спадає на
.5.
Спадає на
![]() .6.Зростає
на
.6.Зростає
на
![]() ,
,![]() Спадає на
Спадає на![]() ,
,![]()
При
![]() –
максимум;
–
максимум;
при
![]() – мінімум.
– мінімум.
