bludova_t_v_praktikum_z_vishoi_matematiki

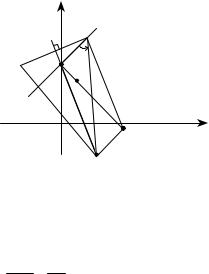
Знайти:

а) рівняння третьої сторони ВС; б) відстань від точки В до прямої АС;

в) кут В в радіанах з точністю до двох знаків; г) точку перетину висот трикутника.

ЕO

АМ у відношенні DMAD 23 . Щоб знайти рівняння ВС, необхідно

знайти координати точок В і С, які можна знайти, знаючи рівняння прямих ВD і DC. Для відшукання рівняння прямої ВD потрібно знайти координати точки D і використати умову паралельності прямих АС і ВD. Аналогічно знаходимо рівняння СD.

1) Знаходимо координати точки D:

Маємо D (3, –1).

198

2)ВD: BD AC 3x y n 0. Точка D лежить на прямій ВD, тому 3 3 1 n 0, n 8. 3x y 8 0 — рівняння ВD.

3)Знаходимо координати точки В. Для цього можна розв’язати систему рівнянь методом Крамера:

Координати точки В: xB 3022 1511 , yB 1143 .

4) Аналогічно попередньому визначаємо координати точки С:

CD: CD AB 7x 5y n 0.

Точка D лежить на прямій СD, звідки випливає, що 7 3 5 1 n 0 , n 26 ; 7x 5y 26 0 — рівняння прямої СD.

5) Знаходимо координати точки С. Для цього потрібно розв’язати систему

6) Рівняння прямої ВС знаходимо як рівняння прямої, яка проходить через дві точки:

199

11y 43 25 11x 11y 418 0 25x y 38 0.

Рівняння ВС: 25x y 38 0.

б) Відстань від точки В до прямої АС знаходимо за формулою

BH d Ax0 By0 C ,

A2 B2

де Ах + Ву + С = 0 — рівняння прямої АС; х0, у0 — координати точки В.

Відстань від точки В до прямої АС дорівнює 3510 . в) Кут В знаходимо за формулою

tg B k1 k2 , 1 k1k2

де k1 — кутовий коефіцієнт прямої АВ, а k2 — кутовий коефіцієнт прямої ВС; k1 75 , k2 25.

B arctg 0,7941 0,6711.

B 0,6711 рад.

200

11114

2 55 134 4796.

Точка перетину висот Р (– 4,95; 1,80).

Задача 2.2-2. Відомі координати двох вершин А (–1, 3), В (7, 1) і точка перетину висот М (6, 3). Знайти:

а) рівняння його сторін; б) координати третьої вершини С; в) тангенс кута А;

г) довжину висоти ВD;

201

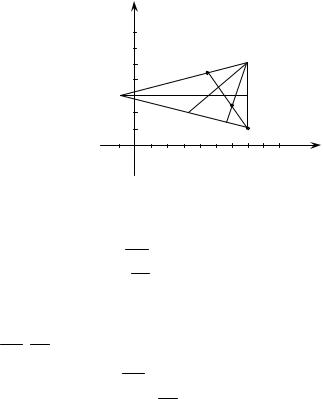
д) площу трикутника S ABC 12 BD AC ; е) точку перетину медіан.

y

DС

АT Q

а) Спочатку зробимо рисунок. Знайдемо рівняння висот. ВС: АМ ВС. Розглядаючи їх як вектори, маємо AM BC 0 ,

або, у координатній формі:

AM 6 1 ,3 3 7,0 ,

BC x 7 0 y 1 , 7 x 7 0 y 1 0, x 7 .

АС: АС ВМ, розглядаючи ці відрізки як вектори, маємоBM AC 0 , або, у координатній формі:

BM 6 7, 3 1 1, 2 ,

AC x 1, y 3 ,

1 x 1 2 y 3 0 x 1 2 y 6 0 .

Звідси x 2 y 7 0.

У нашому випадку

x1 1, y1 3, x2 7, y2 1.

202

Маємо

АС: x 2 y 7 0 ; ВС: x 7 ; АВ: x 4 y 11 0 .

б) Через вершину С проходять дві прямі АС і ВС. Щоб знайти координати цієї вершини, потрібно розв’язати систему

Координати вершини С (7, 7). в) Скористаємось формулою

г) Довжина висоти ВD дорівнює відстані від точки В до прямої АС і обчислюється за формулою:

д) ВD обчислено в п. г. Знайдемо АС.

AC xC xA 2 yC yA 2 7 1 2 7 3 2 64 16

80 4 5.

203

е) Знайдемо координати точки Q — середини відрізка ВС:

Точка Т перетину медіан поділяє медіану AQ у відношенні

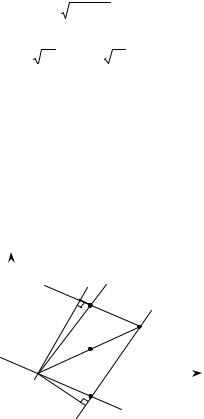
Задача 2.2-3. Рівняння однієї зі сторін квадрата 2х + 3у – 4 = 0. Точка перетину діагоналей М (2, 2).

Знайти:

а) довжину сторони АD квадрата; б) рівняння сторін квадрата.

y C

N R

M D

а) AD 2ME — відстань від точки М до прямої АВ.

Звідси AD 12 13 . 13

204

б) Достатньо знайти координати вершин В і D. Складаємо рівняння сторони ВD, знаходимо координати точки В (точка перетину прямих АВ і ВD) і, знаючи точки В і М, визначаємо точку D. Рівняння прямої ВD шукаємо у вигляді y yM kBD x xM .

Коефіцієнт kBD обчислюємо з рівняння:

ВС: рівняння прямої ВС шукаємо у вигляді прямої, яка проходить через дану точку в даному напрямі: y yB kBC x xB . Кое-

205

Маємо:

СD: пряма CD AB проходить саме через точку D. Шукаємо рівняння СD у вигляді y yD k AB x xD ,

2x 3 y 16 0 .

АD: Пряма AD BC і проходить через точку D. Тому її рівняння

Зауваження

Рівняння сторін квадрата можна знайти простіше, скориставшись формулою для відстані від точки М (точка перетину діагоналей) до сторін АВ і СD, АD i BC.

Рівняння СD: 2x 3y 16 0, AB : 2x 3y 4 0 .

206

дорівнюють МЕ.

Рівняння сторін AD i BC мають такий вигляд: 2x 3y 4 0 і 2x 3y 8 0.

Задача 2.2-4. Відоме рівняння двох сторін паралелограма ABCD. AD: 2x 4 y 2 0 ; AB: 3x 2 y 3 0 . Діагоналі паралелог-

рама перетинаються в точці М (3, 1).

Зобразимо на площині прямі АD і АВ, точку М (3, 1), а також паралелограм.

а) рівняння діагоналей;

б) довжини висот AT i AR паралелограма, що дорівнюють відстані від точки А до прямих BC i DC;

в) кут BAD;

г) площу паралелограма;

д) рівняння висоти AF, опущеної з точки А на діагональ BD.

207