Лабораторная работа № 2 Определение коэффициента трения в резьбовом соединении

Цель работы: расчётно-экспериментальным путем определить коэффициент трения и другие характеристики затянутого резьбового соединения.

Оборудование и инструмент: лабораторный стенд ДМ27М (рис. 2.1) с набором деталей резьбового соединения, штангенциркуль, шаблон резьбовой, динамометрический гаечный ключ.

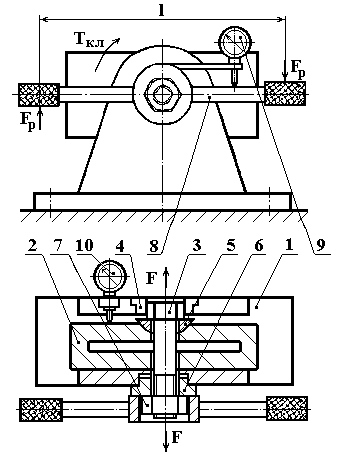
Рис. 2.1. Конструктивная схема лабораторного стенда ДМ27М:

1 – станина; 2 –динамометрическая скоба; 3 – болт; 4 – стопорная скоба;

5 - сферическая шайба; 6 – стопорная шайба; 7 – гайка; 8 – динамометрический ключ;

9 – индикатор динамометрического ключа; 10 - индикатор динамометрической скобы.

1. Теоретические основы работы

Согласно теории винтовой пары [1] при затяжке резьбового соединения вращающий гайку момент на ключе идет на преодоление моментов сопротивления от сил трения в резьбеи на торце гайки, т.е.

, (2.1)

где , (2.2)

. (2.3)

В свою очередь , (2.4)

, (2.5)

, (2.6)

где - осевая сила (сила затяжки), возникающая в стержне болта при затяжке резьбового соединения, Н;- средний диаметр метрической резьбы, мм;- номинальный диаметр резьбы, мм;- шаг резьбы, мм;- угол трения в резьбе, град.;- коэффициент трения в резьбе и на торце гайки;- угол профиля метрической резьбы;- угол подъема винтовой линии резьбы, град;- средний диаметр опорного торца гайки, мм;- внешний диаметр опорного торца гайки, мм;- размер гайки под ключ, мм;- диаметр отверстия в стопорной шайбе с прямоугольным выступом, мм.

Подставив (2.2) и (2.3) с учетом (2.4), (2.5) и (2.6) в (2.1), получаем базовое для решения поставленной в работе задачи уравнение

. (2.7)

Очевидно, что коэффициент трения в резьбовом соединении можно определить, решив уравнение (2.7) при известных значениях всех его остальных членов.

2. Порядок выполнения работы и оформление её результатов

1. Изучают теоретические основы работы.

2. С помощью штангенциркуля и резьбового шаблона проводят опытные замеры геометрических характеристик деталей резьбового соединения: ,,,и записывают значения этих параметров.

3. Используя приведенные выше расчетные зависимости, вычисляют значения параметров и.

4. Исходя из условия прочности установленного с зазором и затянутого болта без дополнительной нагрузки [1]

, (2.8)

где - эквивалентные напряжения;- допускаемые напряжения растяжения материала болта;- предел текучести материала исследуемых в работе болтов из углеродистой стали (типа сталь 3);- допускаемое значение коэффициента запаса прочности;- внутренний диаметр резьбы болта, рассчитывают экспериментальное значение силы затяжки соединения по формуле

(2.9)

при - коэффициент уменьшения в ходе эксперимента максимально допустимой силы затяжки.

5. Значение момента на ключе , необходимое для получения экспериментальной силы затяжки резьбового соединения, определяют опытным путем на стенде ДМ27М (рис. 2.1). При этом значение , пропорциональное деформации плоской динамометрической скобы 2, фиксируют по показаниям индикатора 10. В делениях прибора значениесоставит

, (2.10)

где - коэффициент пропорциональности.

Искомое значение , пропорциональное деформацииU-образной скобы динамометрического ключа 8, определяют при затяжке соединения по показаниям индикатора 9 в момент, когда стрелка индикатора 10 отклоняется на число делений, рассчитанное по (2.10). Результаты неоднократных измерений (не менее 5) момента в делениях прибора заносят в табл. 2.1 и рассчитывают их среднее значение по формуле

, (2.11)

где - число измерений. Окончательно величинуопределяют как

, (2.12)

где - коэффициент пропорциональности.

Таблица 2.1

Результаты эксперимента

, Н	, дел.	, дел.	, дел.	, дел.	, дел.	, дел.	, дел	, Нм

6. Подставив все найденные значения параметров в базовое уравнение (2.7), решают его относительно искомого коэффициента трения 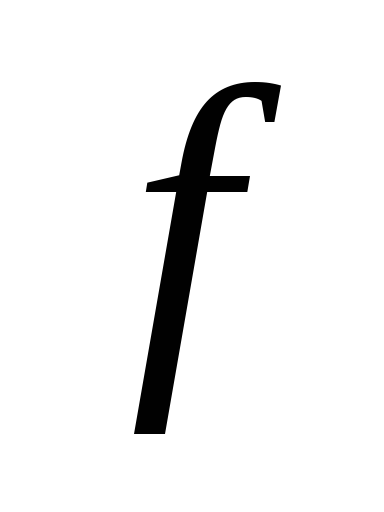в исследуемом резьбовом соединении.

Сначала уравнение (2.7) преобразуют к удобному для дальнейшего решения виду

, (2.13)

где ; ;;- константы уравнения.

Затем используют аналитический или графический метод решения уравнений.

Первый метод сводится к преобразованию зависимости (2.13) в квадратное уравнение с применением известной формулы для тангенса суммы двух улов и решению этого уравнения, один из корней которого даст значение искомого коэффициента трения , а второй не будет иметь физического смысла.

При втором методе строят графики функций левой и правой частей уравнения в возможном при сухом контакте стальных поверхностей диапазоне значений (рис. 2.2).

Рис. 2.2. Графическое решение базового уравнения

Решением уравнения (2.13) является значение аргумента, соответствующее точке пересечения графиков и . Опустив перпендикуляр из этой точки на ось абсцисс, получают искомое значение коэффициента трения в резьбовом соединении.

7. Для проверки результатов аналитического или графического решения уравнения и определения других характеристик затянутого резьбового соединения используют компьютерную программу «Rezba_Lab».

Форма вводимых в интерактивном режиме работы исходных данных и получаемых результатов расчёта представлена на рис. 2.3.

Рис. 2.3. Исходные данные и результаты расчёта программы «Rezba_Lab»