2) Якщо в усіх точках проміжку (а, с) друга похідна від’єм­на , то графік функції випуклий.

Теорема 2. Якщо для функції друга похідна їїу деякій точціх₀ перетворюється на нуль або не існує й при переході через цю точку змінює свій знак на обернений, то точка є точкою перегину графіка функції.

66. Точки перегину графіка функції. Необхідна і достатня умови існування точок перегину

Т., яка відокремлює опуклу частину кривої від вгнутої, наз. т. перегину.

Якщо т. х₀ є т. перегину графіка, f’’(x)=0 або не існує.

Теорема 1. Якщо для ф-ції f(x) друга пох. її f’’(x) у деякій т. x₀ перетвор. на 0 або не існує й при переході через цю т. змінює свій знак на обернений, то т. М(х₀, f(x₀)) є т. перегину.

67. Асимтоти графіка функції

Пряма називається асимптотою кривої, якщо відстань d від змінної точки М кривої до цієї прямої при віддаленні точки М у нескінченність прямує до нуля (4.18). Асимптоти бувають вертикаль­ні й похилі.

Вертикальні асимптоти. Якщо

, або ,

або , то прямах = а є вер- тикальною асимптотою для графіка функції .

Похилі асимптоти. Нехай крива має похилу асимптоту, тоді

. (4.20)

Якщо хоча б одна з границь (4.20) не існує, то крива похилих асимптот у відповідній напівплощині не має.

68. Функції кількох змінних. Основні поняття

69. Функції двох змінних. Область визначення

Згідно з означенням функцію можна розглядати як функцію точки і записувати.

Зокрема, при n = 2 говорять, що задана функція двох змінних , якщо кожній паріна площині поставлено у відповідність тільки одне числоz. Cукупність усіх впорядкованих наборів чисел виду (х,у), при яких функція z=f(x,y) приймає певні дійсні значення, називають областю визначення функції. Знаходження області визначення функції двох змінних

Покажемо алгоритм знаходження області визначення функції двох змінних на прикладі.

Приклад. Знайти область визначення функції та надати їй геометричну інтерпретацію.

1. Знайдемо область визначення функції аналітично

.

2. Нерівності в D замінюємо рівностями і будуємо лінії, що їм відповідають на координатній площині, а саме: ;.

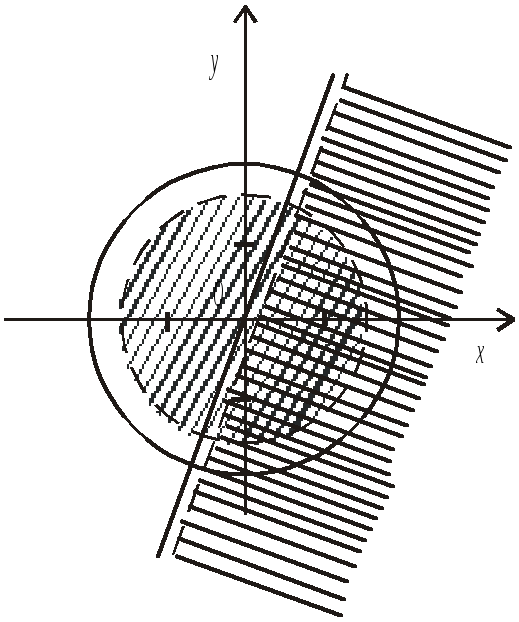
Рис. 5.9

3. Визначаємо за допомогою контрольних точок ,розміщення D на площині і заштриховуємо її (рис. 5.9).

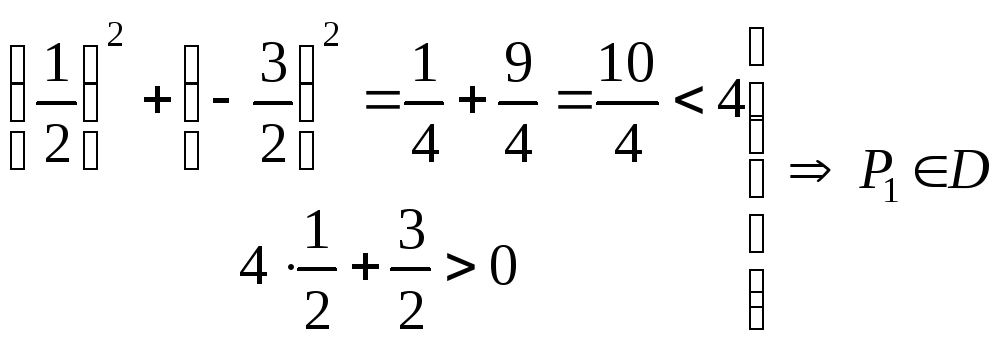
70. Лінії рівня функції двох змінних

71. Частинний приріст і частинні похідні І-го порядку

Різницю називаютьчастинним приростом за х, а різницю —частинним приростом за y функції ; їх позначають відповідноі. Таким чином,

,

Якщо існує , то її називають частинною похідною функції z=f(x,y) по змінній х і позначаютьабо

,

72. Повний приріст і повний диференціал функції двох змінних

73. Використання повного диференціала до наближених обчислень

Використання диференціала для наближених обчислень знаходится за формулою:

Похідна за напрямом

Відомо, що механіч. зміст похідної ф-ції 1 незалеж змінної – змінювання ф-ції в даний момент х. Аналогічно можна тлумачити мех. зміст частин похідних І-го порядку ф-ції z=f(x;y)

z/x – швидкість зміни ф-ції в напрямі Ох.

z/y - швидкість зміни ф-ції в напрямі Оу.

Частин похідну ф-ції z не залеж змінної за напрямом ех, еу знаходять:

де  і  - кути, які утвор. Вектор е з осями координат.

74. Градієнт функції Z=f(x,y)

Вектор з координатами , який характеризує напрям максимального зростання функціїу точці, називається градієнтом функції у цій точці і позначається(— одиничні орти):

Похідна за напрямом функціїта градієнт пов’язані співвідношенням

75. Частинні похідні вищих порядків. Теорема про рівність мішаних похідних

Частинну похідну першого порядку по змінній від частинної похідної першого порядку по зміннійназивають частинною похідною другого порядку функції по зміннійтаі позначають :або

Теорема: якщо функція z=f(x;y) та похідні та неперервні в точці (х;у) та в деякому її околі, то в цій точці

76. Знаходження екстремуму функції кількох змінних

Алгоритм дослідження функції на екстремум

1. Знайти перші частинні похідні та.

2. Знайти стаціонарні точки, тобто точки, в яких ,.

3. Знайти частинні похідні другого порядку ,,.

4. Обчислити значення частинних похідних другого порядку в стаціонарних точках.

5. Для кожної стаціонарної точки знайти і зробити висновки на базі теореми:

Нехай функція має екстремум у точцінеперервні частинні похідні першого й другого порядку, причомута, а також,,. Якщо: