
- •1. Якщо — н.М.В. І, то обернена до неї послідовністьбуде н.В.В., і навпаки.
- •2. Якщо yn — н.В.В., то обернена до неї — н.М.В.
- •3. Невизначеність
- •4. Невизначеність
- •4.1.2. Геометричний зміст похідної
- •2) Якщо в усіх точках проміжку (а, с) друга похідна від’ємна , то графік функції випуклий.
- •1) І, тодіточка максимуму функції;
- •2) І, тодіточка мінімуму функції;
- •3) , Тоді в точцінемає екстремуму.
- •4) , Тоді потрібні додаткові дослідження
Матриці, основні поняття. Різновиди матриць
Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д.
Типи матриць:
Якщо кількість рядків матриці дорівнює кількості її стовпців, то матриця називається квадратною. Квадратну матрицю розміром п на п називають матрицею п-го порядку.
Квадратна матриця у якої всі елементи крім елементів головної діагоналі дорівнюють 0 називається діагональною матрицею.
Квадратна матриця, в якої елементи головної діагоналі дорівнюють одиниці, а всі інші нулю називається одиничною матрицею, і позначають Е.
Квадратна матриця називається трикутною, якщо всі елементи, розміщені по один бік від головної діагоналі, дорівнюють 0.
Матрицю, у якої всі елементи дорівнюють 0 називають нульовою і позначають О.
Матриця, яка складається з одного стовпця називається матрицею-стовпцем, а яка складається з одного рядка – матрицею-рядком.
Матриця розміром 1 на 1 означає те число.\
Дії над матрицями. Властивості дій над матрицями
Сумою матриць
одного й того самого порядку
![]() і
і
![]() називається матриця
називається матриця![]() ;
;![]() ,
будь-який елемент якої дорівнює сумі
відповідних елементів матриць
А
і В:
,
будь-який елемент якої дорівнює сумі
відповідних елементів матриць
А
і В:
![]() .
Наприклад обидві матриці
.
Наприклад обидві матриці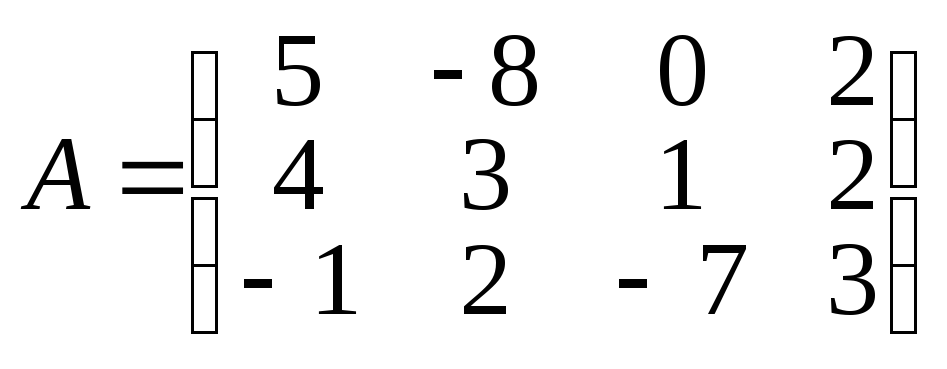 ,
, мають розмір
мають розмір![]() ,
тому за означенням можна утворити їх
суму — матрицю
,
тому за означенням можна утворити їх
суму — матрицю
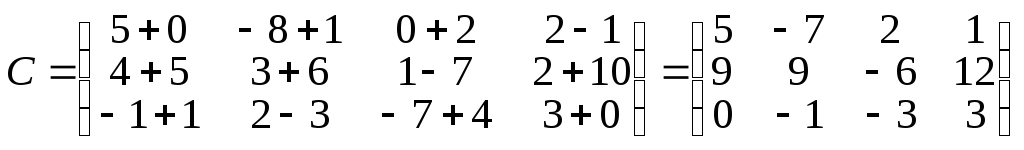 .
.
Добутком матриці
![]() на деяке число
на деяке число
![]() називається такаматриця
С,
кожен елемент якої
називається такаматриця
С,
кожен елемент якої
![]() утворюється множенням відповідних
елементів матриці А
на
утворюється множенням відповідних
елементів матриці А
на
![]() ,
,![]() .
.
Очевидно, що для суми матриць і добутку матриць на число виконуються рівності:
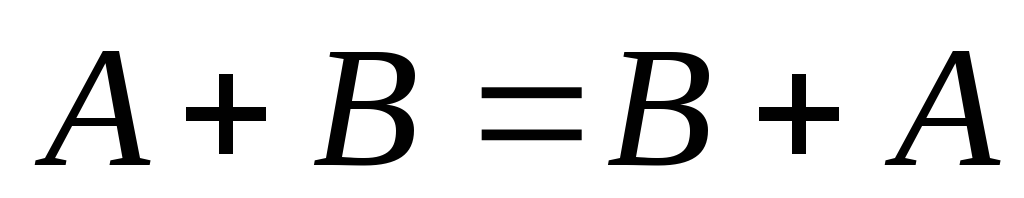 ;
2)
А+(В+С)=(А+В)+С; 3) А+0=А; 4) А-А=0; 5) к(А+В)=кА+кВ;
6) (к+р)А=кА+кВ; 7) к(рА)=(кр)А
;
2)
А+(В+С)=(А+В)+С; 3) А+0=А; 4) А-А=0; 5) к(А+В)=кА+кВ;
6) (к+р)А=кА+кВ; 7) к(рА)=(кр)АДобутком матриці
 розміру
розміру
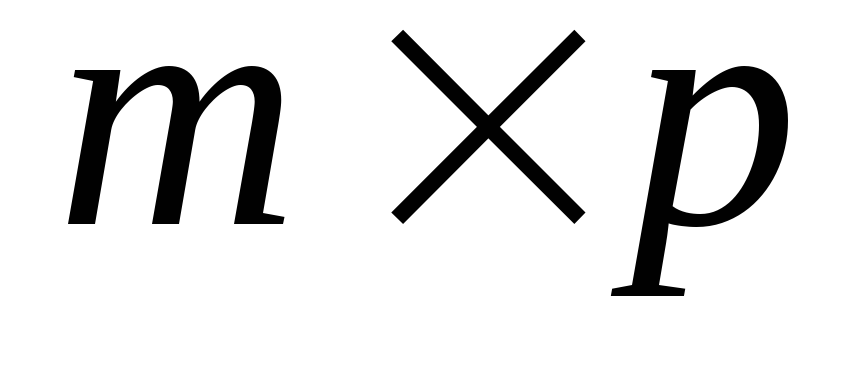 на матрицю
на матрицю розміру
розміру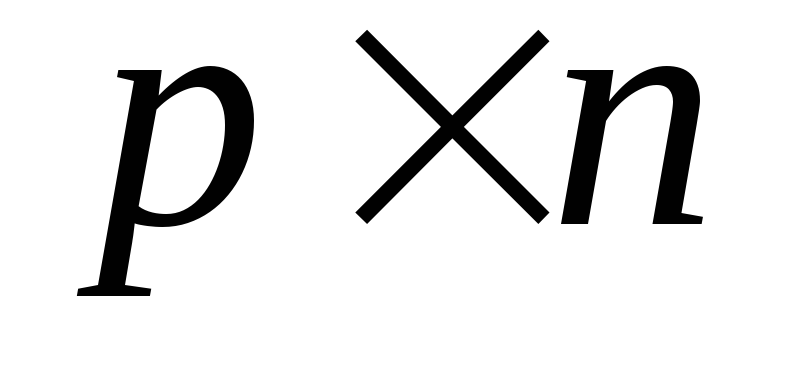 називається така матриця
називається така матриця розміру
розміру
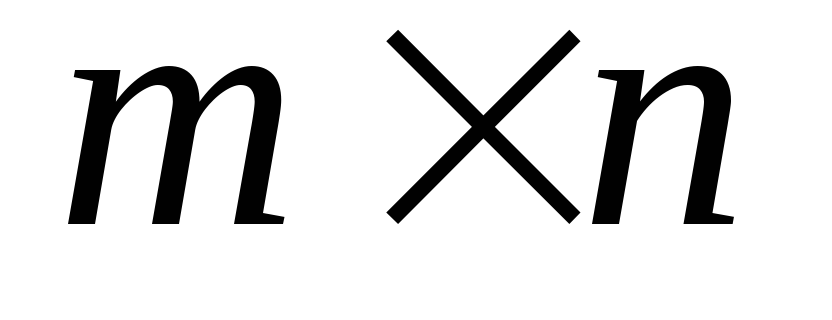 ,
,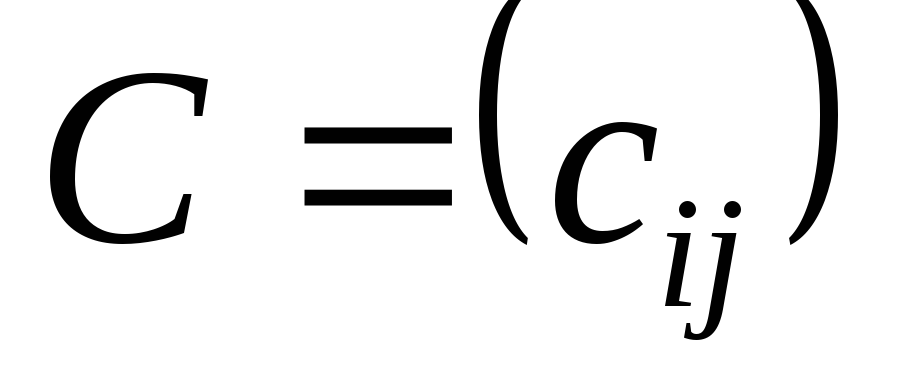 ,
кожний елемент можна знайти за формулою:
,
кожний елемент можна знайти за формулою:
![]() .
.
Добуток матриць має такі властивості:
А(ВС)=(АВ)С
А(В+С)=АВ+АС
(А+В)С=АС+ВС
к(АВ)=(кА)В
АО=ОА=0

Визначники квадратних матриць. Способи обчислення визначників
Квадратній матриці А п-го порядку можна поставити у відповідність число detA, яке називаюь визначником цієї матриці.
При n=1
detA=![]()
при
n=2
detA=![]()
при n=3
часто користуються правилом трикутника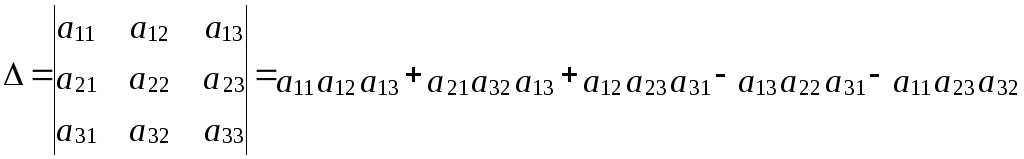 ,
,
чи методом Саррюса (додають до матриці ще два перших стовпчика (вниз – плюс, вверх – мінус))
Визначник n-го порядку. Теорема Лапласа
Визначником n–ого порядку називається число, яке дорівнює алгебраїчній сумі добутків елементів будь-якого рядка, або стовпчика на відповідні їм алгебраїчні доповнення.
Т. Лапласа: визначник дорівнює сумі добутків усіх елементів будь-якого рядка на їх алгебраїчне доповнення
Визначники. Властивості визначників
Квадратній матриці А п-го порядку можна поставити у відповідність число detA, яке називаюь визначником цієї матриці.
Властивоті визначника:
1. Визначник не змінюється в результаті транспонування.
З властивості 1 випливає, що будь-яке твердження, котре справджується для рядків визначника, справджується і для його стовпців, і навпаки.
2. Якщо один із рядків визначника складається лише з нулів, то такий визначник дорівнює нулю.
3. Якщо поміняти місцями будь-які два рядки визначника, то його знак зміниться на протилежний.
4. Визначник, який має два однакові рядки, дорівнює нулю.
5. Якщо елементи будь-якого рядка визначника помножити на стале число С, то й визначник помножиться на С.
З останньої властивості випливає, що спільний множник елементів рядка можна виносити за знак визначника.
6. Визначник, який має два пропорційні рядки, дорівнює нулю.
7. Якщо всі елементи будь-якого рядка визначника можна подати у вигляді суми двох доданків, то такий визначник дорівнює сумі двох визначників, у яких елементами цього рядка будуть відповідно перший доданок у першому визначнику і другий доданок у другому визначнику, а решта елементів будуть ті самі, що й у початковому визначнику.
8. Визначник не зміниться, якщо до елементів будь-якого рядка додати відповідні елементи довільного іншого рядка, попередньо помножені не деяке число.
Мінори та алгебраїчні доповнення
Мінором
![]() елемента
елемента![]() визначниа
n-го порядку називається визначник
(n-1)-го порядку, який одержимо з даного
визначника шляхом викреслювання i-го
рядка та j-го стовпчика, на перетині яких
знаходиться елемент
визначниа
n-го порядку називається визначник
(n-1)-го порядку, який одержимо з даного
визначника шляхом викреслювання i-го
рядка та j-го стовпчика, на перетині яких
знаходиться елемент![]()
Алгебраїчним
доповненням
![]() елемента
елемента![]() визначника називають мінор цього
елемента, взятий із знаком плюс, якшо
сума рядків і стовпчиків число парне,
та зі знаком мінус, коли непарне, тобто:
визначника називають мінор цього
елемента, взятий із знаком плюс, якшо
сума рядків і стовпчиків число парне,
та зі знаком мінус, коли непарне, тобто:![]()
Обернена матриця. Алгоритм оберненої матриці
Матриця
А–1
називається оберненою
матрицею до квадратної неособливої
матриці
А,
якщо виконується співвідношення:
![]() .
.
Знаходять обернену матрицю таким чином:
1.
![]()
2. Алгебрарічні
доповнення
![]() ,
до всіх елементів матриціА.
,
до всіх елементів матриціА.
3. З
алгебра річних доповнень складають
матрицю в яку записують алгебраїчні
доповнення не в звичайному порядку, а
в транспоновану -
![]()

4.
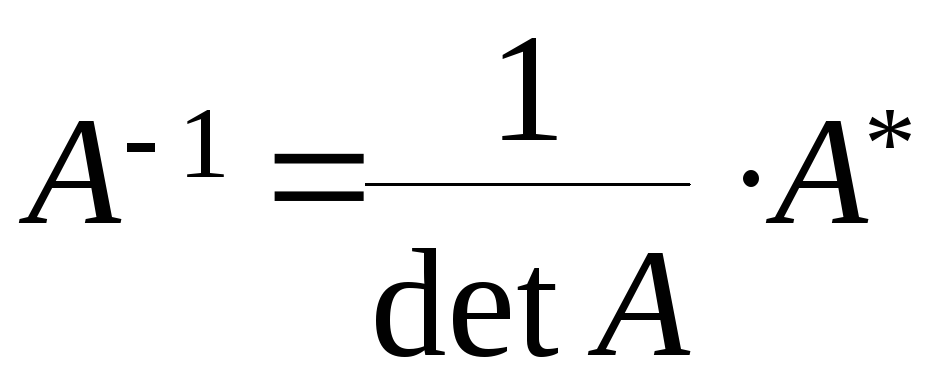
Ранг матриці. Властивості рангу матриці
Рангом
матриці
А
розміром
![]() називається найвищий порядок відмінного
від нуля мінора, утвореного з елементів
цієї матриці , при цьому мінор не дорівнює
0. Позначають r, rangA чи r(A).
Мінор, порядок якого визначає ранг
матриці називається базисним.
називається найвищий порядок відмінного
від нуля мінора, утвореного з елементів
цієї матриці , при цьому мінор не дорівнює
0. Позначають r, rangA чи r(A).
Мінор, порядок якого визначає ранг
матриці називається базисним.
Властивості рангу матриці:
Ранг матриці дорівнює 0 тільки тоді, коли матриця нульова.
Ранг прямокутної матриці не перевищує меншого із її розмірів m чи n, тобто
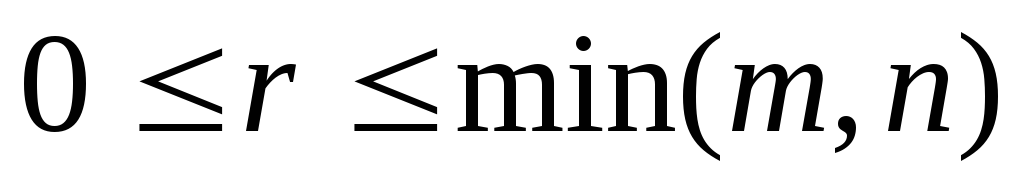
Для квадратної матриці n-го порядку r=n тільки тоді, коли матриця неособлива
Якщо r<n, то визначник даної квадратичної матриці дорівнює нулю.
Основні поняття системи n лінійних алгебраїчних рівнянь з n змінними
 (1.1)
(1.1)
Система
(1.1) називається системою
m лінійних рівнянь з
n невідомими
(змінними),
де x1,
x2,
...,
xn
—
невідомі; aij
![]() — коефіцієнти системи рівнянь; bi
— коефіцієнти системи рівнянь; bi
![]() — вільні члени, або праві частини системи
рівнянь. Якщо всі
bi
=
0
— вільні члени, або праві частини системи
рівнянь. Якщо всі
bi
=
0
![]() ,
то система лінійних рівнянь називається
однорідною.
,
то система лінійних рівнянь називається
однорідною.
Розв’язком системи рівнянь (1.1) є множина таких чисел k1, k2, ..., kn, у результаті підставляння яких замість від- повідних невідомих x1, x2, ..., xn у кожне з рівнянь систе- ми (1.1) останні перетворюються на правильні числові рів- ності.
Якщо система рівнянь не має жодного розв’язку, вона називається несумісною, а якщо має хоча б один розв’язок — сумісною. Сумісна система рівнянь називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо розв’язків більш як один.
Матричний метод розв`язання СЛАР. Алгоритм розв`язування системи матричним способом
Запишемо
систему в матричній формі і знайдемо
її розв`язок. А*Х=В домножимо зліва на![]() ,
маємо
,
маємо![]() *А*Х=
*А*Х=![]() *В.
Оскільки
*В.
Оскільки![]() *А=Е
і Е*Х=Х, то отримуємо Х=
*А=Е
і Е*Х=Х, то отримуємо Х=![]() *В
*В
Алгоритм розв`язання матричним способом:
Перевіряємо виконання умов:
система повинна бути неоднорідною,
кількість рівнянь повинна дорівнювати кількості невідомих,
визначник основної матриці не дорівнює нулю
Знайти матрицю
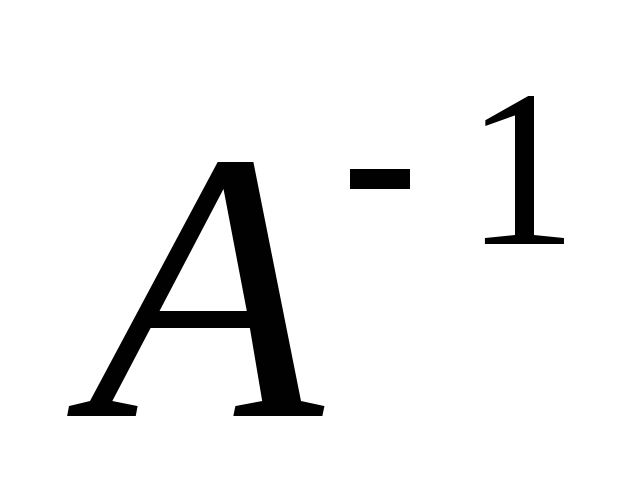 ,
обернену до основної матриці А
,
обернену до основної матриці АЗнайти розв`язок Х шляхом множення матриці
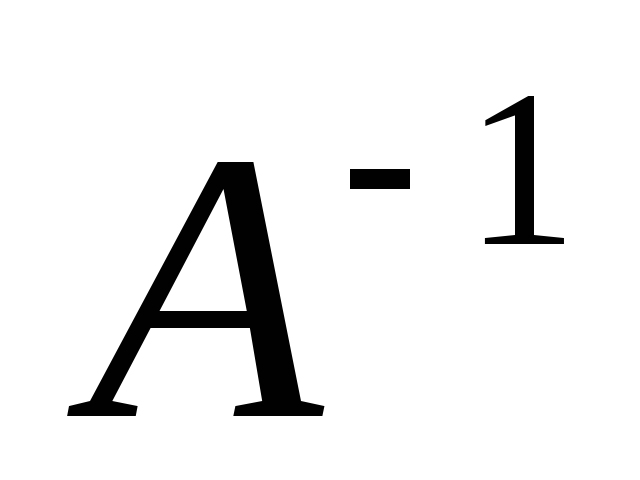 на матрицю вільних членів В, тобто Х=
на матрицю вільних членів В, тобто Х=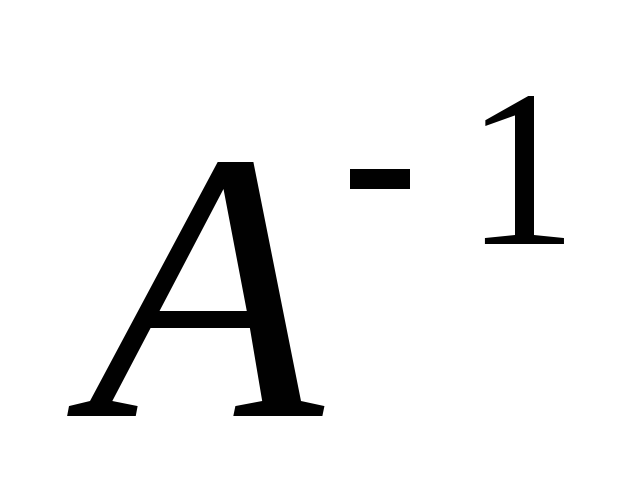 *В
*В
Теорема Кронекера-Капеллі. Алгоритм розв`язування СЛАР
Теорема
Кронекера—Капеллі.
Для того щоб система рівнянь (1.1) була
сумісною (мала розв’язок), необхідно і
достатньо, щоб ранг основної матриці А
дорівнював рангу розширеної матриці
![]() :
:
![]()
З теореми випливає, що в матриці, складеної з коефіцієнтів при невідомих, неодмінно існує мінор r-го порядку, відмінний від нуля, оскільки ранг цієї матриці дорівнює r.
Алгоритм розв`язання СЛАР:
Знайти ранг основної і розширеної матриць системи. Якщо
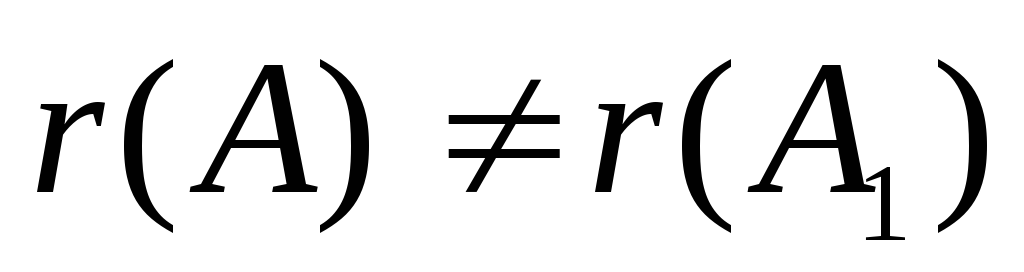 ,
то система несумісна, і розв`язування
СЛАР припиняється
,
то система несумісна, і розв`язування
СЛАР припиняєтьсяЯкщо
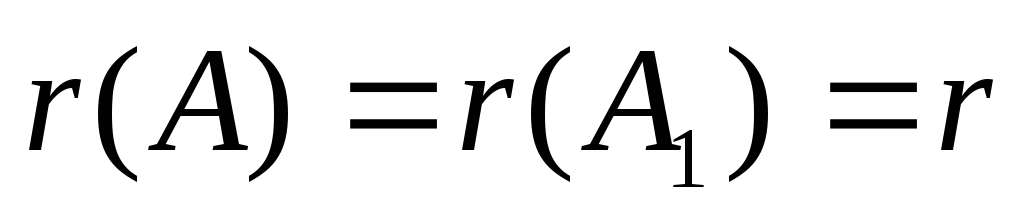 ,
то потрібно взяти r рівнянь, із коефіцієнтів
яких складається базисний мінор, інші
рівняння відкинути
,
то потрібно взяти r рівнянь, із коефіцієнтів
яких складається базисний мінор, інші
рівняння відкинутиНевідомі, коефіцієнти яких входять у базисний мінор, називаються базисними, їх залишають зліва, а інші (n-r) невідомі називаються вільними і їх переносять у праву частину рівняння
Виразити базисні невідомі через вільні
Якщо надати вільним змінним значення нуль, то такий розв`язок називають базисним. Невід`ємний базисний розв`язок називають опорним.
Основні поняття системи m лінійних рівнянь з n змінними. Розв`язок СЛАР методом Гаусса
Метод Жордана-Гауса. Алгоритм кроку перетворення Жордана-Гаусса
Щоб не виконувати обернений хід метола Гаусса, здійснюють повне виключення невідомих у стовпчику за допомогою розв`язувального елемента. Цей модифікований метод Гаусса називають методом Жордана-Гаусса.
Алгоритм кроку перетворення ЖорданаГаусса:
Обираємо розв`язу вальний елемент
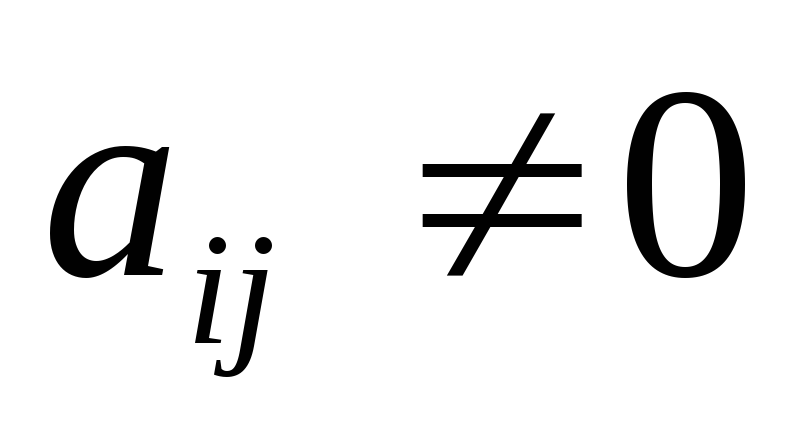 ,
найкраще взяти одиницю.
,
найкраще взяти одиницю.Елементи і-го рядка ділимо на
 і записуємо в і-тий рядок
і записуємо в і-тий рядокУ розв`язу вальному j-тому стовпці замість
 пишуть одиницю, а замість інших елементів
цього стовпця пишуть 0.
пишуть одиницю, а замість інших елементів
цього стовпця пишуть 0.Усі інші елементи знаходять за формулою:
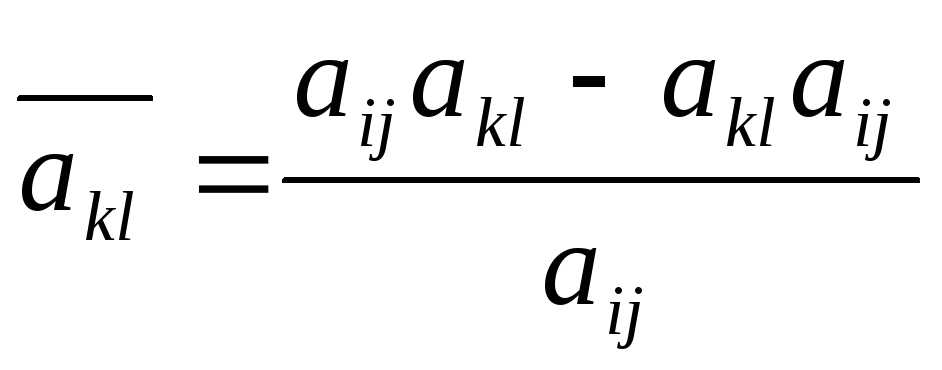
Основні поняття СЛАР. Системи лінійних однорідних рівнянь
Скалярний і векторний добуток. Властивості векторного добутку
Скалярним
добутком двох ненульових векторів
![]() і
і
![]() називається число (скаляр), яке дорівнює
добутку модулів цих векторів на косинус
кута між ними. Якщо хоча б один із векторів
дорівнює нулю, то кут між векторами не
визначений і за означенням скалярний
добуток дорівнює нулю.
називається число (скаляр), яке дорівнює
добутку модулів цих векторів на косинус
кута між ними. Якщо хоча б один із векторів
дорівнює нулю, то кут між векторами не
визначений і за означенням скалярний
добуток дорівнює нулю.
Отже:
![]() ,
,
де — кут між векторами. Використовуючи формулу проекції вектора, можна також записати:
![]() .
.
Векторним
добутком векторів
![]() і
і![]() називається третій вектор
називається третій вектор![]() :
:
довжина вектора с дорівнює
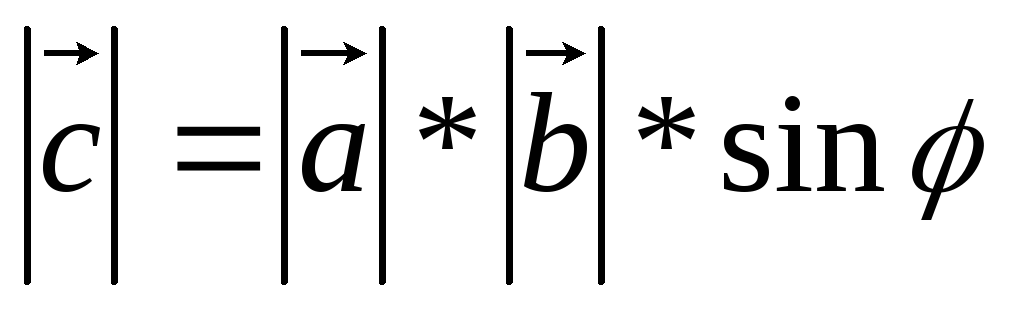 ,
де
,
де - кут між векторами a i b
- кут між векторами a i bвектор с перпендикулярний до кожного з векторів а і b
вектори а b c утворюють праву трійку векторів
Властивості векторного добутку:
a*b=-b*a (антикомунікативність)
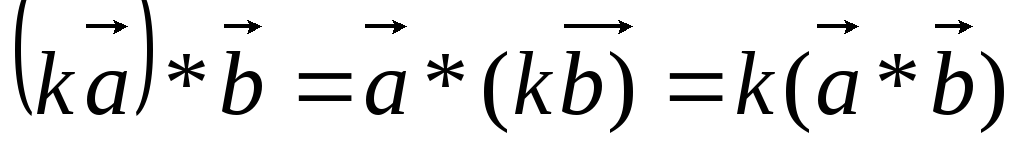 ,
де k=const
,
де k=consta*(b+c)=a*b+a*c (роз подільність)
a*b=0, коли a=0 або b=0, або
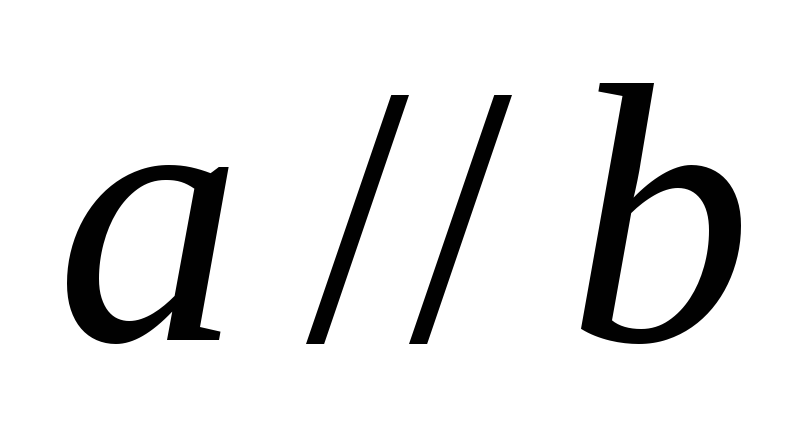
Модуль вектора c=a*b дорівнює площі паралелограма, побудованого на векторах a i b
Векторний добуток векторів
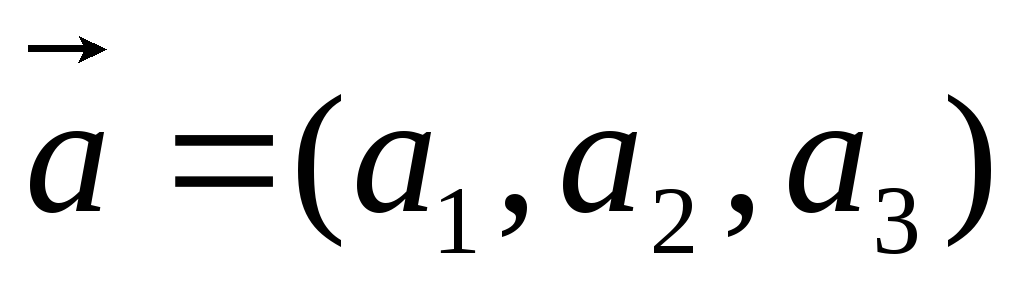 та
та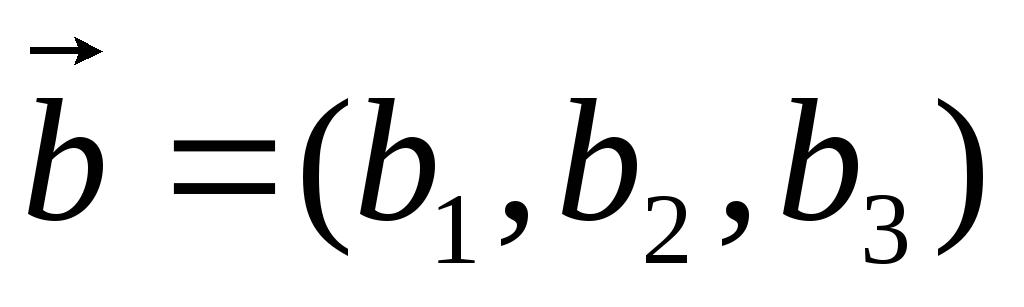 визначається формулою
визначається формулою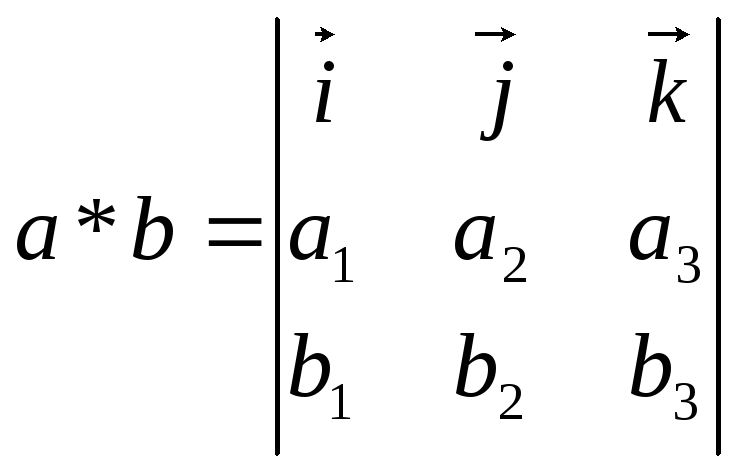
Мішаний добуток, властивості мішаного
Векторний простір, його розмірність і базис. Розклад вектора за базисом. Лінійно залежні і лінійно незалежні системи векторів
Упорядкована
множина n дійсних чисел
![]() називається n-вимірним просторомRn
називається n-вимірним просторомRn
Максимальне число лінійно незалежних векторів простору називається його розмірністю. Розмірність простору дорівнює кількості базисних векторів цього простору.
Базисом n-вимірноговекторного простору Rn називається будь-яка сукупність n лінійно незалежних векторів, через які лінійно виражається довільний вектор цього простору.
Якщо вектори а1, а2,…,аn утворюють базис у просторі Rn, то довільний вектор а цього простору є лінійною комбінацією базисних векторів, тобто існують такі числа х1, х2,…хn, які одночасно не дорівнюють 0, що виконується рівність: а=х1а1+х2а2+…+хnan. Цей вираз називається розкладом вектора за базисом
Для з`ясування питання про лінійну залежність векторів достатньо обчислити ранг матриці, складену з цих векторів:
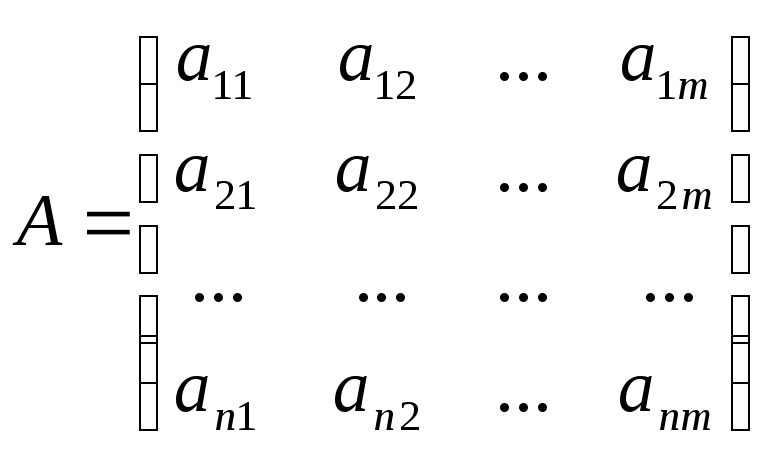
Якщо r(A)=m, то вектори лінійно незалежні, якщо r(A)<m, то вектори лінійно залежні
Рівняння лінії на площині. Вивести канонічне та параметричне рівняння прямої
Вивести рівняння прямої, що проходить через дві точки і рівняння прямої у відрізках на осях.
Відомі
координати двох точок на прямій L:
M1(x1;y1) та M2(x2;y2).
Складаємо
рівняння прямої L. Вектор M1M2 належить
прямій L, отже це напрямний вектор прямої
L. Якщо у
канонічне рівняння прямої замість
координат точки Мо(хо:уо)
підставити координати точки M1(x1;y1), а
замість координат напрямного вектора
l(m;k) підставити координати іншого
напрямного вектора прямої – вектора
М1М2, то одержимо рівняння прямої за
двома точками:![]()
Відомо,
що пряма L відсікає на осях координат
відрізки а і b. Складемо рівняння цієї
прямої. Точки перетину прямої L з осями
координат: М1(а;0), М2(0;b). Використаємо
рівняння прямої за двома точками і
одержимо:
![]() ,
,![]() ,
,![]() ,
,![]() - рівняння прямої у відрізках на осях,
де а – довжига відрізка а осі Ох, b – на
осі Оу.
- рівняння прямої у відрізках на осях,
де а – довжига відрізка а осі Ох, b – на
осі Оу.
Вивести векторне рівняння прямої та загальне рівняння прямої і його частинні випадки
У прямокутній сис-мі координат пряма лінія задається р-ням першого степеня відносно х і у. Загальне р-ня прямої лінії
Ax+By+C=0. Дослідимо це р-ня.
1. С=0, А≠0, В≠0, Ах+Ву=0, визначається як пряма, що проходить через початок координат.
2. В=0, А≠0, С≠0, тоді Ах+С=0, або
![]() ,
де а- довжина відрізка, що його пряма
відтинає на осі Ох, а сама вона розміщена
паралельно осі Оу.
,
де а- довжина відрізка, що його пряма
відтинає на осі Ох, а сама вона розміщена
паралельно осі Оу.
3. А=0, В≠0, С≠0, тоді Ву+С=0, або
![]() ,
де b-
довжина відрізка, що відтинає пряма на
осі Ох.
,
де b-
довжина відрізка, що відтинає пряма на
осі Ох.
Вивести нормальне рівняння прямої та рівняння пучка прямих
Нехай відома відстань р від точки О(0;0) до прямої L, відомо кут а між вектором нормалі і додатним напрямом осі Ох. Потрібно скласти рівняння прямої L.
Координати вектора нормалі ОР знайдемо як проекції його на осі координат:
![]() ,
,
![]() ,
де а – кут між вектором ОР і віссю Ох
,
де а – кут між вектором ОР і віссю Ох
Точка Р
прямої L має такі є самі координати, що
й вектор ОР, тобто
![]()
Складемо
рівняння прямої L за точкою
![]() і
перпендикулярним вектором р(рсоsa;psina)
і
перпендикулярним вектором р(рсоsa;psina)
pcosa(x-pcosa)+psina(y-psina)=0. звідки одержимо нормальне рівняння прямої на площині: хсоsa+ysina-p=0, де р – довжина перпендикуляра, опущеного на пряму з початку координат, а – кут між перпендикуляром і додатнім напрямом осі Ох.
Відомі координати деякої точки Мо(хо;уо) прямої L та кут нахилу а її до осі Ох.
Скористаємося
рівнянням прямої з кутовим коефіцієнтом
у=кх+b. Підставляючи в нього координати
точки Мо і кут
![]() знайдемо значення b=y0-kx0.Шукане
рівняння
прямої набуває вигляду у-у0=k(x-x0).
Якщо
k- змінна величина, то це рівняння описує
пучок
прямих, які проходять через точку Мо.
знайдемо значення b=y0-kx0.Шукане
рівняння
прямої набуває вигляду у-у0=k(x-x0).
Якщо
k- змінна величина, то це рівняння описує
пучок
прямих, які проходять через точку Мо.
Кут між двома прямими заданими канонічними рівняннями. Умови паралельності і перпендикулярності прямих
Рівняння прямої з кутовим коефіцієнтом. Відстань від точки до прямої
Точка
В(0;b) і кут
![]() однозначно визначають пряму L на площині.
Дійсно, адже у=MC+CN=BctgB+b=xtgB+b/
Позначимо k=tgB
і одержимо шукане рівняння прямої з
кутовим коефіцієнтом.
однозначно визначають пряму L на площині.
Дійсно, адже у=MC+CN=BctgB+b=xtgB+b/
Позначимо k=tgB
і одержимо шукане рівняння прямої з
кутовим коефіцієнтом.
Нехай задано деяку точку М0 (х0, у0) і пряму l: Ах + Ву + С = 0. Пересвідчимось, що М0 не лежить на прямій, Ах0 + Ву0 + С 0, тоді відстань від точки М0 (х0, у0) до прямої Ах + Ву + С = 0 можна знайти за формулою:
![]() .
.
Кут між прямими, що задані з кутовим коефіцієнтом. Умови паралельності і перпендикулярності прямих
Розглянемо дві прямі l1: у = k1x + b1 і l2: y = k2 x + b2.
Означення. Кутом між прямим l1 і l2 називається такий кут , поворот на який від першої прямої до другої відносно точки їх перетину до суміщення цих прямих відбувається на найменший кут проти годинникової стрілки.
Рис. 2.15
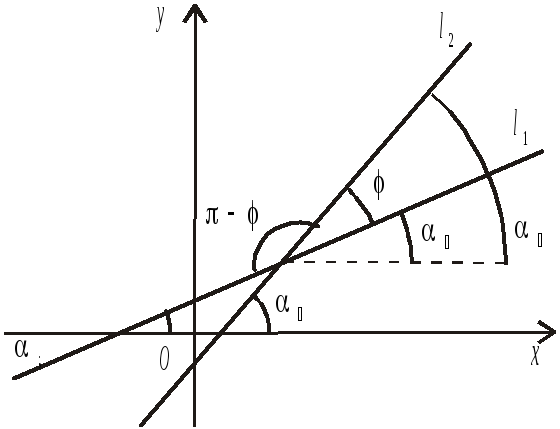
![]()
![]() .
Остаточно
.
Остаточно
![]() .
(2.18)
.
(2.18)
Якщо кут — це кут між l1 і l2, то кут між l2 і l1 дорівнюватиме – .
З формули (2.18) легко дістати умови паралельності і перпендикулярності двох прямих.
Так, коли l1 // l2, кут між ними дорівнює нулю — маємо:
tg = 0 k1 = k2.
Якщо l1
l2,
![]()
![]() .
.
Підставляючи значення кутових коефіцієнтів, маємо:
![]() .
.
Різновиди рівняння площини у просторі: за трьома точками, у відрізках на осях, нормальне.
За трьома точками:
Нехай задано три точки М1(x1;y1;z1), M2(x2;y2;z2), M3(x3;y3;z3), а М(x;y;z) – деяка змінна точка площини. Ветори М1М=(x-x1;y-y1;z-z1) М1М2(x2-x1;y2-y1;z2-z1) I M1M3=(x3-x1;y3-y1;z3-z1) лежать у шуканій площині, тобто компланарні, тому мішаний добуток цих векторів дорівнює нулю (М1М*М1М2)*М1М3=0
Перепишемо цю рівність у координатній формі і одержимо рівняння площини за трьома точками:
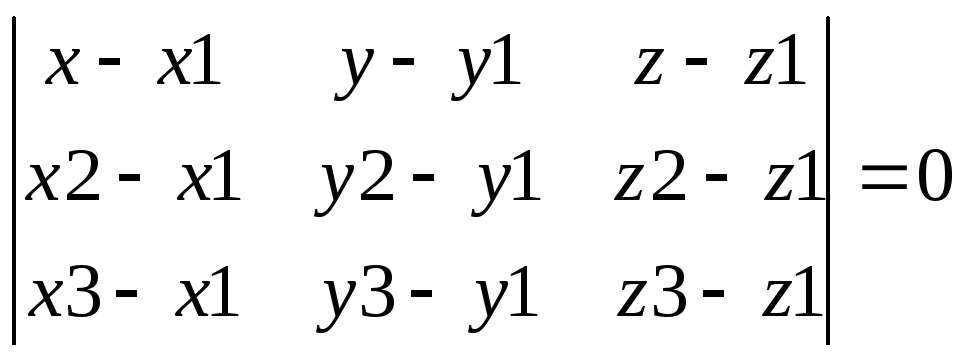
Нормальне рівняння площини у просторі виводиться аналогічно нормальному рівнянню прямої на площині і має вигляд:
Хсоsa+ycosB+zcosj-p=0,
де cosa,
cosB,
cosj
– напрямні косинуси вектора нормалі,
р – довжина вектора нормалі,
![]()
Рівняння
площини у відрізках на осях має вигляд:
![]() ,
де a, b, c – відрізки, які відсікає площина
відповідно на осях Ох, Оу, Оz
,
де a, b, c – відрізки, які відсікає площина
відповідно на осях Ох, Оу, Оz
Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора. Загальне рівняння площини і його дослідження
Кут між площинами. Умови паралельності і перпендикулярності двох площин. Відстань від точки до площини
![]() ,
,
![]() .
.
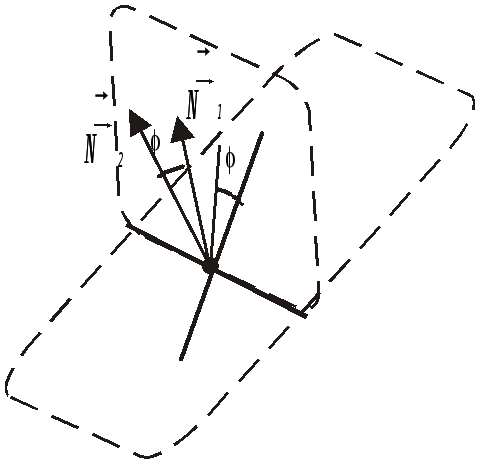
Двогранний кут
між площинами
і
дорівнюватиме ку-
ту між векторами
![]() і
і![]() ,
перпендикулярними до цих площин (рис.
2.21), тому
,
перпендикулярними до цих площин (рис.
2.21), тому
![]() . (2.28)
. (2.28)
Якщо площини взаємно
перпендикулярні, то
![]() і, розкривши скалярний добуток у формулі
(2.28), дістанемо умову перпендикулярності
двох площин:
і, розкривши скалярний добуток у формулі
(2.28), дістанемо умову перпендикулярності
двох площин:
![]() . (2.29)
. (2.29)
Якщо
площини
і
паралельні між собою, то їхні вектори
![]() і
і
![]() — колінеарні,
а отже, відповідні координати пропорційні,
і ми маємо умову
паралельності двох площин
— колінеарні,
а отже, відповідні координати пропорційні,
і ми маємо умову
паралельності двох площин
![]() . (2.30)
. (2.30)
За аналогією з
формулою знаходження відстані від точки
до прямої на площині можна записати
формулу знаходження відстані від точки
![]() до площини
до площини![]() .
Вона набирає вигляду
.
Вона набирає вигляду
![]() .
.
Різновиди рівняння прямої в просторі: канонічне, параметричні, за двома точками. Пряма як перетин двох площин
Кут між прямими в просторі. Кут між прямою і площиною. Умови паралельності і перпендикулярності прямої і площини. Знаходження точки перетину прямої і площини
Кут між
двома прямими L1 i L2 визначається кутом
фі між напрямними векторами
![]() цих прямих, а саме:
цих прямих, а саме:
![]()
Умови паралельності та перпендикулярності двох прямих у просторі випливають з умов паралельності та перпендикулярності їх напрямних векторів:
![]()
![]()
Нехай
пряма L задана канонічним рівнянням
![]() ,
а площина
,
а площина![]() задана загальним рівнянням
Ax+By+Cz+D=0.
Нехай
задана загальним рівнянням
Ax+By+Cz+D=0.
Нехай
![]() - кут між нормальними векторами n=(A,B,C) і
напрямним вектором прямої l=(m;k;p).
Отримуємо:
- кут між нормальними векторами n=(A,B,C) і
напрямним вектором прямої l=(m;k;p).
Отримуємо:
![]() -
формула кута між прямою і площиною
-
формула кута між прямою і площиною
Умови паралельності і перпендикулярності прямої і площини:
![]()
![]()
Для
відшукання точки перетину прямої
![]() і площини Ax+By+Cz+D=0 треба розв`язати систему
рівнянь
і площини Ax+By+Cz+D=0 треба розв`язати систему
рівнянь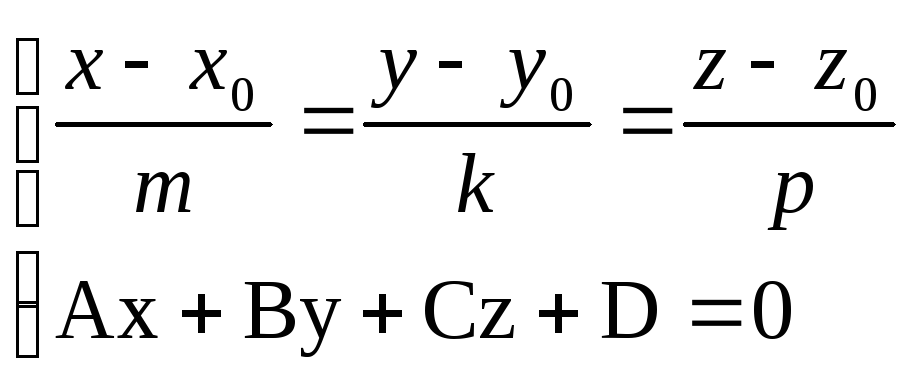 ,
для чого перейдем від канонічного
рівняння прямої до її параметричного
рівняння
,
для чого перейдем від канонічного
рівняння прямої до її параметричного
рівняння![]() ,
,![]() ,
z=zo+pt. Підставивши їх у загальне рівняння
площини, знайдемо значення параметра
t=to. Отримане значення to підставляжмо у
параметричне рівняння прямої і знаходимо
шукану точку М(хо;уо;zo)
,
z=zo+pt. Підставивши їх у загальне рівняння
площини, знайдемо значення параметра
t=to. Отримане значення to підставляжмо у
параметричне рівняння прямої і знаходимо
шукану точку М(хо;уо;zo)
Поняття кривих ліній другого порядку. Дослідження рівняння другого порядку. Коло
Еліпс: означення, рівняння, графік, вершини, півосі, фокуси, ексцентриситет, директриси
Еліпс. Означення. Множина точок площини, для яких сума відстаней від двох заданих точок, що називаються фокусами, є величина стала й така, що дорівнює 2а і більша, ніж відстань між фокусами, називається еліпсом.
Рис. 2.16
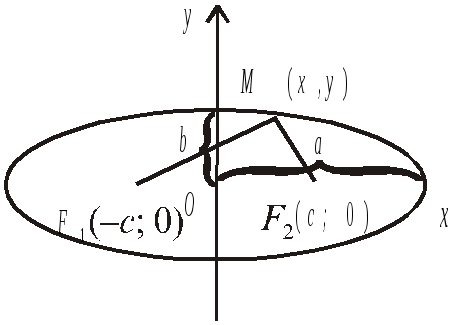
![]() причому 2с
< < 2a
a
> c.
причому 2с
< < 2a
a
> c.
Тоді
![]() (2.20)
(2.20)
канонічне рівняння еліпса, де b2 = а2 – с2.
Розглянемо геометричний зміст параметрів, що входять в рівняння (2.20). Якщо х = 0, у = b, тобто точки (0, b) і (0, – b) є точками перетину еліпса з віссю Оy. Відрізок завдовжки b називають малою піввіссю еліпса. При у = 0, х = а і відповідно (а, 0); (– а; 0) є точками перетину еліпса з віссю Ох. Відрізок завдовжки а — велика піввісь еліпса. З парності виразу (2.20) за х і за у випливає симетрія еліпса відносно осей Ох і Оу. На рис. 2.16 зображено еліпс.
Вершинами еліпса є точки його перетину з осями координат:
з віссю Ох: у=0
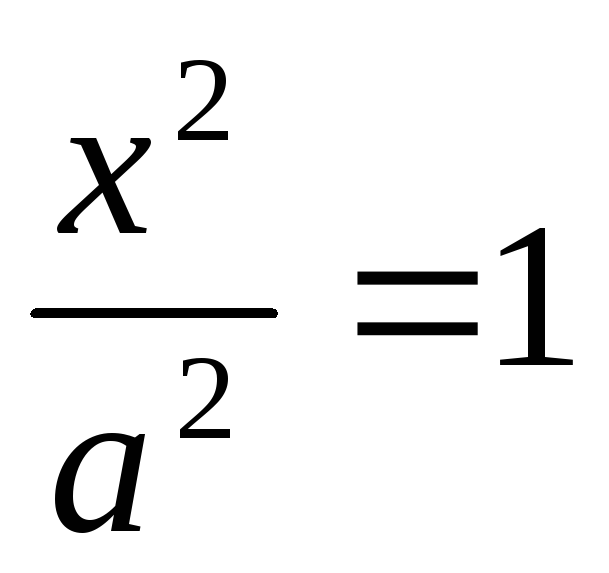 ,
х^2=a^2, x=+-a
,
х^2=a^2, x=+-aз віссю Оу: х=0,
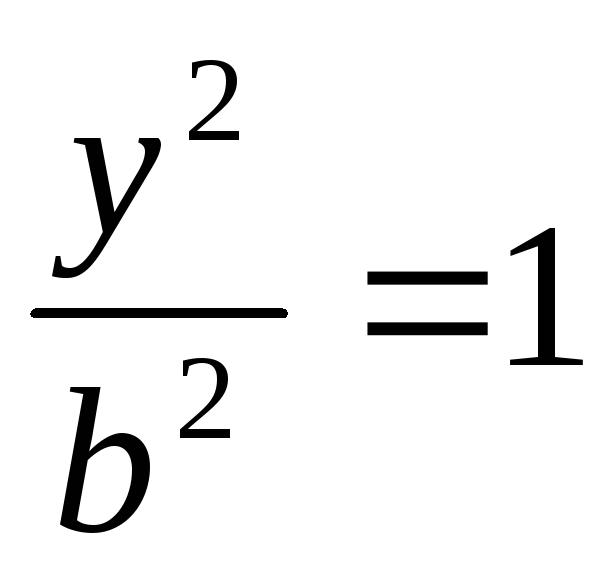 ,
y^2=b^2, y=+-b
,
y^2=b^2, y=+-b
Ексцентриситет
еліпса — це відношення
![]() ;
за означенням
с
<
a
і [0,
1). Оскільки
;
за означенням
с
<
a
і [0,
1). Оскільки
![]() то
то![]() .
З останньої рівності випливає геометричний
зміст ексцентриситету, який полягає в
тому, що він характеризуєступінь
витягнутості
еліпса. Так, при
.
З останньої рівності випливає геометричний
зміст ексцентриситету, який полягає в
тому, що він характеризуєступінь
витягнутості
еліпса. Так, при
![]() маємо коло, якщо
наближається до одиниці, то відношення
довжини півосей еліпса стає малим, тобто
еліпс витягується вздовж осі Ох.
маємо коло, якщо
наближається до одиниці, то відношення
довжини півосей еліпса стає малим, тобто
еліпс витягується вздовж осі Ох.
Дві
прямі, рівняння яких
![]() ,
називаютьсядиректрисами
еліпса.
Для еліпса
,
називаютьсядиректрисами
еліпса.
Для еліпса
![]() і відношення
і відношення![]() ,
директриси еліпса
— це дві прямі, що розміщені симетрично
відносно осі Оу
і проходять зовні еліпса.
,
директриси еліпса
— це дві прямі, що розміщені симетрично
відносно осі Оу
і проходять зовні еліпса.
Гіпербола: означення, рівняння, графік, спряжена гіпербола, вершини, осі, фокуси, ексцентриситет, асимптоти, директриси
Гіперболою наз. множина точок площини, для яких модуль різниці відстаней від двох заданих точок (фокусів), є величина стала, яка дор. 2а і менша за відстань між фокусами.
![]()
Парабола: означення, рівняння, графік, вершина, фокус, ексцентриситет, директриса. Різновиди розміщення параболи на площині та її рівняння.
Означення. Множина точок площини, що містяться на одна- ковій відстані від даної точки фокуса і даної прямої, яка не проходить че- рез фокус і називається директрисою, є парабола.
За означенням r = d, отже
:
![]() або у2
= 2рх
або у2
= 2рх
— канонічне рівняння параболи, коли = 1. Парабола симетрична осі Ох, проходить через початок системи координат. Її графік подано на рис. 2.18.
Точка
О(0;0) – вершина параболи. Фокус - точка,
від якої рівновіддалені сума точок
параболи. Ексцентриситет
параболи = 1.
Дисектриса параболи дорівнює х=![]()
Різновиди парабол: у^2=2px, y^2=-2px, x^2=2py, x^2=-2py
Поняття числової послідовності: формула п-го члена, зростаюча спадна, обмежена послідовність.
Числова функція у=ƒ(n), область виз-ня якої є множина нат. ряду чисел, наз. числ. послідовністю і позн. хn= ƒ(n).
Геометрична інтерпретація границі послідовності. Основні властивості границь послідовності
Розглянемо
геометричну інтерпретацію границі
послідовності. На числовій осі побудуємо
-окіл
числа а,
тобто інтервал (а
– ;
а + ),
і покажемо, як розміщуватимуться точки,
які відповідають членам послідовності
![]() ,
при
,
при![]() (рис. 3.12).
(рис. 3.12).
![]()
Рис. 3.12
![]() ,
усі члени послідовності перебувають в-околі
точки а
(див. рис. 3.12).
,
усі члени послідовності перебувають в-околі
точки а
(див. рис. 3.12).
Загальні властивості збіжних послідовностей
Теорема 1. (Єдиність границі послідовності). Якщо послідовність має границю, то вона єдина.
Теорема 2. (Необхідна умова збіжності послідовності). Якщо послідовність збіжна, то вона обмежена.
Теорема
3.
Якщо
![]() ,
то існує такий номерN,
що при всіх
,
то існує такий номерN,
що при всіх
![]() виконується нерівність
виконується нерівність![]() .
.
Теорема 4.
Границя сталої величини дорівнює сталій,
тобто
![]()
![]()
Границя функції в точці і на нескінченності: означення, геометрична інтерпретація означення, приклади. Односторонні границі функції в точці
Нескінченно малі функції в точці і на нескінченності означення, властивості, геометрична інтерпретація означення, приклади
Послідовність
![]() називаєтьсянескінченно
малою величиною (н. м. в.),
якщо
називаєтьсянескінченно
малою величиною (н. м. в.),
якщо
![]() .
.
Приклад.
![]() — н.м.в., бо
— н.м.в., бо![]() .
.
Властивості нескінченно малих функцій:
Алгебраїчна сума скінченого числа нескінченно малих функцій є нескінченно мала функція
Добуток нескінченно малої функції на сталу величину або на обмежену функцію є нескінченно мала величина
Частка від ділення нескінченно малої функції на функцію, границя якої не дорівнює нулю, є нескінченно мала функція
Нескінченно великі функції в точці і на нескінченності: означення, властивості, геометрична інтерпретація означення, приклади.
Теорема про зв`язок між нескінченно малими і нескінченно великими функціями. Теорема про зв`язок між нескінченно малими функціями та границею функції
Теорема. Зв’язок між н.в.в. і н.м.в.
1. Якщо — н.М.В. І, то обернена до неї послідовністьбуде н.В.В., і навпаки.
2. Якщо yn — н.В.В., то обернена до неї — н.М.В.
Теорема про зв`язок між нескінченно малими функціями та границею функції:
Функція f(x) має границю А в точці х0 тоді і тільки тоді, коли її можна подати у вигляді суми числа А і нескінченно малої функції а(х) при х прямує до х0, тобто f(x)=A+a(x)
Еквіваленті нескінченно малі величини. Ланцюжок еквівалентних нескінченно малих величин (при x--->0 і при x -- > x0). Теорема про застосування еквівалентно нескінченно малих величин при обчисленні границь функцій.
Властивості функцій, які мають границю в точці: єдність границі, граничний перехід у нерівності, границя проміжної функції, обмеженість функції в точці.
Властивості границь функцій: границя сталої, суми, добутку, частки функцій, границя степеневої функції
Розкриття невизначеного вигляду
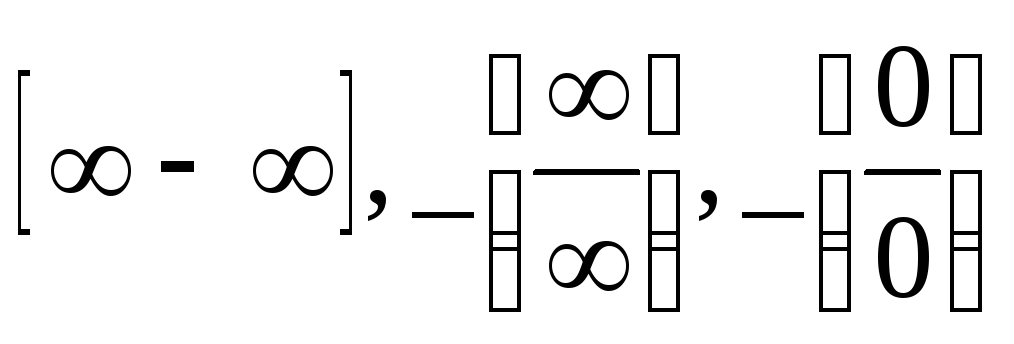 при застосуванні ірраціональних функцій
та многочленів під час обчислення
границь функцій
при застосуванні ірраціональних функцій
та многочленів під час обчислення
границь функцій
Невизначеність
![]() для ірраціональних функцій
для ірраціональних функцій
Для розв’язування задач у цьому випадку рекомендується звільнитись від тих ірраціональних множників у чисельнику і знаменнику дробового виразу, які перетворюються на нуль при виконанні граничного переходу. Для звільнення від радикалів використовують формули скороченого множення, заміну змінної та інші штучні прийоми
Приклад.
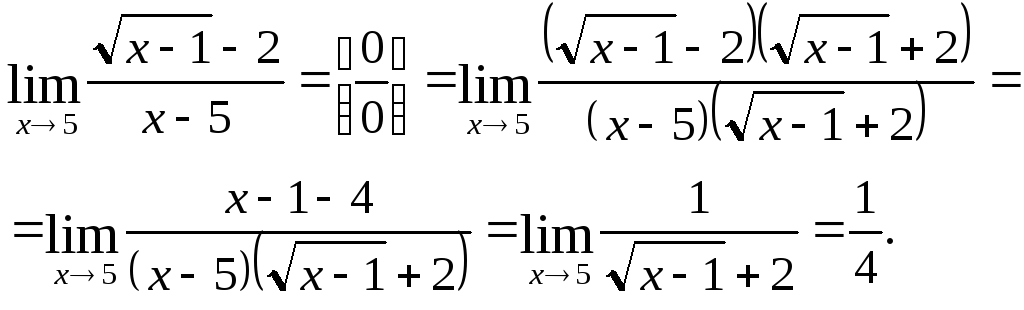
3. Невизначеність
У цьому випадку і чисельник, і знаменник рекомендується поділити на найбільший степінь змінної, що входить як до знаменника, так і до чисельника.
Приклад.
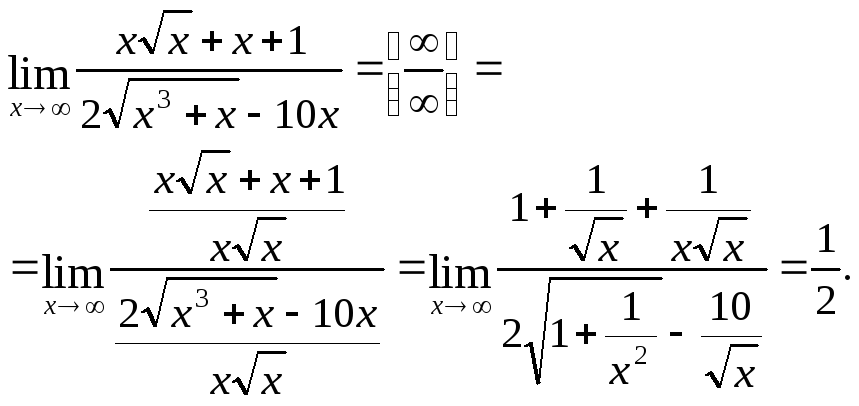
4. Невизначеність
Цей тип
невизначеності зводиться до невизначеностей
![]() або
або![]() наприклад, зведенням виразу до спільного
знаменника, множенням на спряжений
вираз.
наприклад, зведенням виразу до спільного
знаменника, множенням на спряжений
вираз.
Приклад.
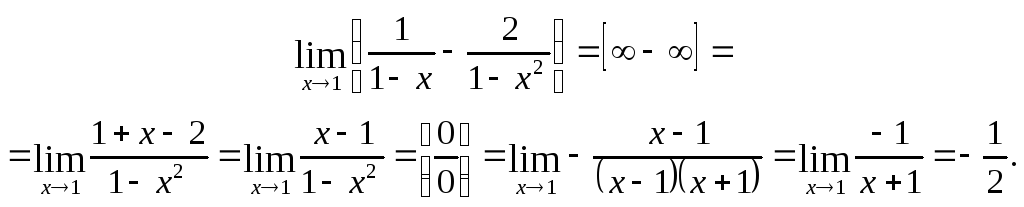
Перша і друга важливі границі та наслідки з них
Перша
особлива границя
![]()
Границі — наслідки першої особливості границі:
1.
![]() 2.
2.![]() 3.
3.![]() 4.
4.![]()
Зауваження.
За допомогою першої особливої границі
можна досліджувати невизначеності
![]() для виразів з тригонометричними
функціями.
для виразів з тригонометричними
функціями.
Друга
особлива границя
![]()
Границі — наслідки другої особливої границі:
1. ![]() . 2.
. 2. ![]() . 3.
. 3.![]() .
.
4. ![]() .
.
Зауваження: За допомогою другої особливої границі та її на- слідків можна досліджувати невизначеності
![]()
Неперервність функції в точці: означення Коші та означення в термінах приростів функції та аргументу. Застосування поняття неперервності при обчисленні границь функцій
Функція
![]() називаєтьсянеперервною
в точці
називаєтьсянеперервною
в точці
![]() якщо
якщо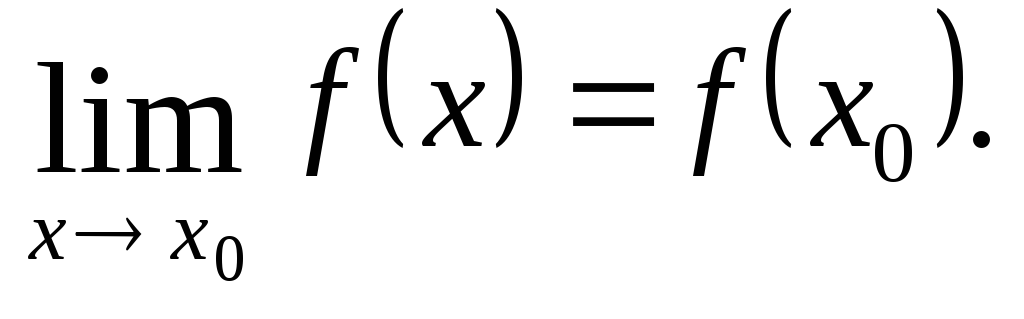
Означення.
Функція
![]() називаєтьсянеперервною
в точці
називаєтьсянеперервною
в точці
![]() якщо в цій точці нескінченно малому
приросту аргументу відповідає нескінченно
малий приріст функції, тобто
якщо в цій точці нескінченно малому
приросту аргументу відповідає нескінченно
малий приріст функції, тобто
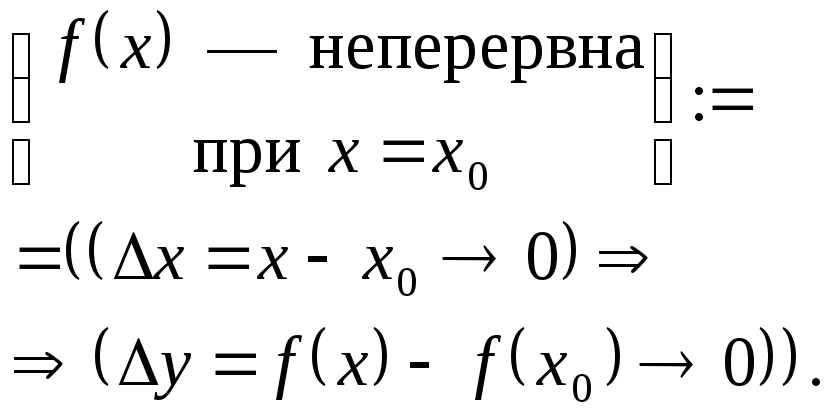
Означення.
Функція
![]() називаєтьсянеперервною
в точці
називаєтьсянеперервною
в точці
![]() якщо границя функції дорівнює функції
від границі аргументу при
якщо границя функції дорівнює функції
від границі аргументу при![]() ,
тобто
,
тобто
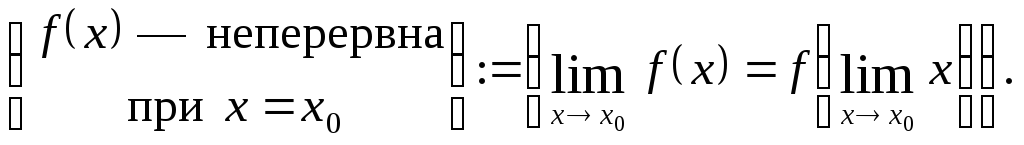
Означення.
Функція
![]() називаєтьсянеперервною
в точці
називаєтьсянеперервною
в точці
![]() якщо односторонні границі функції зліва
й справа в цій точці існують, рівні між
собою і дорівнюють значенню функції у
цій точці, тобто:
якщо односторонні границі функції зліва
й справа в цій точці існують, рівні між
собою і дорівнюють значенню функції у
цій точці, тобто:

Властивості функцій, неперервних у точці. Теорема про неперервність елементарних функцій
Властивості функцій, неперервних на відрізку. Геометрична інтерпретація цих властивостей
Якщо функція y=f(x) неперервна на відрізку [a;b], то вона обмежена на цьому відрізку

Якщо функція y=f(x) неперервна на відрізку [a;b], то вона досягає на цьому відрізку свого найменшого m і найбільшого М значення.

Якщо функція y=f(x) неперервна на відрізку [a;b], і значення її на кінцях відрізках f(a) i f(b) мають протилежні знаки, то в середині відрізка існує хоча б одна така точка,
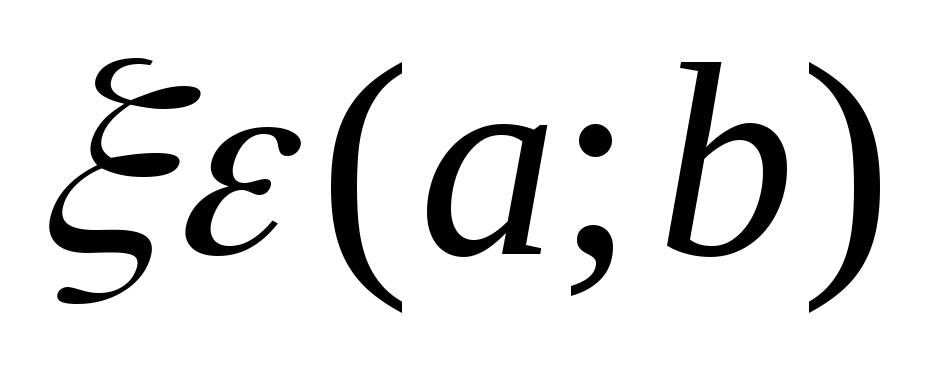 ,
що f(e)=0, тобто криваy=f(x)
перетинає вісь Ох хоча б в одній точці
,
що f(e)=0, тобто криваy=f(x)
перетинає вісь Ох хоча б в одній точці

Точки розриву функції першого роду, другого роду й точки усувного розриву. Геометрична ілюстрація порушення умов неперервності функції у цих точках
Задачі, які призводять до поняття похідної: задача про продуктивність праці, задача про кутовий коефіцієнт дотичної
Означення похідної. Диференційовність та неперервність функції в точці і на проміжку
Правила диференціювання сталої, суми, добутку, частки функцій та наслідки з них
Основні правила диференціювання
Теорема
1.
Похідна сталої дорівнює нулю, тобто
якщо у
= с,
де с
= const, то
![]() .
.
Теорема 2.
Похідна алгебраїчної суми скінченної
кількості диференційовних функцій
дорівнює алгебраїчній сумі похідних
цих функцій:
![]() .
.
Теорема 3. Похідна добутку двох диференційовних функцій дорівнює добутку першого множника на похідну другого плюс добуток другого множника на похідну першого:
![]() .
.
Теорема 4. Сталий множник можна виносити за знак похідної:
![]() ,
де
,
де
![]() .
.
Теорема 5. Якщо
чисельник і знаменник дробу диференційовні
функції (знаменник не перетворюється
в нуль), то
похідна дробу також дорівнює
дробу, чисельник якого є різницею
добутків знаменника на похідну чисельника
і чисельника на похідну знаменника, а
знаменник є квадратом знаменника
початкового дробу
![]() .
.
Зауваження.
Похідну від функції
![]() ,
де
,
де![]() ,
зручно обчислювати як похідну від
добутку сталої величини
,
зручно обчислювати як похідну від
добутку сталої величини![]() на функціюu
(x):
на функціюu
(x):
![]() .
.
Похідна сталої та функції у=х (доведення). Таблиця похідних
Геометричний зміст похідної. Рівняння дотичної. Поняття нормалі до графіка функції та її рівняння. Економічний зміст похідної
