
- •1. Якщо — н.М.В. І, то обернена до неї послідовністьбуде н.В.В., і навпаки.
- •2. Якщо yn — н.В.В., то обернена до неї — н.М.В.
- •3. Невизначеність
- •4. Невизначеність
- •4.1.2. Геометричний зміст похідної
- •2) Якщо в усіх точках проміжку (а, с) друга похідна від’ємна , то графік функції випуклий.
- •1) І, тодіточка максимуму функції;
- •2) І, тодіточка мінімуму функції;
- •3) , Тоді в точцінемає екстремуму.
- •4) , Тоді потрібні додаткові дослідження
1) І, тодіточка максимуму функції;
2) І, тодіточка мінімуму функції;
3) , Тоді в точцінемає екстремуму.
4) , Тоді потрібні додаткові дослідження
Знаходження умовного екстремуму функції кількох змінних
Нехай
на відкритій множині D
R2
задано ф-ії u=f(x;y),
v=(x;y)
і Е
– множина точок, що задовольняють
рівняння:
![]()
Означення:
Рівняння
![]()
![]() називають
рівнянням зв’язку, точку (x0;y0)Е
називають точкою умовного строгого
максимуму ф-ії u=f(x;y)
при обмеженнях рівняння.
називають
рівнянням зв’язку, точку (x0;y0)Е
називають точкою умовного строгого
максимуму ф-ії u=f(x;y)
при обмеженнях рівняння.
Точки умовного максимуму та мінімуму називають точками умовного екстремуму. Умовний екстремум інколи називають відносним екстремумом.
Ф-ція L(x;y)=f(x;y)+(x;y) наз. ф-цією Лагранжа, параметр - множн. Лагнаржа.
Теорема.
Для того, щоб т. (х0;у0) була т. умовного екстр. ф-ції u=f(x;y) при р-ні звязку (х;у)=0, необ., щоб її координ. При деяких знач. задов. сис-му р-нь:

Алгоритм знаходження умовного екстремуму методом Лагранжа
Записати функцію Лагранжа
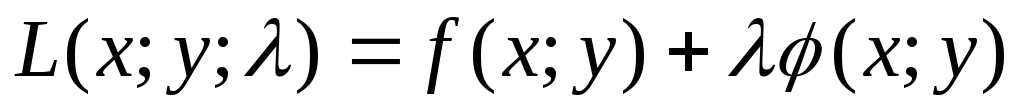 ,
де
,
де -
деяке число, що називається множником
Лагранжа
-
деяке число, що називається множником
ЛагранжаЗнайти критичні точки функції Лагранжа за необхідними умовами існування екстремуму

Перевірити в кожній критичній точці Мk достатні умови існування екстремуму:
А) якщо
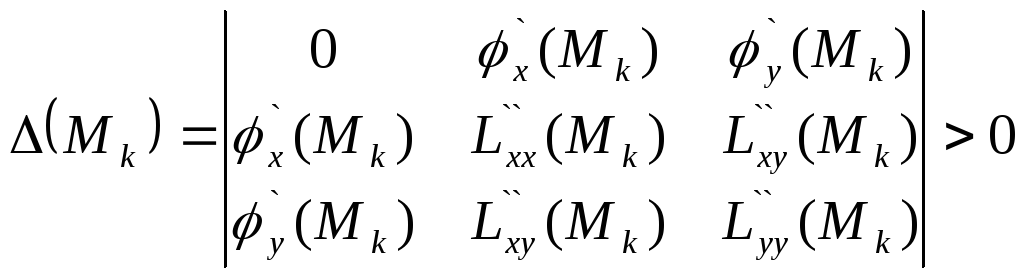 ,
то
,
то
![]() -точка
максимуму
-точка
максимуму
Б) якщо
![]() <0
, то
<0
, то![]() - точка мінімуму
- точка мінімуму
4) Знайти значення функції у точках максимуму чи мінімуму
Знаходження найбільшого та найменшого значення функції в області D
Первісна для заданої функції, її основні властивості
Функція F(x) називається первісною для ф-ії f(x) на проміжку І, якщо на цьому проміжку F`(x)=f(x) або dF(x)=f(x)dx.
Із означення виходить, що первісна F(x) – диференційована, а значить неперервна функція на проміжку І, і її вигляд суттєво залежить від проміжку, на якому вона розглядається.
Будь-які дві первісні для заданої функції відрізняються дише на сталу С
Невизначений інтеграл і його властивості
Функція F(x) + С, що являє собою загальний вигляд всієї множини первісних для функції f(x) на проміжку І, називається невизначеним інтегралом від функції f(x) на проміжку І і позначається
![]() ,
,
![]() ,
(7.1)
,
(7.1)
де
![]() —
знак невизначеного інтеграла;
—
знак невизначеного інтеграла;
f(x) — підінтегральна функція;
f(x)dx — підінтегральний вираз;
Рис. 7.2
Властивості невизначеного інтеграла
І. Похідна від
невизначеного інтеграла дорівнює
підінтегральній функції
![]() .
.
ІІ. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.
ІІІ.
![]() .
.
б) Властивості, що відображають основні правила інтегрування.
IV. Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла, тобто
![]() (7.2)
(7.2)
V. Невизначений
інтеграл від суми функцій дорівнює сумі
невизначених інтегралів від цих функцій,
якщо вони існують, тобто
![]()
Метод безпосереднього інтегрування невизначених інтегралів
Метод безпосереднього інтегрування ґрунтується на використанні таблиці основних інтегралів, властивостей невизначеного інтеграла. Але в деяких випадках спочатку потрібно зробити алгебраїчні перетворення підінтегральної функції
Знаходження невизначених інтегралів методом заміни змінної
Метод підстановки (заміни змінної): f(x)dx=f((t))’(t)dt
Мета методу підстановки — перетворити даний інтеграл до такого вигляду, який простіше інтегрувати.
Теорема 4.
Якщо f(x)
— неперервна, а
![]() має непе-
рервну похідну, то:
має непе-
рервну похідну, то:
 (7.6)
(7.6)
Наслідок.
![]() (7.7)
(7.7)
Зауваження. Специфіка інтегрування невизначеного інтеграла не залежить від того, є змінна інтегрування незалежною змінною чи сама є функцією (на підставі інваріантності форми запису першого диференціалу), тому, наприклад:

Знаходження невизначених інтегралів методом інтегрування частинами
Цей метод
застосовується, якщо під знаком інтеграла
є добуток функцій, причому хоча б одна
з них не є степеневою. Формула інтегрування
частинами має такий вигляд:
![]() .
Ця формула застосовується, коли одержаний
інтеграл
.
Ця формула застосовується, коли одержаний
інтеграл
![]() менш складний, ніж данний
менш складний, ніж данний
![]()
Інтегрування функцій, які містять у знаменнику квадратний тричлен.
Інтегрування виразів з квадратним тричленом.
![]()
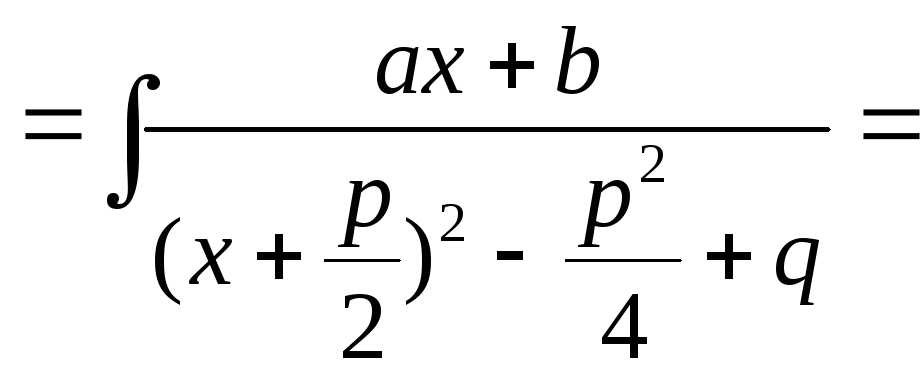



![]()
Інтегрування функцій, які містять у знаменнику квадратний тричлен
Інтегрування виразів з квадратним тричленом.
![]()
а)D>0- розклад. на елемент. дроби
б) D=0- виділення повного кв
в) D<0-
ах2+bх+c=а(х2+![]() +
+![]() )=а(х2+2х
)=а(х2+2х![]() +
+![]() )=
)=
а(![]() )
)
![]() =2.
=2.

Метод невизначених коефіцієнтів
Інтегрування функцій, що містять ірраціональності
При
інтегруванні виразів, що містять
ірраціональності методом підстановки,
зводять підінтегральну функцію до
раціонального дробу. Якщо підінтегральна
функція є раціональним дробом відносно
![]() ,
де а – дробове число, то в цьому випадку
вводять нову змінну
,
де а – дробове число, то в цьому випадку
вводять нову змінну![]() ,
де q – спільний знаменник дробових
показників степеня змінної х.
,
де q – спільний знаменник дробових
показників степеня змінної х.
)

2)![]()
3)
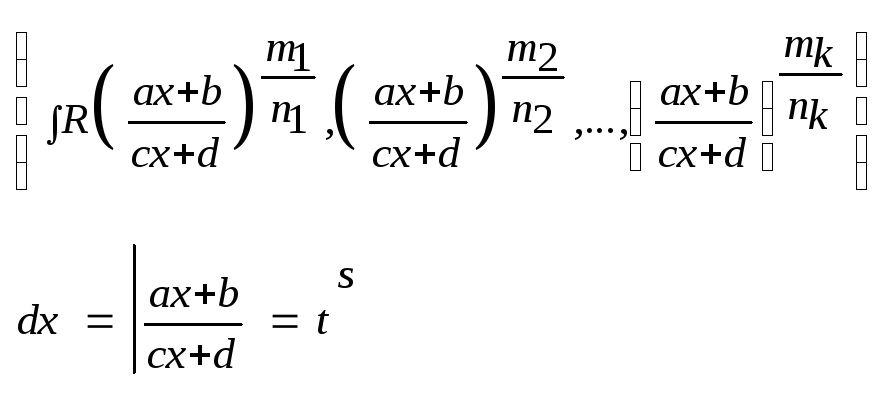
Підінтегральна
ф-ія
![]() після
виділення повного квадрата і заміни
після
виділення повного квадрата і заміни![]() раціоналізується
тригонометричними підстановками.
раціоналізується
тригонометричними підстановками.
Інтегрування тригонометричних функці
Розглянемо R(sin x,cos x)dx, де R – раціональна ф-ія відносно sin, cos, тобто над sin, cos викон. лише арифметичні дії та піднесення до цілого степеня. Існують такі підстановки, що за їх допомогою інтеграл R(sinx,cosx)dx завжди може бути зведений до інтеграла від раціональної ф-ії R*(t)dt, загальна схема інтегрування якої розроблена.
1) Універсальна
тригонометрична підстановка
![]() .
На практиці універсальну тригонометричну
підстановку використовують, якщоsin
x, cos x входять
в невисокому степені, інакшфе
підрахунки будуть складні.
.
На практиці універсальну тригонометричну
підстановку використовують, якщоsin
x, cos x входять
в невисокому степені, інакшфе
підрахунки будуть складні.
2) Підінтегральна ф-ія – непарна відносно sin x, тоді роблять підстановку cos x = t.
3) Підінтегральна ф-ія – непарна відносно cos x раціоналізується за допомогою підстановки sin x = t.
4) Підінтегральна ф-ія R(sin x, cos x) – парна по sinx, cosx сукупно, тобто R(-sinx,-cosx)=R(sinx,cosx). В цьому випадку використовують підстановку tgx=t або ctgx=t.
5) Підінтегральна ф-ія R(tgx) раціоналізується підстановкою tgx=t.
В інтегралах sin2nxcos2mxdx рекомендується скористатися формулами зниження степеня.
Інтегрування найпростіших раціональних дробів
Відношення двох
многочленів![]() називаєтьсяраціональним
дробом.
називаєтьсяраціональним
дробом.
Означення: Раціональний дріб правильний, якщо степінь многочлена в чисельнику менший степеня многочлена в знаменнику, тобто n<m. Якщо ж nm, то дріб неправильний.
Найпростіші раціональні дроби (4 типи):
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]()
де k2, kN, D=p2-4q<0
Теорема: Будь-який правильний раціональний нескоротний дріб можна представити у вигляді скінченого числа найпростіших дробів використовуючи такі правила:
1) Якщо Qm(x)=(x-a)kgm-k(x), то:
![]()
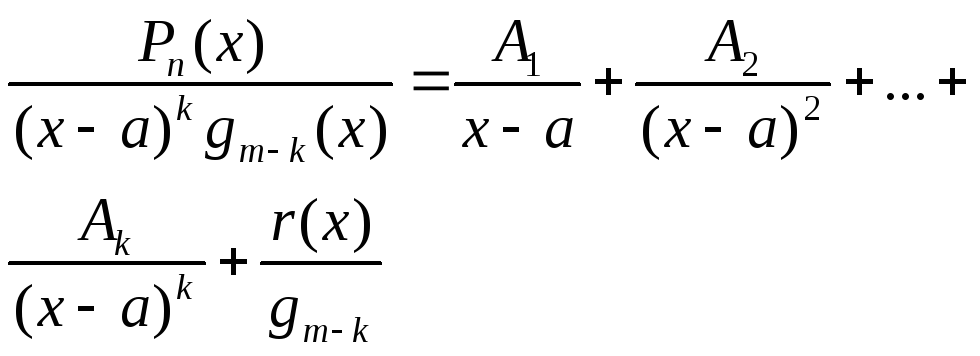
2) Якщо Qm(x)=(x2+px+q)kgm-2k(x), то:

де Аі,
Ві,
![]() –
деякі коефіцієнти,
–
деякі коефіцієнти,![]() та
та![]() правильні
раціональні дроби.
правильні
раціональні дроби.
Методика інтегрування раціональних ф-ій:
1. Якщо підінтегральна ф-ія – неправильний раціональний дріб, то за допомогою ділення його розкладають на суму многочлена і правильного раціонального дробу.
2. Знаменник правильного раціон. дробу розкладають на множники. По вигляду знаменника, правильний раціон. дріб представляють у вигляді найпростіших дробів, використовуючи метод невизначених коефіцієнтів.
3. Інтегрують цілу частину і найпростіші дроби.
Інтегрування найпростіших раціональних дробів
Відношення двох
многочленів![]() називаєтьсяраціональним
дробом.
називаєтьсяраціональним
дробом.
Означення: Раціональний дріб правильний, якщо степінь многочлена в чисельнику менший степеня многочлена в знаменнику, тобто n<m. Якщо ж nm, то дріб неправильний.
Найпростіші раціональні дроби (4 типи):
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]()
де k2, kN, D=p2-4q<0
Теорема: Будь-який правильний раціональний нескоротний дріб можна представити у вигляді скінченого числа найпростіших дробів використовуючи такі правила:
1) Якщо Qm(x)=(x-a)kgm-k(x), то:
![]()
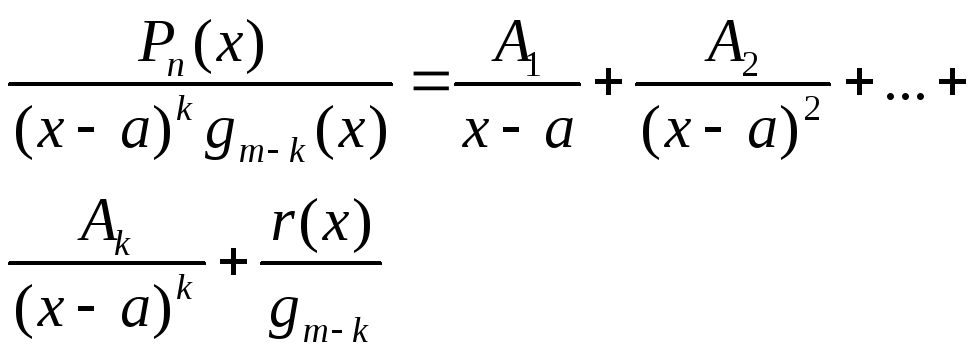
2) Якщо Qm(x)=(x2+px+q)kgm-2k(x), то:
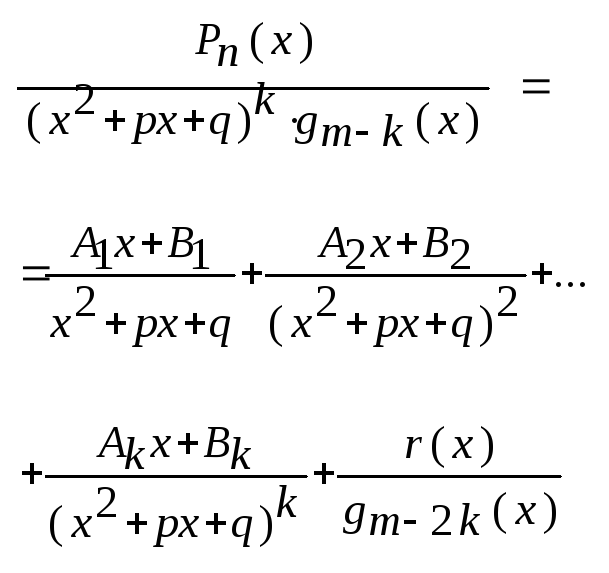
де Аі,
Ві,
![]() –
деякі коефіцієнти,
–
деякі коефіцієнти,![]() та
та![]() правильні
раціональні дроби.
правильні
раціональні дроби.
Методика інтегрування раціональних ф-ій:
1. Якщо підінтегральна ф-ія – неправильний раціональний дріб, то за допомогою ділення його розкладають на суму многочлена і правильного раціонального дробу.
2. Знаменник правильного раціон. дробу розкладають на множники. По вигляду знаменника, правильний раціон. дріб представляють у вигляді найпростіших дробів, використовуючи метод невизначених коефіцієнтів.
3. Інтегрують цілу частину і найпростіші дроби.
Визначений інтеграл і його властивості
Якщо існує скінченна границя інтегральних сум Sn при і0 і не залежить ні від способу розбиття [a;b] на частини хі, ні від вибору точок і, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:
![]()
За означенням,
визначений інтеграл
![]() –
число, яке залежить від типу ф-іїf(x)
та проміжку [a;b]; він не залежить від
того, якою буквою позначена змінна
інтегрування.
–
число, яке залежить від типу ф-іїf(x)
та проміжку [a;b]; він не залежить від
того, якою буквою позначена змінна
інтегрування.
Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною.
1) Якщо
f(x)=c=const,
то
![]()
2) Сталий множник можна виносити з-під знака визначеного інтеграла.
3) Якщо f1(x)
та f2(x)
інтегровні
на [a;b], то:
![]()
4) Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл лише змінить свій знак на протилежний.
5) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю.
6) Якщо f(x)
– інтегровна в будь-якому із проміжків
[a;b], [a;c], [c;b], то:
![]()
7) Якщо f(x)0
і інтегровна для x[a,b],
b>a, то
![]()
8) Якщо f(x),
g(x) – інтегровні
та f(x)g(x)
для x[a;b],
b>a, то:
![]()
9) Якщо f(x) – інтегровна
та mf(x)M,
для x[a;b],
b>a, то
![]()
Задача, що призводить до поняття визначеного інтеграла
Обчислити площу криволінійної трапеції аАВв (рис. 7.4).
Розв’язання.
Розіб’ємо проміжок
[a;
b]
на n
частин точками
![]() так що
так що![]() Виберемо точки
Виберемо точки![]() так:
так:![]() Побудуємо прямокутники з основою
Побудуємо прямокутники з основою![]() і висотою
і висотою![]() (рис. 7.4).
(рис. 7.4).
Площа елементарного
прямокутника
![]() .
Площа ступінчастої фігури
.
Площа ступінчастої фігури![]() буде тим менше відрізнятись від площі
криволінійної трапеціїSaABb,
чим менша довжина
буде тим менше відрізнятись від площі
криволінійної трапеціїSaABb,
чим менша довжина
![]() ,
а в граничному випадку ці площі будуть
збігатися, тобто
,
а в граничному випадку ці площі будуть
збігатися, тобто![]()

Формула Ньютона-Лейбніца для обчислення визначених інтегралів
(Ньютона-Лейбніца): Якщо ф-ія f(x) – неперервна для x [a;b], то визначений інтеграл від ф-ії f(x) на проміжку [a;b] дорівнює приросту первісної ф-ії f(x) на цьому проміжку, тобто:
![]() де F’(x)=f(x)
де F’(x)=f(x)
Зв’язок між визначеним та невизначеним інтегралами можна представити такою рівністю:
 Наслідок:
Для обчислення визначеного інтеграла
достатньо знайти одну із первісних
підінтегральної ф-ії і виконати над нею
подвійну підстановку.
Наслідок:
Для обчислення визначеного інтеграла
достатньо знайти одну із первісних
підінтегральної ф-ії і виконати над нею
подвійну підстановку.
Метод безпосереднього інтегрування визначених інтегралів
Метод інтегрування заміни змінної у визначеному інтегралі
Якщо: 1)
![]() — неперервна для
— неперервна для![]() ;
2)
;
2)![]()
![]() 3)
3)![]() та
та![]() — неперервні для
— неперервні для![]() 4) при
4) при![]() то
то

 (7.13)
(7.13)
Зауваження. При заміні змінної інтегрування у визначеному інтегралі змінюються межі інтегрування, і тому нема потреби повертатись до початкової змінної.
Приклад.

=![]()
Метод інтегрування частинами у визначеному інтеграла
Теорема 11.
Якщо функції
![]() та
та![]() мають неперервні похідні для
мають неперервні похідні для![]() ,
то
,
то
![]()
Застосування визначеного інтеграла до обчислення площ фігур, обмежених лініями
Невласний інтеграл з нескінченною верхнею межею
Невласний інтеграл з нескінченною нижньою межею
Якщо
f(x)
— інтегровна для скінченних a
та b,
тобто
![]() формули для обчислення невласних
інтегралів на нескінченному проміжку
мають вигляд:
формули для обчислення невласних
інтегралів на нескінченному проміжку
мають вигляд:
![]()
Відмінність між невласними інтегралами І і ІІ роду
Невласний інтеграл ІІ роду
Якщо
існує скінченна границя
![]() ,
то її називають невласним інтегралом
ІІ роду і позначають
,
то її називають невласним інтегралом
ІІ роду і позначають![]() .
Якщо функція f(x) необмежена на [a,b], то
їїточки розриву можуть бути на лівому
кінці або на правому кінці, або всередині
проміжку інтегрування. У цих випадках
невласні інтеграли визначаються:
.
Якщо функція f(x) необмежена на [a,b], то
їїточки розриву можуть бути на лівому
кінці або на правому кінці, або всередині
проміжку інтегрування. У цих випадках
невласні інтеграли визначаються:![]() ,
,
![]() ,
,
![]() .
Якщо границі існують, то їх і називають
невласним інтегралом ІІ роду від функції
f(x) на відрізку [a;b]. Якщо границі не
існують, або є нескінченними, то невласний
інтеграл розбіжний
.
Якщо границі існують, то їх і називають
невласним інтегралом ІІ роду від функції
f(x) на відрізку [a;b]. Якщо границі не
існують, або є нескінченними, то невласний
інтеграл розбіжний
Метод найменших квадратів
Нехай х1, x2, … xn – послідовність значень незалеж змінної, а y1, y2, … yn – послідовн. значень залежної змінної. Необхідно підібрати пряму, яка найліпшим чином відображає залежність між х і у відхилення фактичних значень ф-ції від підібраної прямої має бути мінімальним. Нехай y=ax+b є рівн. цієї прямої y1=ax1+b1 … yn=axn=bn
Відхилення складає:
y1 – yi = yi – (axi + b) = yi – axi – b.
Це відхилення має бути додат або від’ємним, тому пряма підбирається так, щоб сума квадратів відхилень була найменшою. Необхідна умова існування min полягає в тому, що f/a = 0 f/b = 0.
Маємо: (y1-b-ax1)2=y12+b2+a2x12-2abxi-2bxiyi, отже:
![]()
Обчислимо: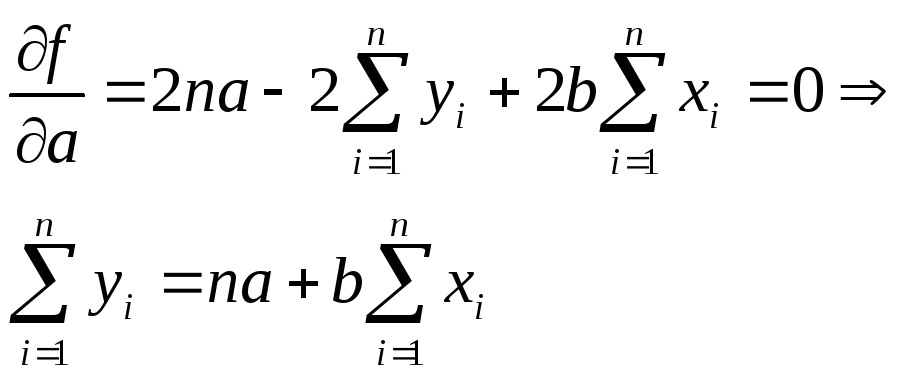
 Таким
чином ми отримали 2 рівн з двома змінними
a
і b.
Розв’язання цих двох рівн дає значення
a
і b,
які визначають пряму, яка найкраще
відображає хід змінної ф-ції.
Таким
чином ми отримали 2 рівн з двома змінними
a
і b.
Розв’язання цих двох рівн дає значення
a
і b,
які визначають пряму, яка найкраще
відображає хід змінної ф-ції.
Поняття ряду. Збіжність ряду та його сума
Нехай
![]() — деяка нескінченна послідовність
чисел. Побудований із цих чисел за
допомогою знака «+» символ
— деяка нескінченна послідовність
чисел. Побудований із цих чисел за
допомогою знака «+» символ
![]() (9.1)
(9.1)
називається
нескінченним
рядом (чи
просто рядом),
а самі числа
![]() — членами ряду;n-ий
член un
— називається загальним
членом ряду.
— членами ряду;n-ий
член un
— називається загальним
членом ряду.
Числовий ряд називається збіжним, якщо існує границя послідовності частинних сум ряду
![]() (9.3)
(9.3)
При цьому величина
![]() називається сумою ряду, а число
називається сумою ряду, а число
![]() — (9.4)
— (9.4)
залишком ряду. Якщо границя Sn не існує (нескінченна), то ряд називається розбіжним.
Побудуємо частинні суми ряду:
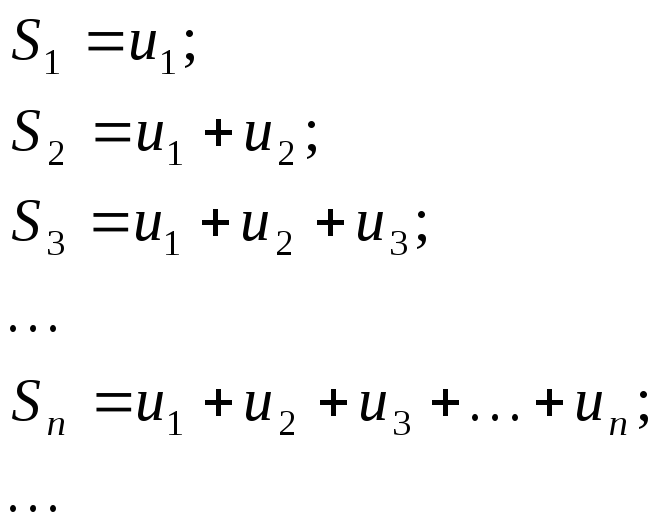 (9.2)
(9.2)
Частинні суми ряду
(9.2) утворюють числову послідовність:
![]() Надалі основним буде питання про
збіжність послідовності частинних сум
ряду. Таким чином, поняття ряду вводиться
для побудови числових послідовностей
спеціального виду — частинних сум ряду.
Такі послідовності широко використовуються
в математичному аналізі, наприклад,
відоме числое
можна подати таким рядом
Надалі основним буде питання про
збіжність послідовності частинних сум
ряду. Таким чином, поняття ряду вводиться
для побудови числових послідовностей
спеціального виду — частинних сум ряду.
Такі послідовності широко використовуються
в математичному аналізі, наприклад,
відоме числое
можна подати таким рядом
![]() .
.
Властивості збіжних рядів
Теорема 1. Якщо збігається ряд, то збігається його залишок; і навпаки, із збіжності залишку випливає збіжність ряду.
Наслідок 1. Із розбіжності ряду випливає розбіжність його залишку, і навпаки.
Наслідок 2. Якщо відкинути скінченну кількість перших членів ряду або додати до нього кілька нових членів, то це не вплине на його збіжність.
Теорема 2. Якщо члени збіжного ряду (9.1) помножити на сталий множник с, то його збіжність не порушиться, а сума (9.3) помножиться на це число с:
![]() .
.
Теорема
3.
Збіжні ряди
![]() і
і![]() можна почленно додавати або віднімати,
при цьому ряд
можна почленно додавати або віднімати,
при цьому ряд![]()
![]() також збігається, а його сума буде
також збігається, а його сума буде![]() .
.
Теорема 4. Послідовність частинних сум збіжного ряду обмежена. Це твердження випливає зі збіжності послідовності частинних сум ряду.
Теорема
5.
Якщо ряд збігається, то границя його
загального члена прямує до 0, тобто:
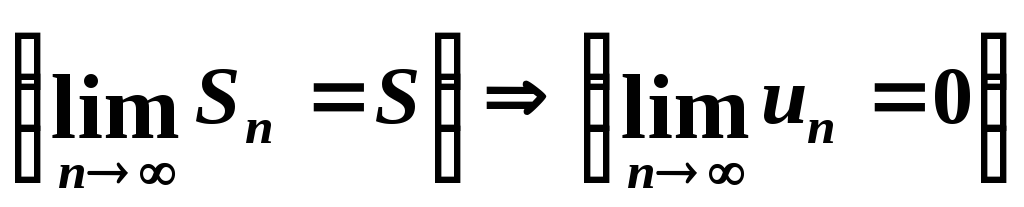 .
.
Наслідок.
Якщо
![]() ,
тобто необхідна умова збіжності ряду
не виконується, то ряд розбігається.
,
тобто необхідна умова збіжності ряду
не виконується, то ряд розбігається.
Необхідна ознака збіжності ряду
Якщо ряд
збігається, то границя його загального
члена при n прямує до нескінченності
дорівнює нулю, тобто
![]() .
Якщо
.
Якщо![]() або не існує, то ряд
або не існує, то ряд![]() розбіжний.
розбіжний.
Еталонні ряли
Достатні ознаки збіжності додатних числових рядів. Ознака порівняння
Розглянемо
ряд
![]() з додатними членами
з додатними членами![]()
![]() .
Частинні суми ряду (9.2) утворюють при
цьому монотонно зростаючу послідовність
.
Частинні суми ряду (9.2) утворюють при
цьому монотонно зростаючу послідовність![]() .
.
Теорема 6 (основна). Для того щоб ряд з додатними членами збігався, необхідно і достатньо, щоб усі його частинні суми були обмеженими.
Наслідок. Для того щоб ряд з додатними членами розбігався, необхідно і достатньо, щоб послідовність його частинних сум була необмеженою.
Теорема. 7 (ознака порівняння рядів). Якщо для рядів з додатними членами:
![]() (9.6)
(9.6)
![]() (9.7)
(9.7)
виконується умова
![]() то:
то:
а) із збіжності ряду (9.7) випливає збіжність ряду (9.6);
б) із розбіжності ряду (9.6) випливає розбіжність ряду (9.7).
Означення.
Якщо для
рядів (9.6), (9.7) виконується умова
![]() ,
то ряд (9.7) називаєтьсямажорантним
відносно ряду (9.6), а ряд (9.6) — мінорантним
відносно ряду (9.7).
,
то ряд (9.7) називаєтьсямажорантним
відносно ряду (9.6), а ряд (9.6) — мінорантним
відносно ряду (9.7).
Гранична ознака порівняння
Якщо для
рядів з додатними членами (9.6), (9.7) існує
границя
![]() ,
то ряди (9.6) і (9.7) збігаються або розбігаються
разом.
,
то ряди (9.6) і (9.7) збігаються або розбігаються
разом.
Ознака Даламбера
Якщо для ряду
![]() з додатними членами
з додатними членами![]() існує границя
існує границя![]() тоді:
тоді:
при
![]() ряд збігається;
ряд збігається;
при
![]() ряд розбігається;
ряд розбігається;
при
![]() питання про збіжність ряду ознака не
вирішує
питання про збіжність ряду ознака не
вирішує
Радикальна ознака Коші
Якщо для ряду
![]() з додатними членами
з додатними членами![]() існує границя
існує границя![]() ,
тоді:
,
тоді:
при
![]() ряд збігається;
ряд збігається;
при
![]() ряд розбігається;
ряд розбігається;
при
![]() питання про збіжність ряду ознака не
вирішує.
питання про збіжність ряду ознака не
вирішує.
Інтегральна ознака Коші
Якщо функція
![]() неперервна, додатна і монотонно спадає
при
неперервна, додатна і монотонно спадає
при![]() то ряд
то ряд![]() і невластивий інтеграл
і невластивий інтеграл![]() збігаються або розбігаються разом.
збігаються або розбігаються разом.
Знакозмінні ряди. Ознака Лейбніца
Ряд називається знакозмінним, якщо він містить нескінченне число як додатних, так і від’ємних членів.
Якщо члени
знакопочергового ряду спадають за
абсолютною величиною і границя
абсо-
лютної величини загального члена
ряду дорівнює нулю, то ряд збігається.
Коротко цю теорему можна записати так:
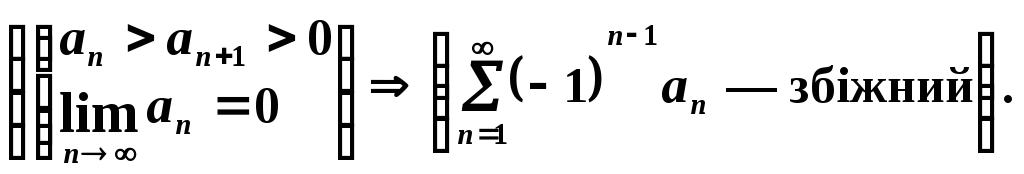
Наслідок 1.
Знак суми
збіжного знакопочергового ряду такий
само, як і знак першого члена ряду (на
рис. 9.1
![]() ).
).
Геометрична інтерпретація

Рис. 9.1
Наслідок
2.
Якщо знакопочерговий ряд збігається,
то його сума за абсолютною величиною
не перевищує першого члена ряду, тобто
![]() (на рис. 9.1) 0<S <a1).
(на рис. 9.1) 0<S <a1).
Наслідок 3.
Якщо при
обчисленні суми збіжного знакопочергового
ряду обмежитись тільки першими n
членами, а всі інші відкинути, то похибка
за абсолютною величиною не перевищить
першого із відкинутих членів, тобто
![]() .
.
Наслідок 4.
Якщо для ряду
не виконується умова теореми Лейбніца
![]() ,
то ряд розбігається (не виконується
необхідна умова збіжності).
,
то ряд розбігається (не виконується
необхідна умова збіжності).
Абсолютна та умовна збіжність рядів
Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду.
Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається.
Якщо знакозмінний ряд збігається абсолютно, то його збіжність зумовлена достатнім спаданням за абсолютною величиною його членів
Якщо знакозмінний ряд збігається умовно, то його збіжність зумовлена не тільки спаданням за абсолютною величиною його членів, але і взаємною компенсацією додатних і від’ємних членів ряду.
Функціональні ряди. Основні поняття
Ряд
![]() , (9.10)
, (9.10)
де членами
ряду
![]() є функції від аргументух,
називається
функціональним
рядом.
При х=х0
ряд (9.10) перетворюється на числовий
є функції від аргументух,
називається
функціональним
рядом.
При х=х0
ряд (9.10) перетворюється на числовий
![]() (9.11)
(9.11)
Якщо ряд (9.11) збігається (розбігається), то кажуть, що при х=х0 збігається (розбігається) функціональний ряд
Усі значення аргументу х, при яких функціональний ряд збіжний, називаються областю збіжності функціонального ряду.
В області збіжності існує границя часткових сум функціонального ряду
![]() ,
,
де функція
![]() — сума ряду.
— сума ряду.
Ряд
![]() називаєтьсязалишком
ряду.
називаєтьсязалишком
ряду.
В області
збіжності функціонального ряду
виконується формула
![]() ,
де
,
де![]() .
.
Ряд (9.11) збіжний
для всіх х
із області Х,
називається рівномірно
збіжним у
цій області, якщо для будь-якого числа
![]() існує такий незалежний відх
номер N,
що при n
> N
виконується одночасно для всіх
існує такий незалежний відх
номер N,
що при n
> N
виконується одночасно для всіх
![]() така нерівність:
така нерівність:
![]()
Степеневі ряди. Основні поняття. Теорема Абеля
Функціональний ряд
![]() (9.12)
(9.12)
називається
степеневим
рядом,
його загальний член
![]() ;числа
;числа
![]() називаютьсякоефіцієнтами
степеневого ряду.
називаютьсякоефіцієнтами
степеневого ряду.
Розглядають і більш загальний вигляд степеневого ряду
![]() (9.13)
(9.13)
Якщо в (9.13) візьмемо х – с = у, то дістанемо ряд типу (9.12), тому властивості ряду (9.12) неважко перефразувати і для ря- ду (9.13).
Теорема 14 (Абеля). Якщо степеневий ряд (9.12):
1) збігається
при х
= х0,
то він абсолютно збігається для будь-якого
х,
що задовольняє нерівність
![]() ;
;
2) якщо
ряд (9.12) розбігається при х
= х1,
то він розбігається при всіх х,
що задовольняють нерівність
![]() .
.
Радіус, інтервал, область збіжності ряду
Інтервалом
збіжності степеневого ряду називається
такий інтервал, у всіх внутрішніх точках
якого ряд збігається абсолютно, а для
всіх точок
![]() ряд є розбіжним; при цьому числоR > 0
називається радіусом збіжності
степеневого ряду.
ряд є розбіжним; при цьому числоR > 0
називається радіусом збіжності
степеневого ряду.
Для
узагальненого степеневого ряду (9.13)
інтервал збіжності
![]() має центр симетрії в точціх
= с.
має центр симетрії в точціх
= с.
Радіус збіжності визначається за формулою
![]() .
.
Аналогічно,
використовуючи радикальну ознаку Коші,
можна дістати формулу для радіуса
збіжності, степеневого ряду у вигляді:
 .
.
Усі значення аргументу х, при яких функціональний ряд збіжний, називаються областю збіжності функціонального ряду.
В області збіжності існує границя часткових сум функціонального ряду
![]() ,
,
де функція
![]() — сума ряду.
— сума ряду.
Ряд
![]() називаєтьсязалишком
ряду.
називаєтьсязалишком
ряду.
В області
збіжності функціонального ряду
виконується формула
![]() ,
де
,
де![]() .
.
Ряд Тейлора
Формули, що подають функцію f(x) у вигляді степеневих рядів, мають вигляд:
![]()
(9.18)
Кажуть, що ряд Тейлора (9.18) — дає розвинення функції в ряд поблизу точки х = с. Справді, як далі буде показано, чим ближче х до точки розвинення функції f(x) у ряд, тим меншою кількістю членів ряду буде досягнуто більшої точності при обчисленні f(x).
Ряд Маклорена
![]() (9.17)
(9.17)
Кажуть, що ряд Маклорена (9.17) дає розвинення функції в ряд поблизу точки х = 0
Справді, як далі буде показано, чим ближче х до точки розвинення функції f(x) у ряд, тим меншою кількістю членів ряду буде досягнуто більшої точності при обчисленні f(x).
Теорема
15
(достатня
умова розвинення функції в ряд Маклорена).
Якщо
на проміжку
![]() похідні будь-якого порядку для функціїf(x)
обмежені одним і тим самим числом
похідні будь-якого порядку для функціїf(x)
обмежені одним і тим самим числом
![]() то на інтервалі
то на інтервалі![]() функціяf(x)
може бути розвинена в ряд Маклорена).
Іншими словами, ряд Маклорена для f(x)
у кожній точці із
функціяf(x)
може бути розвинена в ряд Маклорена).
Іншими словами, ряд Маклорена для f(x)
у кожній точці із
![]() збігається абсолютно.
збігається абсолютно.
Залишок
ряду Маклорена
![]() можна замінити одним залишковим членом
можна замінити одним залишковим членом![]() ,
який у формі Лагранжа такий:
,
який у формі Лагранжа такий:
![]() (9.19)
(9.19)
Тоді ряд Маклорена (9.17) набирає вигляду формули Маклорена
![]() (9.20)
(9.20)
Теорема
16.
Для того щоб функцію f(x)
можна було розвинути в ряд Маклорена
на інтервалі
![]() ,
необхідно і достатньо, щоб на цьому
інтервалі
,
необхідно і достатньо, щоб на цьому
інтервалі![]()
Використання рядів до наближених обчислень функції
Використання рядів до наближених обчислень визначених інтегралів
Диференціальні рівняння. Основні поняття та означення
Диф. Рівнянням називається рівняння, яке містить шукану похідну ф-ції. Найбільший порядок похідних називається порядком диференційного рівняння. Найб. порядок пох. наз. порядком диф. р-ня.
Звич. ДР наз. нетотож. співвіднош. між шуканою ф-цією однієї змінної самою не залеж. змінною та пох. шук. ф-ції певних порядків.
Розв’язком ДР y’=f(x;y) наз. ф-ція у=(х), яка при підстановці у ДР перетвор. його у тотож.
Розвязок, що містить довільні пост. наз загальним роз. ДР.
Розв., який одерж. із заг. При деяких дов. знач. дов. постійних наз. част. розв.
Диференціальні рівняння першого порядку. Основні поняття
|
|
— ДР першого порядку; |
Диференціальні рівняння з відокремлюваними змінними
Д.Р. вигляду M(x)dx+N(y)dy=0 називаються Д.Р. з відокремленими змінними. Загальний розв’язок має вигляд:
M(x)dx+N(y)dy=C і розв. Задачі Коші з початковими умовами х=х0, у=у0 має вигляд:
![]() .
.
Д.Р. виду N1(y)M1(x)dx+M2(x)N2(y)dy=0 називаються Д.Р. з відокремлюваними змінними, тобто рівняння, що зводяться до рівнянь з відокремленими змінними.
Задача Коші
Розгл. ДР y’=f(x;y).
Задача пошуку розв. у=(х), що задов. умови у=у0 при х=х0 наз. задачею Коші. Умови наз. початковими, а у0, х0 – поч. знач.
Однорідні диференціальні рівняння першого порядку
Д.Р. називається однорідним, якщо його можна подати у вигляді:
![]()
Воно за допомогою заміни змінної y/x=u y=ux зводиться до Д.Р. з відокремлюваними змінними.
![]()
та знаходження розв’язку зводиться до квадратур:
![]()
Лінійні диференціальні рівняння першого порядку
Диференціальні рівняння виду
![]() (8.29)
(8.29)
називається
лінійним
ДР.
Якщо
![]() ,
то ДР є однорідним. Якщо
,
то ДР є однорідним. Якщо![]() ,
то ДР називаєтьсянеоднорідним.
,
то ДР називаєтьсянеоднорідним.
Однорідні рівняння інтегруються у квадратурах, як ДР із відокремленими змінними:
![]() ,
,
![]()
![]()
![]() .
.
Диференціальні рівняння другого порядку. Основні поняття
У загальному випадку ДР другого порядку має вигляд
![]()
Загальний розв’язок рівняння містить дві довільні сталі:
![]() (8.32)
(8.32)
і за
рахунок вибору довільних сталих
![]() можна розв’язати задачу Коші, яка
полягає в пошуку частинного розв’язку
можна розв’язати задачу Коші, яка
полягає в пошуку частинного розв’язку![]() ,
що задовольняє початкові умови
,
що задовольняє початкові умови![]()
Для ДР
другого порядку частіше зустрічається
на практиці крайова задача, коли умова
на шуканий розв’язок
![]() задається при різних значеннях аргументу.
задається при різних значеннях аргументу.
Диференціальні рівняння другого порядку, що допускають пониження порядку
У деяких випадках можна знизити порядок ДР другого порядку (8.31) і звести до ДР першого порядку.
І. У ДР відсутня шукана функція. ДР виду
![]() (8.33)
(8.33)
зводяться
до ДР першого порядку, якщо візьмемо
![]() Дістанемо ДР першого порядку
Дістанемо ДР першого порядку
![]() (8.34)
(8.34)
Якщо
буде знайдено загальний розв’язок
цього рівняння
![]() то дістанемо
то дістанемо![]()
Якщо ДР
другого порядку має вигляд
![]() то беремо
то беремо![]() і дістаємо ДР першого порядку
і дістаємо ДР першого порядку![]() з відокремлюваними змінними:
з відокремлюваними змінними:
![]()
Рівняння Бернуллі
Рівняння Бернуллі
Диференціальне рівняння виду
![]() ,
(12.24)
,
(12.24)
в
якому
![]() неперервні
функції, а число
неперервні
функції, а число![]() відмінне
від
відмінне
від
нуля
та одиниці, називається рівнянням
Бернуллі (при
![]()
маємо
лінійне рівняння, а при
![]() -
рівняння з відокремлюваними
-
рівняння з відокремлюваними
змінними).
Покажемо,
що рівняння Бернуллі зводиться до
лінійного диференціального рівняння
першого порядку. Для цього поділимо
ліву й праву частини рівняння (12.24) на
у^n та
виконаємо заміну змінної
![]() .
Оскільки
.
Оскільки
![]() ,
диференціальне
рівняння Бернуллі перетворюється на
рівняння
,
диференціальне
рівняння Бернуллі перетворюється на
рівняння
![]()
яке
є лінійним. Проінтегрувавши його одним
з описаних раніше способів і повернувшись
від
![]() до
попередньої змінної
до
попередньої змінної![]() ,
можна отримати розв’язок рівняння
Бернуллі.
,
можна отримати розв’язок рівняння
Бернуллі.
Зауважимо, що зручніше розв’язувати рівняння Бернуллі, не зводячи його до лінійного, за допомогою підстановки y=u*v, тобто так само, як і лінійне неоднорідне рівняння.
Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами
В загальному випадку Д.Р. ІІ порядку має вигляд F(x,y,y’,y’’)=0. Загальний розв’язок рівняння містить 2 довільні сталі y=(x,C1,C2) і за рахунок вибору C1 і С2 можна розв’язати задачу Коші, яка полягає в пошуку частинного розв’язку y=y(x), що задовольняє початковій умові y(x0)=y0, y’(x0)=y0’.
Однорідні.
Означення: Рівняння вигляду y’’+a1y’+a2y=0 називаються однорідними лінійними Д.Р.
Розв’язок:
y’’+a1y’+a2y=0
Складаємо характеристичне рівняння:
K2+a1K+a2=0
А) D>0
![]()
Б) D=0, K1,2= –b/2
![]()
В) D<0, K1,2 – комплексні числа. K1,2=XI
![]()
Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
Лінійні
неоднорідні диференціальні рівняння
другого порядку із сталими коефіцієнтами
називається
рівняння виду
![]() ,
де p, q – сталі величини, f(x) – задана
функція, неперервна на деякому проміжку
(a;b). Загальним розв`язком рівняння
,
де p, q – сталі величини, f(x) – задана
функція, неперервна на деякому проміжку
(a;b). Загальним розв`язком рівняння![]() є
сума його довільного частинного розв`язку
і загального розв`язку відповідного
однорідного рівняння
є
сума його довільного частинного розв`язку
і загального розв`язку відповідного
однорідного рівняння![]() ,
тобто
,
тобто![]() ,
де
,
де
![]() - загальний розв`язок однорідного
рівняння,
- загальний розв`язок однорідного
рівняння,
![]() -
частинний розв`язок неоднорідного
рівняння. Для знаходження частинного
розв`язку неоднорідних рівнянь існує
два методи: метод варіації довільних
сталих і метод невизначених коефіцієнтів.
-
частинний розв`язок неоднорідного
рівняння. Для знаходження частинного
розв`язку неоднорідних рівнянь існує
два методи: метод варіації довільних
сталих і метод невизначених коефіцієнтів.
Метод невизначених коефіцієнтів при розв`язуванні лінійних неоднорідних диференціальних рівнянь другого порядку
