Практичне заняття 16. Статистичні оцінки параметрів розподілу

Приклад. За заданим інтервальним статистичним розподілом вибірки

h = 8	0-8	8-16	16-24	24-32	32-40	40-48
ni	10	15	20	25	20	10
Wi	0,1	0,15	0,2	0,25	0,2	0,1

потрібно побудувати гістограму частот і відносних частот.

Розв’язання.Гістограми частот і відносних частот наведені на рис. 109, 110.

Рис. 109

Площа гістограми частот

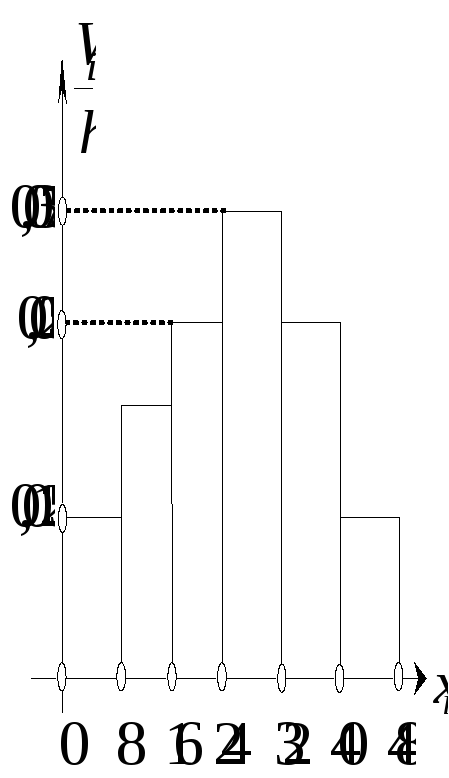
Рис. 110

Приклад. За заданим інтервальним статистичним розподілом вибірки

h=4	0-4	4-8	8-12	12-16	16-20	20-24
ni	6	14	20	25	30	5

побудувати гістограму частот і F ^(x).

Визначити Mo^, Me^.

Розв’язання.Гістограма частот зображена на рис. 113.

Рис. 113

Графік F ^(x) зображено на рис. 114.

Рис. 114

З рис. 113 визначається модальний інтервал, який дорівнює 16-20.

Застосовуючи (362) і беручи до уваги, що ,,,h=4,, дістанемо

;

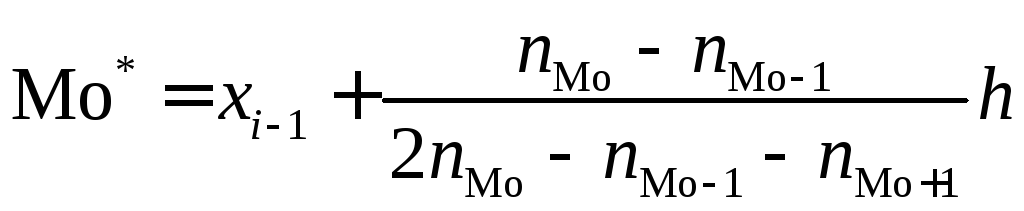Отже, Mo^ = 16,17.

З графіка F^(x) визначається медіанний інтервал, який дорівнює 12-16.

Беручи до уваги, що F(12) = 0,4,F(16) = 0,65,h= 4 i застосовуючи (361), дістанемо:

Отже, = 13,6.

Приклад. За заданим інтервальним статистичним розподілом вибірки, в якому наведено розподіл маси новонародженихх_і,

, кг	1-1,2	1,2-1,4	1,4-1,6	1,6-1,8	1,8-2	1,8-2	2-2,2	2,4-2,6	2,6-2,8	2,8-3	3-3,2
пі	5	12	18	22	36	24	19	15	11	9	2

обчислити

Розв’язання.Побудуємо дискретний статистичний розподіл за заданим інтервальним. Оскількиh= 0,2, то дістанемо:

	1,1	1,3	1,5	1,7	1,9	2,1	2,3	2,5	2,7	2,9	3,1
hi	5	12	18	22	36	24	19	15	11	9	2

Беручи до уваги (363), (364), (365) і те, що n= 173, дістанемо:

.

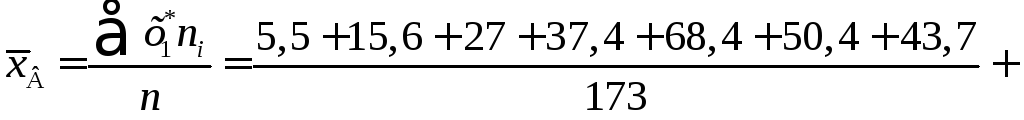
Отже, .

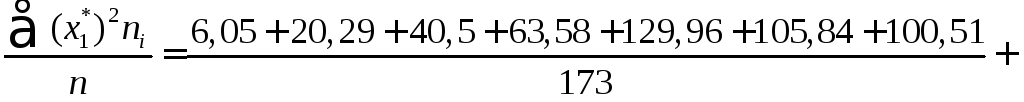
= 0,217149.

Отже, кг.

Практичне заняття 17. Довірчі інтервали

1. Довірчий інтервал для оцінки математичного сподівання нормального розподілу при відомому .

2. Довірчий інтервал для оцінки математичного сподівання нормального розподілу при невідомому .

Приклад.Вимірявши 40 випадково відібраних після виготовлення деталей, знайшли вибіркову середню, що дорівнює 15 см. Із надійністюпобудувати довірчий інтервал для середньої величини всієї партії деталей, якщо генеральна дисперсія дорівнює.

Розв’язання.Для побудови довірчого інтервалу необхідно знати:,n,x.

З умови задачі маємо: Величинахобчислюється з рівняння

Знайдемо числові значення кінців довірчого інтервалу:

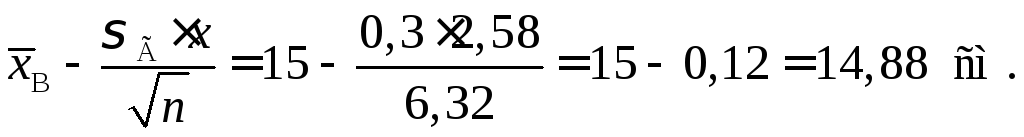
Таким чином, маємо:

.

Приклад.Маємо такі дані про розміри основних фондів (у млн грн.) на 30-ти випадково вибраних підприємствах:

4,2; 2,4; 4,9; 6,7; 4,5; 2,7; 3,9; 2,1; 5,8; 4,0;

2,8; 7,8; 4,4; 6,6; 2,0; 6,2; 7,0; 8,1; 0,7; 6,8;

9,4; 7,6; 6,3; 8,8; 6,5; 1,4; 4,6; 2,0; 7,2; 9,1.

Побудувати інтервальний статистичний розподіл із довжиною кроку h = 2 млн грн.

З надійністю знайти довірчий інтервал для, якщо= 5 млн грн.

Розв’язання.Інтервальний статистичний розподіл буде таким:

h = 2 млн грн.	2–4	4–6	6–8	8–10
ni	9	7	10	4

Для визначення необхідно побудувати дискретний статистичний розподіл, що має такий вигляд:

	3	5	7	9
ni	9	7	10	4

.

Тоді

Для побудови довірчого інтервалу із заданою надійністю необхідно знайтих:

Обчислюємо кінці інтервалу:

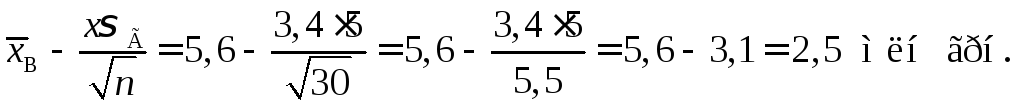
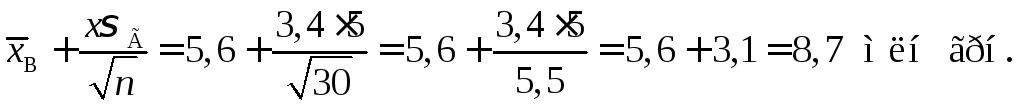
Отже, довірчий інтервал для буде.

Приклад.Якого значення має набувати надійність оцінки γ, щоб за обсягу вибіркиn = 100 похибка її не перевищувала 0,01 при.

Розв’язання.Позначимо похибку вибірки

Далі маємо:

Як бачимо, надійність мала.

Приклад. Визначити обсяг вибіркиn, за якого похибкагарантується з імовірністю 0,999, якщо.

Розв’язання.За умовою задачіОскільки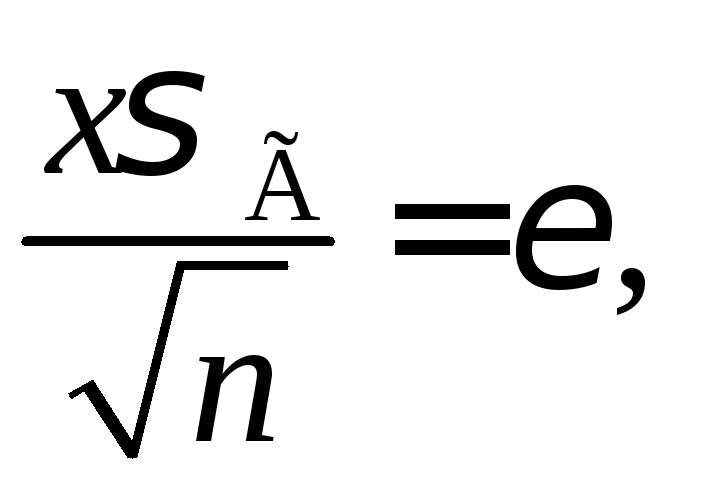то дістанемо: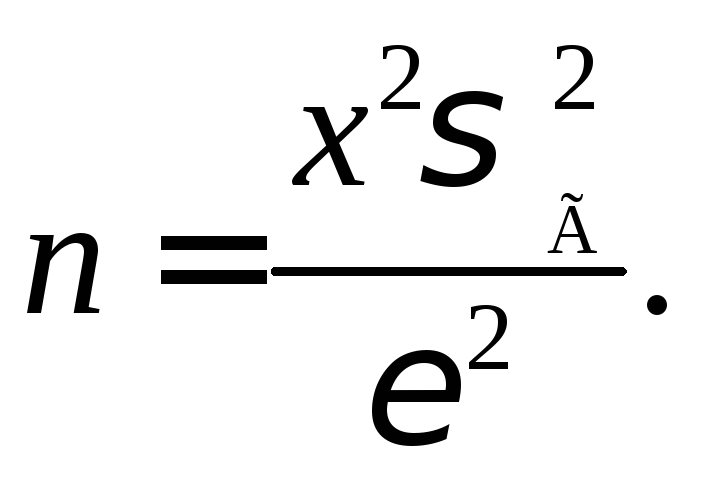Величинухзнаходимо з рівностіТоді

Приклад.Випадково вибрана партія з двадцяти приладів була випробувана щодо терміну безвідмовної роботи кожного з нихt_і. Результати випробувань наведено у вигляді дискретного статистичного розподілу:

ti	100	170	240	310	380
ni	2	5	10	2	1

З надійністю побудувати довірчий інтервал для «а» (середнього часу безвідмовної роботи приладу).

Розв’язання.Для побудови довірчого інтервалу необхідно знайти середнє вибіркове і виправлене середнє квадратичне відхилення.

Обчислимо :

Отже, дістали

Визначимо D_B:

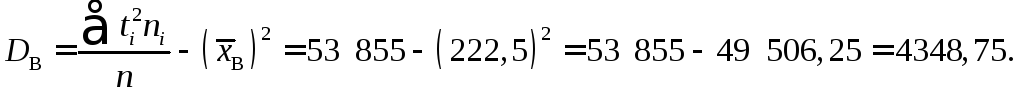
Отже, D_B = 4348,75.

Виправлене середнє квадратичне відхилення дорівнюватиме:

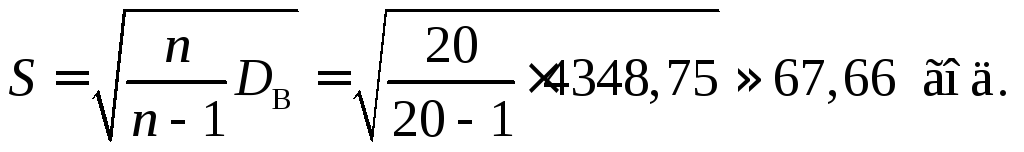
За таблицею значень (додаток 3) розподілу Ст’юдента за заданою надійністюі числом ступенів свободи= 20 – 1 = 19 знаходимо значення

Обчислимо кінці довірчого інтервалу:

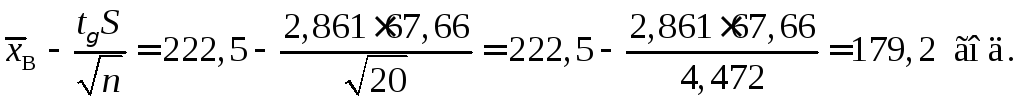
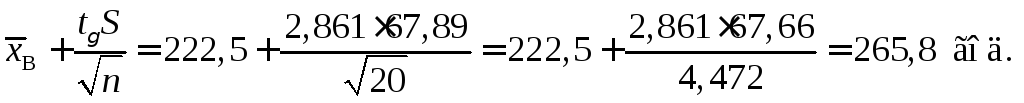
Отже, з надійністю можна стверджувати, щобуде міститися в інтервалі.

При великих обсягах вибірки, а саме: на підставі центральної граничної теореми теорії ймовірностей (теореми Ляпунова) розподіл Ст’юдента наближається до нормального закону. Уцьому разі знаходиться за таблицею значень функції Лапласа.

Приклад. У таблиці наведено відхилення діаметрів валиків, оброблених на верстаті, від номінального розміру:

h= 5 мк	0–5	5–10	10–15	15–20	20–25
ni	15	75	100	50	10

Із надійністю побудувати довірчий інтервал для.

Розв’язання. Для побудови довірчого інтервалу необхідно знайти,S.

Для цього від інтервального статистичного розподілу, наведеного в умові задачі, необхідно перейти до дискретного, а саме:

	2,5	7,5	12,5	17,5	22,5
ni	15	75	100	50	10

Обчислимо :

Отже,

Визначимо D_B:

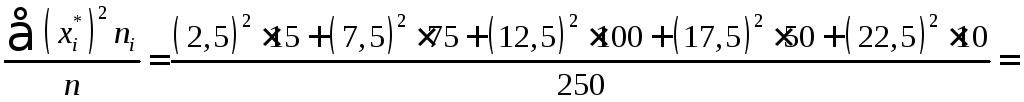
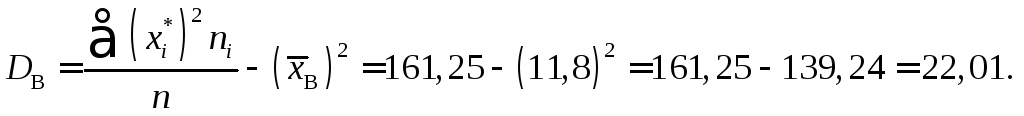
Обчислимо виправлене середнє квадратичне відхилення S:

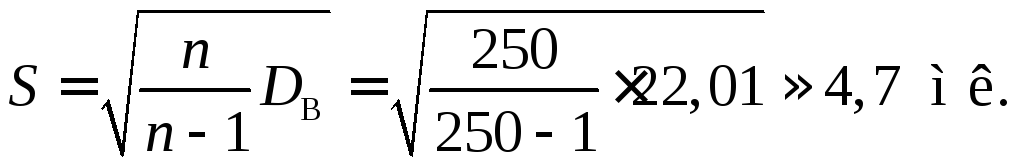
З огляду на великий (n = 250) обсяг вибірки можна вважати, що розподіл Ст’юдента близький до нормального закону. Тоді за таблицею значення функції Лапласа

Обчислимо кінці інтервалів:

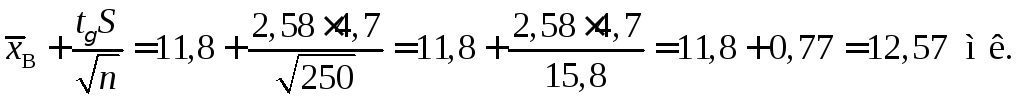
Отож, довірчий інтервал для середнього значення відхилень буде таким: .

Звідси з надійністю (99%) можна стверджувати, щоа [11,03 мк; 12,57 мк].