Міністерство освіти і науки україни

ПОЛТАВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

імені ЮРІЯ КОНДРАТЮКА

Кафедра комп’ютерних та інформаційних технологій і систем

ТЕОРІЯ ЙМОВІРНОСТЕЙ, ЙМОВІРНІСНІ ПРОЦЕСИ І

МАТЕМАТИЧНА СТАТИСТИКА

Практичні заняття

Напрям підготовки (спеціальність) 6.050101 Комп’ютерні науки

Укладач:

ст. викладач Руденко О.А.

Полтава

2010

ПРАКТИЧНЕ ЗАНЯТТЯ 1. АЛГЕБРА ПОДІЙ. ЙМОВІРНІСТЬ ПОДІЙ

1. Алгебра подій.

2. Ймовірність подій.

Задача. У ящику містяться кульки білого та чорного кольору. Навмання з нього виймають одну кульку. Подія А = {вийнято кульку білого кольору}, подія В = {вийнято кульку чорного кольору}. Сумісні чи несумісні ці події?

Розв’язання. Ці події несумісні, тому що поява події А виключає можливість появи події В, і навпаки. У даному випробуванні події А і В є протилежними:

, .

Задача. Підкидають два гральних кубики. Нехай події – {випаде і очок на першому кубику}, і = 1,2,3,4,5,6, – {випаде очок на другому кубику}, = 1,2,3,4,5,6. Виразити через , такі події:

а) сума очок на двох кубиках дорівнює п’яти;

б) випаде в сумі хоча б десять очок;

в) випаде в сумі не більше трьох очок.

Розв’язання. а) Нехай = {сума очок на двох кубиках дорівнює п’яти}. Ця подія можлива лише тоді, коли на першому кубику випаде і очок, а на другому – очок так, щоб і+ = 5, тобто і = 1, = 4, або і = 2, = 3, або і = 3, = 2, або і = 4, = 1. Отже,

б) Позначимо = {випаде в сумі хоча б десять очок}. Подія С₂ відбудеться тоді, коли на двох кубиках у сумі випаде або 10, або 11, або 12 очок, тобто і = 4, = 6, або і = 5, = 5, або і = 6, = 4, або і = 6, =5, або і = 5, = 6, або і = 6, = 6. Тому

.

В) Нехай = {випаде в сумі не більше трьох очок}. Оскільки найменша кількість очок, яка може випасти на кожному кубику, дорівнює одиниці, то подіяможлива лише тоді, коли сума очок на двох кубиках дорівнюватиме або двом, або трьом. Тому

.

Задача. Два стрільці роблять постріл у мішень по одному разу. Подія А = {у мішень влучив перший стрілець}, подія В ={у мішень влучив другий стрілець}. Виразити через А і В такі події: С = {два влучення в мішень}, = {жодного влучення в мішень}, Е = {хоча б одне влучення в мішень}, = {лише одне влучення в мішень}.

Розв’язання. Простір елементарних подій складається з чотирьох подій

, ,,

Подія С відбудеться тоді, коли обидва стрільці влучать у мішень. Тому вона є добутком двох подій А і В. Отже,

.

Подія D полягає в тому, що в мішень не влучить жодний стрілець, тобто не влучить ані перший (А), ані другий (В). Тому

.

Подія Е відбудеться тоді, коли в мішень влучить хоча б один стрілець. Це може бути тоді, коли або обидва стрільці влучать у мішень, або перший влучить, другий не влучить, або перший не влучить, а другий влучить. Тому

,

тобто

Е = А + В.

Подія F полягає в тому, що перший стрілець влучить у мішень, а другий не влучить або другий влучить, а перший не влучить. Тому

.

Задача. Партія складається з 10 стандартних (С) і 5 нестандартних (Н) деталей. Із партії навмання беруть 5 деталей. Знайти ймовірність того, що серед узятих деталей 3 виявились стандартними.

Розв’язання. Подія А – «серед 5 деталей 3 стандартні, а 2 нестандартні». Деталі беруться навмання, тому можливою елементарною подією є будь-яка група з 5 деталей, вибраних із 15 деталей. Щоб визначити, до якого типу підмножин належать ці групи, розглянемо одну з них. Нехай у групі виявилося 2 стандартні і 3 нестандартні деталі, тобто маємо . Виконаємо у групі довільне переставлення, наприкладГрупа не змінилась – у ній як було, так і залишилося 2 стандартні деталі. Отже, порядок у групі неістотний, тому такі групи належать до комбінацій. Усі елементарні події рівноможливі, для обчислення ймовірності застосуємо формулу класичного означення ймовірності.

Загальна кількість елементарних подій

Щоб обчислити кількість елементарних подій, які становлять подію А, міркуємо так: 3 стандартні деталі з 10 можна вибратиспособами, а 2 нестандартні з 5 –способами. Отже,

Остаточно дістаємо:

Задача. Протягом зміни приймальник прийняв у ремонт 10 годинників тієї самої марки від 10 різних осіб і перед закінченням зміни навмання розклав їх підряд на круглій полиці. Знайти ймовірність того, що три годинники, які належать певним особам, виявились поруч.

Розв’язання. ПодіяА– «три годинники, які належать певним особам, виявились поруч». Усі 10 годинників розкладались навмання, тому вони могли розміститися в довільному порядку. Отже, можлива елементарна подія – переставлення. Загальна кількість елементарних подій дорівнює кількості переставлень із10 елементів. Усі вони рівноможливі і несумісні. Тому можна застосувати класичне означення ймовірності. Згідно зі сказанимЩоб обчислитиm, об’єднаємо 3 годинники певних осіб в одну групу. Тоді для подіїАбуде 7! переставлень серед 7 годинників, які залишились; 3! переставлень буде у групі відібраних годинників, а крім того, група із 3 годинників може бути розміщена в будь-якому із 7 проміжків між 7 годинниками, які залишились. Отже,

Задача. Двоє осіб домовились зустрітися в певному місці у проміжку часу відгодин, а також про те, що той, хто прийде першим, чекатиме на другого протягомtгодин. Знайти ймовірність того, що зустріч відбудеться, якщо кожна особа може прийти в довільний момент часуt

Розв’язання. Подія А – «зустріч відбудеться». Позначимо довжину часового проміжкуа моменти приходу кожноїособи – Тоді подіяА відбудеться за умови деЗобразимо ці умови на площині в системі координат(рис. 1). Як випливає з рис. 1, часуТвідповідає площа квадратаа подіїА— площа шестикутникаСкориставшись геометричним означенням імовірності, дістанемо: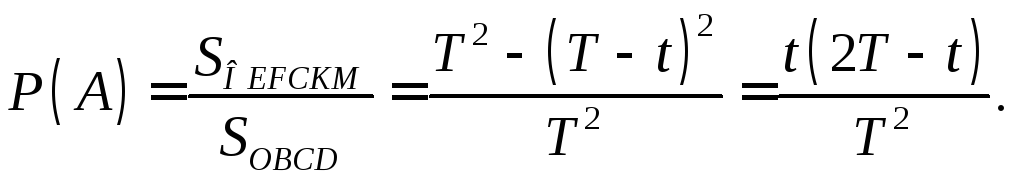

Задача. На двох суміжних сторонах квадрата з довжиною сторони, що дорівнює 1, навмання взято по точці. Знайти ймовірність того, що відстань між цими точками не перевищить 0,5.

Розв’язання.ПодіяА– «відстань між двома навмання взятими точками не перевищить 0,5». Позначимо відстань від точок, узятих на сторонах квадрата, до його вершини, що є спільною для цих сторін, черезТоді відстань між зазначеними точкамиМножина значень длянезліченна, причому значення кожної з цих змінних рівноможливі на заданих відрізках. Для обчислення ймовірності скористаємося геометричною інтерпретацією. Як елементарну подію розглядаємо Якщозмінюються в зазначених межах, томножинає квадратом зі стороною 1. Щоб визначити множину точок для подіїА, проведемо лініюНа рис. 2 подано множину, в якій заштриховано множину точок, що відповідають подіїА. Мірою кожної з розглядуваних множин є відповідна площа, тому

Рис. 1	Рис. 2