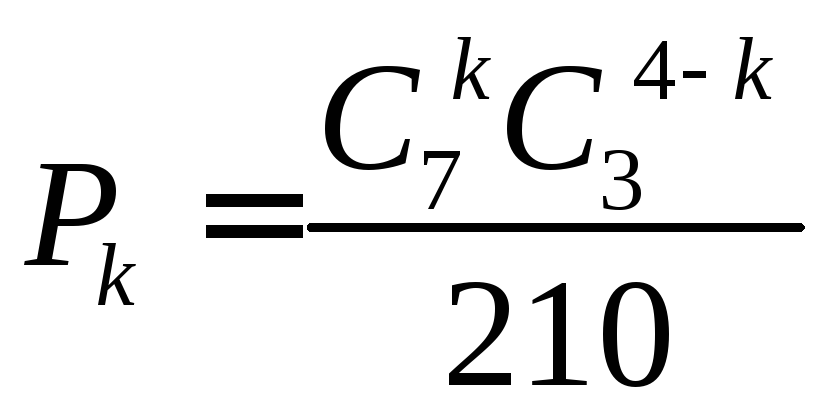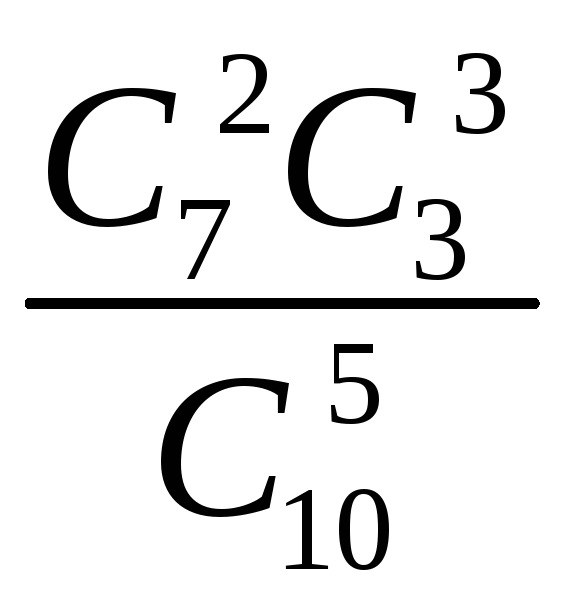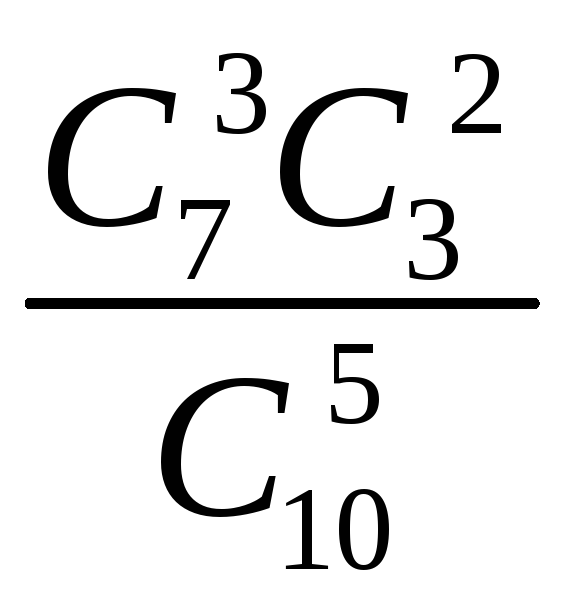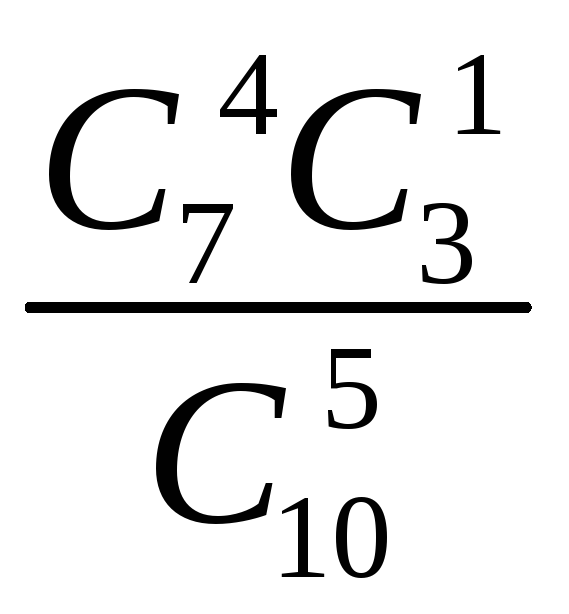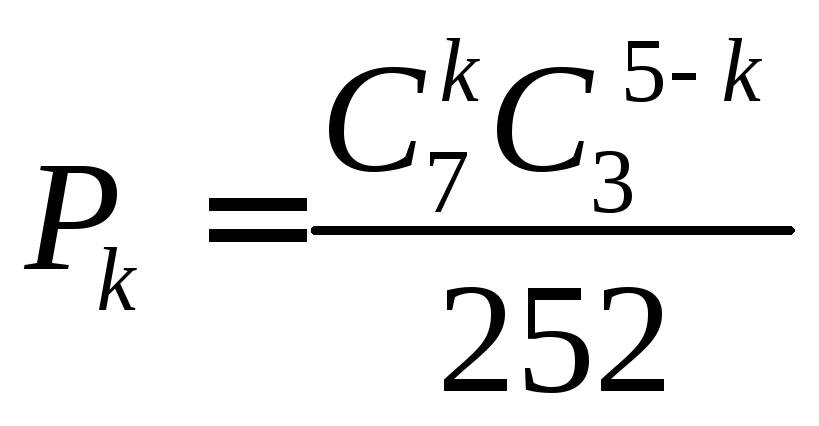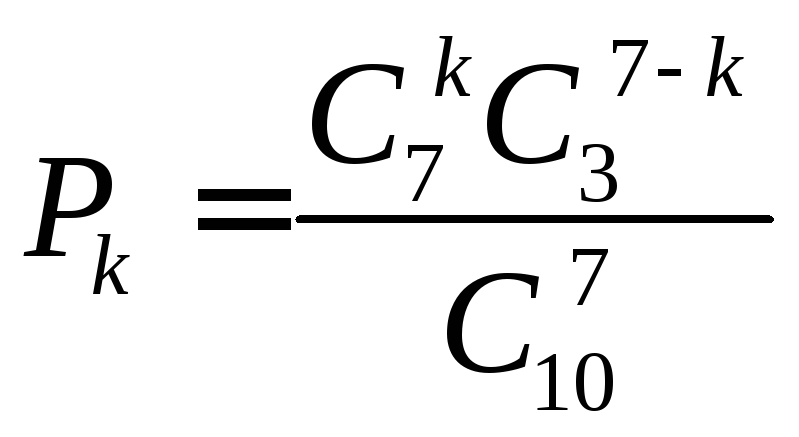Практичне заняття 8. Неперервна випадкова величина

Приклад.Неперервна випадкова величинаХмає закон розподілу ймовірностей у вигляді трикутника, зображеного на рис. 5.

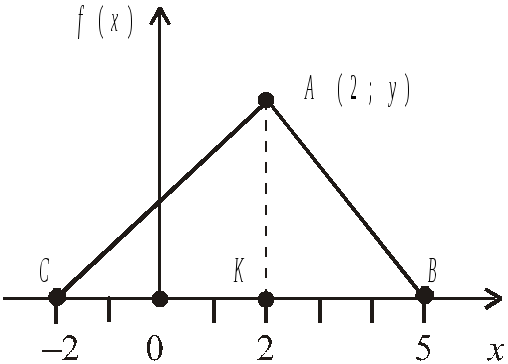
Рис. 5

Записати вирази для щільності ймовірностей і функції розподілу ймовірностей. Побудувати графік F(x) і обчислитиР(0 <X< 4).

Розв’язання.На проміжку [–2; 2] щільність ймовірностей змінюється за законом прямої пропорційної залежностіf(x) = k₁x + b₁(k₁ > 0), а на проміжку [2; 5] за аналогічним закономf(x) = k₂x + b₂(k₂ < 0). Для знаходження значень параметрівk₁,b₁, k₂, b₂обчислимо координати вершини цього трикутникаА(х,у). Абсциса цієї точки відома за умовою задачі:х= 2; ординату знаходимо за умовою нормування, згідно з якою площа цього трикутникаАВСмає дорівнювати одиниці:

Отже, шукані координати:

З

находимо рівняння прямої, яка проходить через точкиС (–2; 0) і:

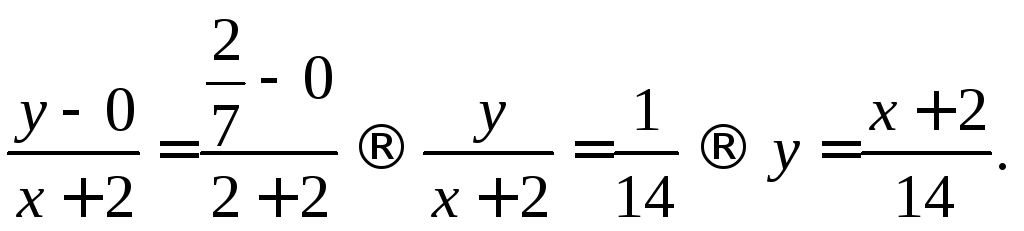
Отже, на проміжку [–2; 2] маємо:

Рівняння прямої, що проходить через точки :

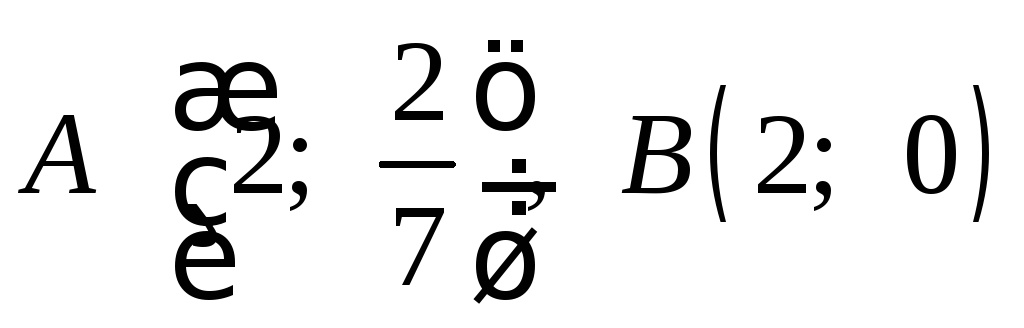Звідси на проміжку [2; 5] дістаємо:

Отже, на проміжку [–2; 5] щільність ймовірностей

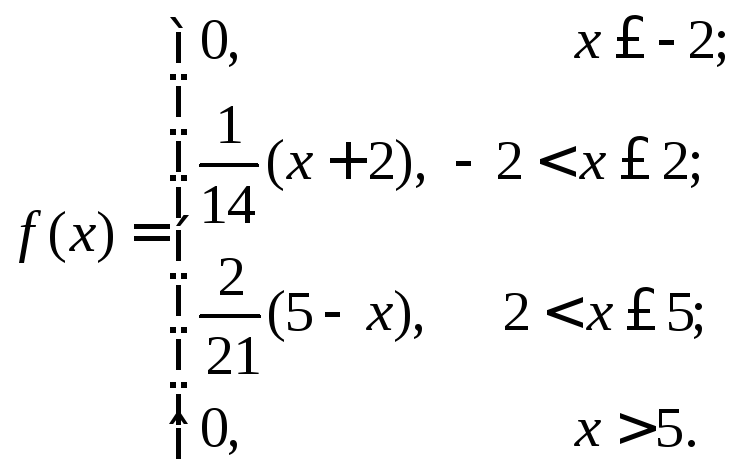
Знаходимо F(x) на обох розглядуваних проміжках:

1) на проміжку [–2; 2]:

2) на проміжку [–2; 5]:

Отже, функція розподілу ймовірностей

Графік F(x) зображено на рис. 6.

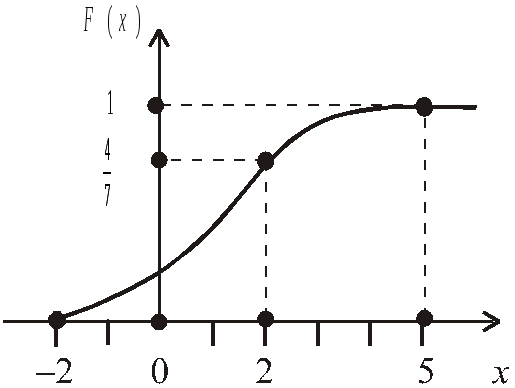
Рис. 6

Обчислюємо ймовірність події 0 < X< 4 згідно з (65) і (72).

На інтервалі [0; 4] діють два закони розподілу:

1)

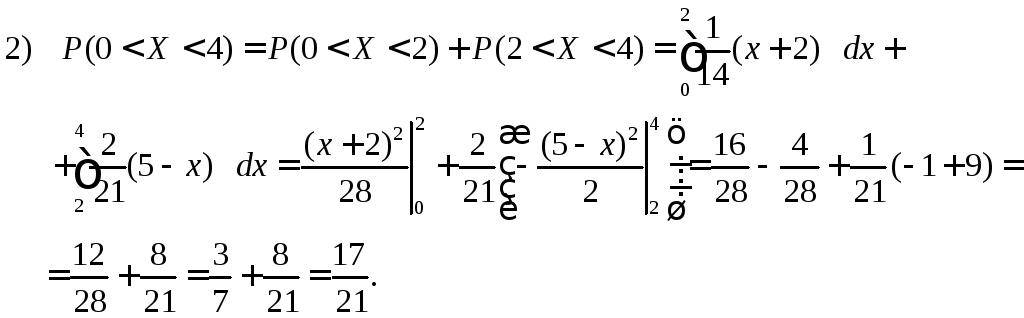
Отже, .

Приклад.Дано щільність ймовірностей

Обчислити М (Х).

Розв’язання.

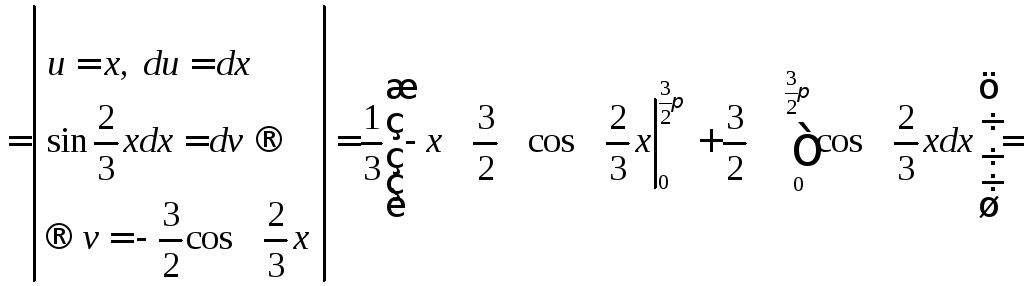
Приклад.За заданою функцією розподілу ймовірностей

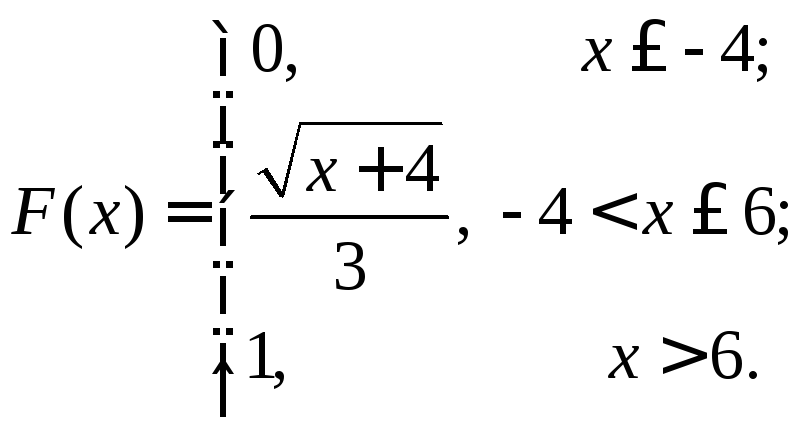
обчислити М(Х).

Розв’язання.Для обчисленняМ(Х) необхідно знайти щільність ймовірностей

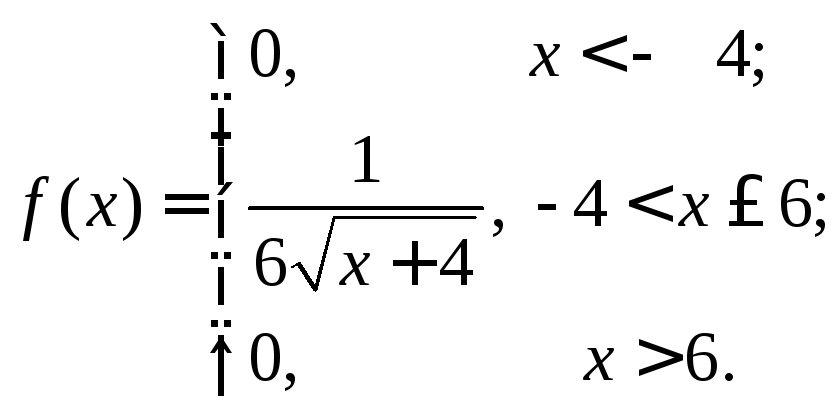
Тоді:

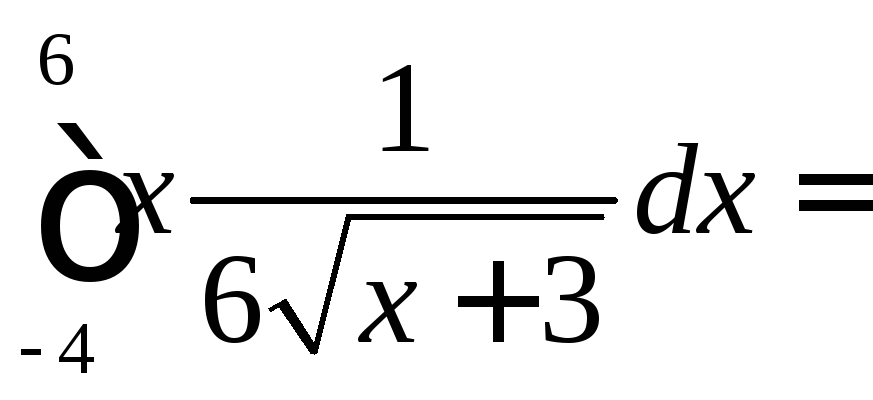
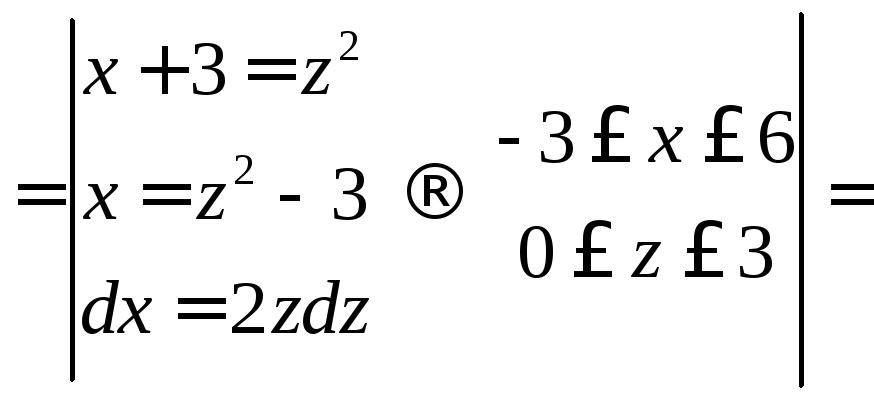
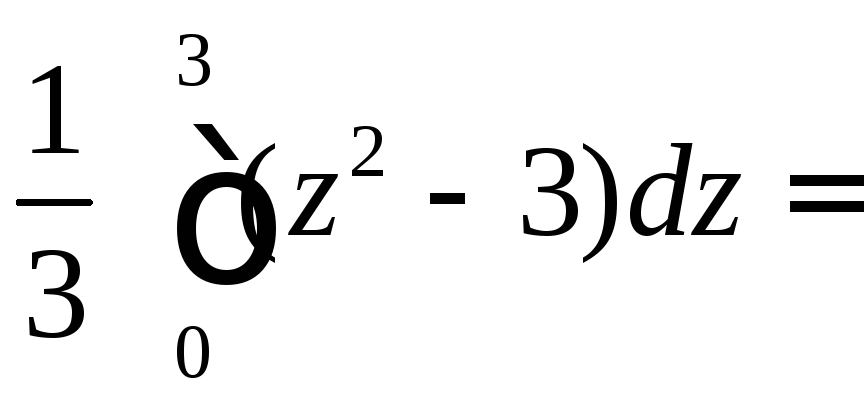
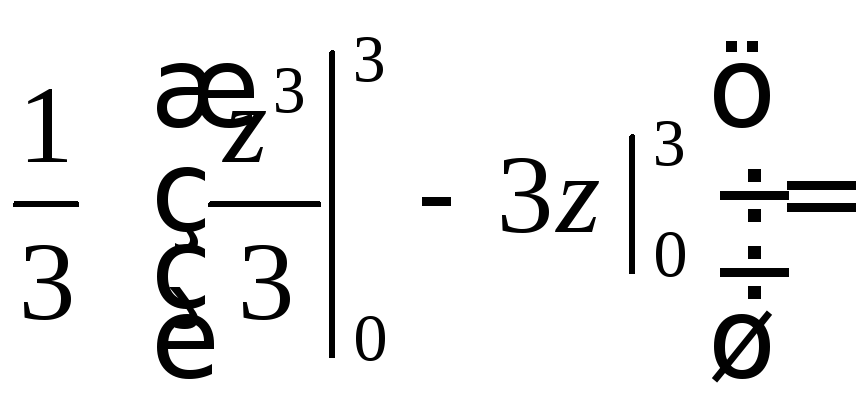
Практичне заняття 9. Неперервна випадкова величина

Приклад.Задано щільність імовірностей:

Обчислити D(X);(X). Знайти Мо; Ме.

Розв’язання.

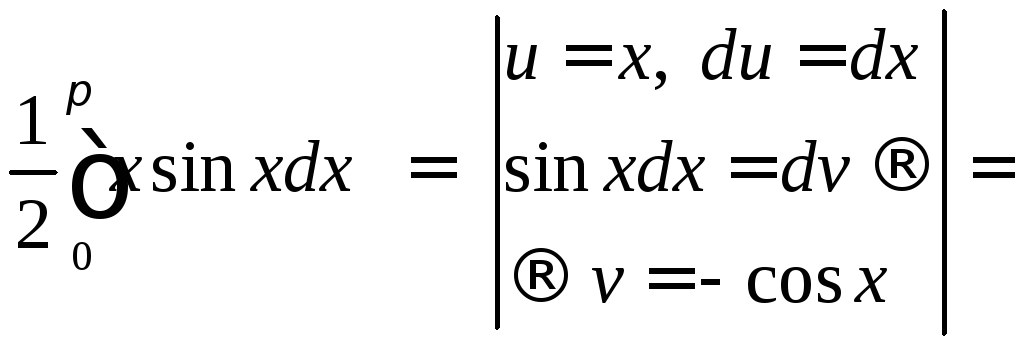
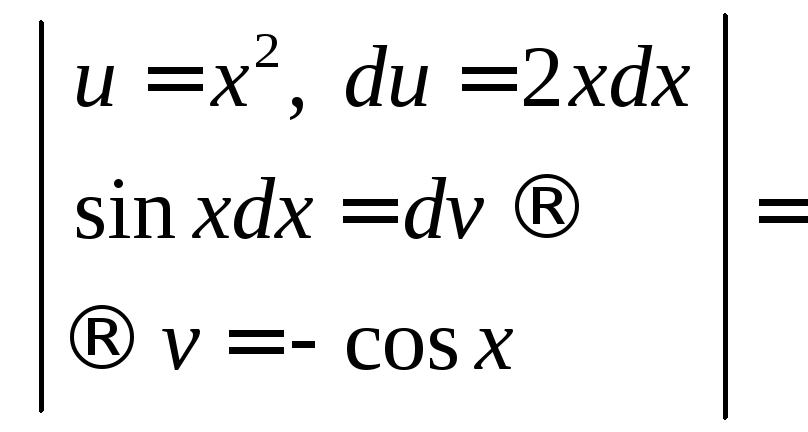
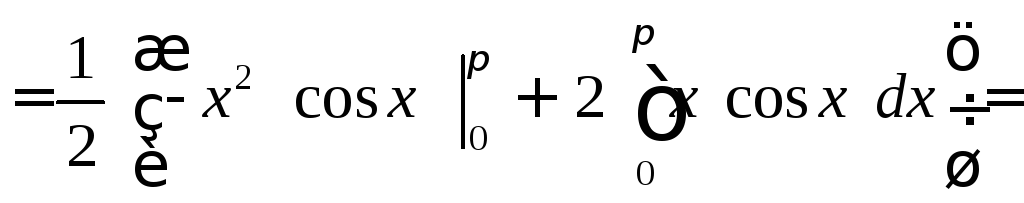
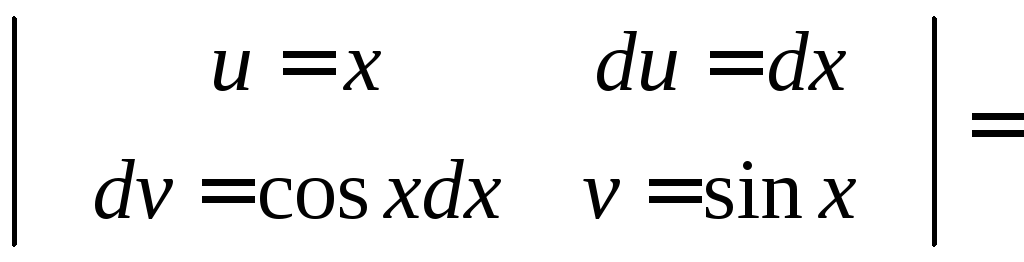
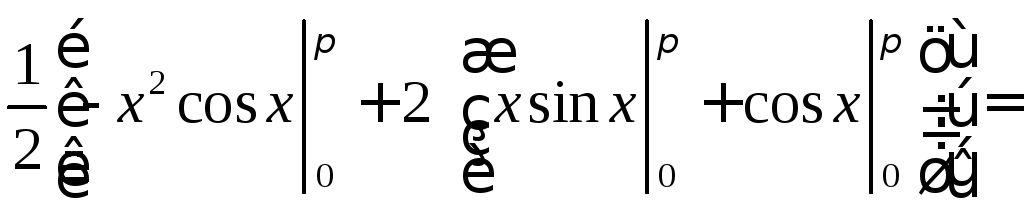
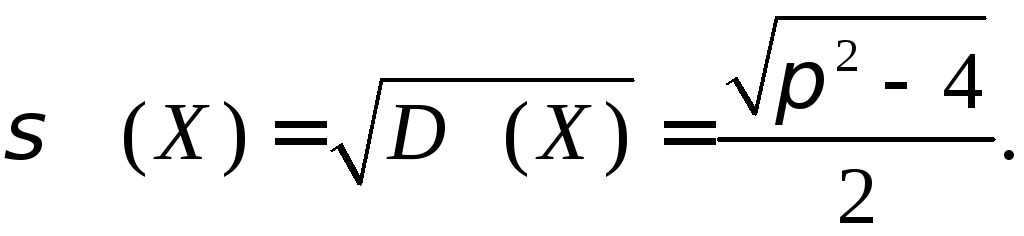
Графік f (x) зображено на рис. 7.

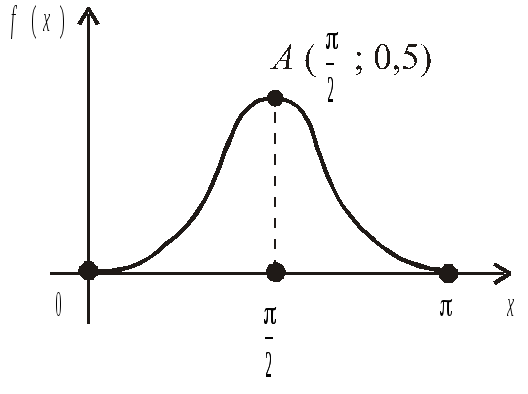
Рис. 7

Оскільки 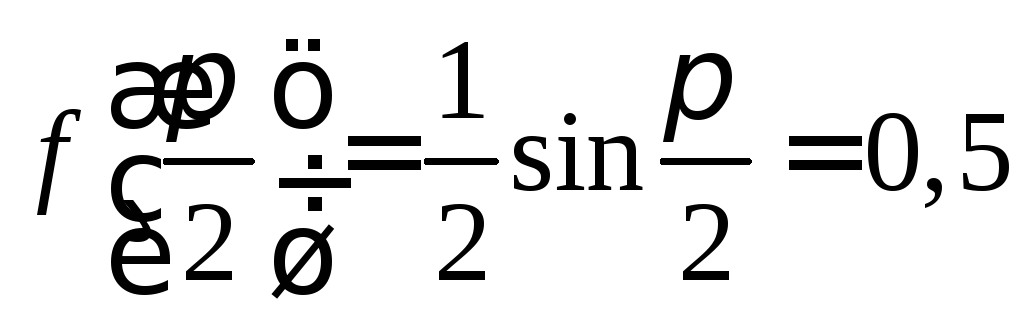є максимальним значенням, то

Знаходимо F(x) =

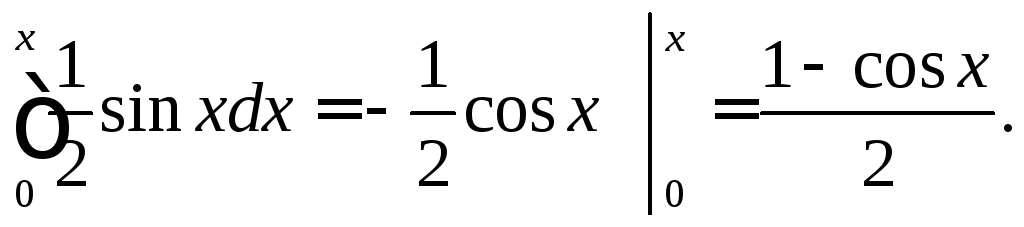
Отже,

.

Приклад.Задано щільність ймовірностей (рис 8).

Рис. 8

Обчислити D(X);(X); Mе. Знайти Мо.

Розв’язання.За умовою нормування знайдемо ординату точкиВ:

.

На проміжку [–2; 0] .

На [0; 4] .

Отже, щільність ймовірностей

Знаходимо функцію розподілу ймовірностей:

На проміжку [–2; 0]

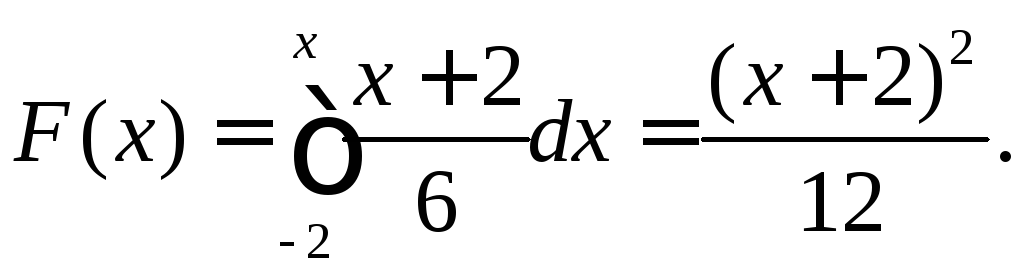
На [–2; 4]

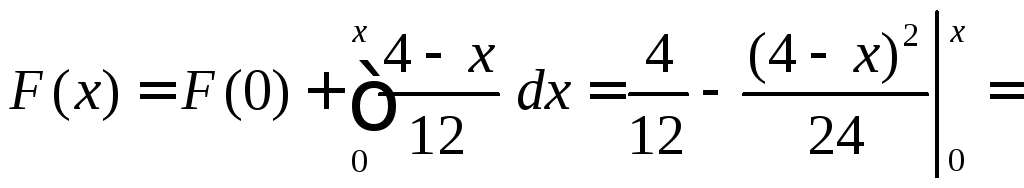
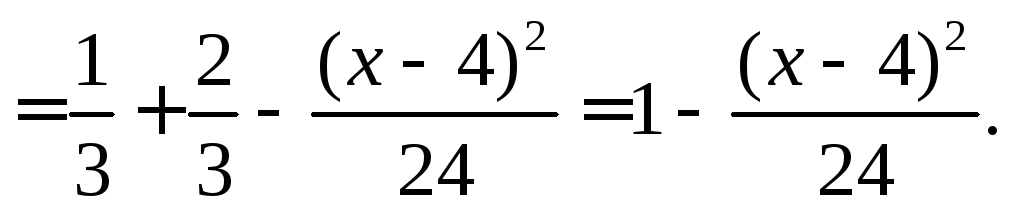
Отже, функцію розподілу ймовірностей можна подати у вигляді

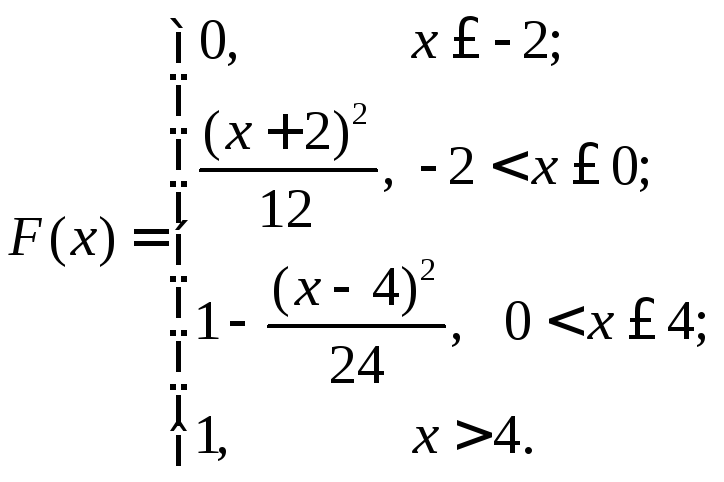
Графік F(x) зображено на рис. 9.

Рис. 9

Далі обчислюємо D(X):

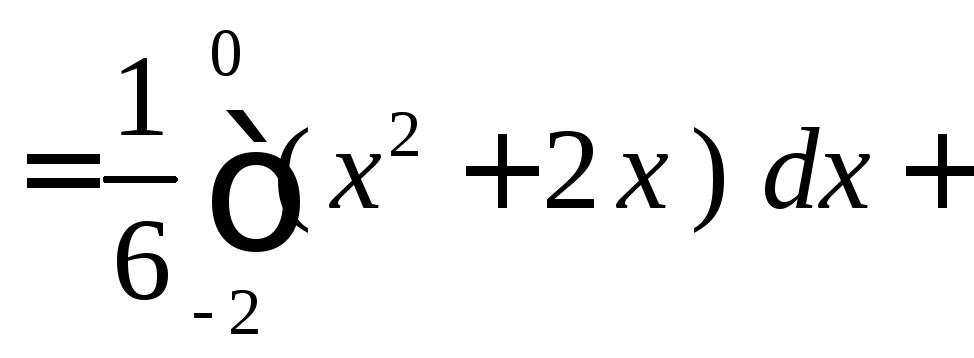
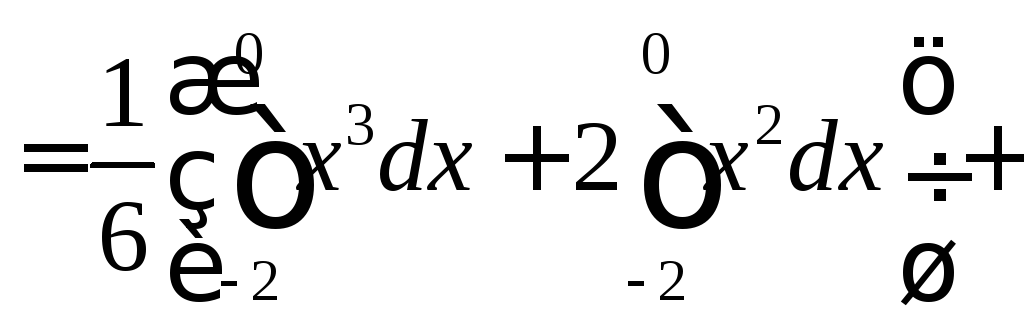
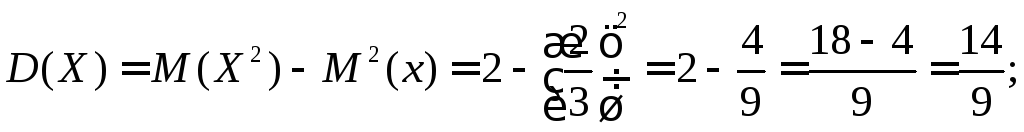
Для визначення Ме необхідно знайти проміжок, в якому вона міститься. Оскільки то медіана належить проміжку [0; 4].

Далі маємо:

Отже, Ме = Мо = 0.

Приклад.Задано щільність ймовірностей:

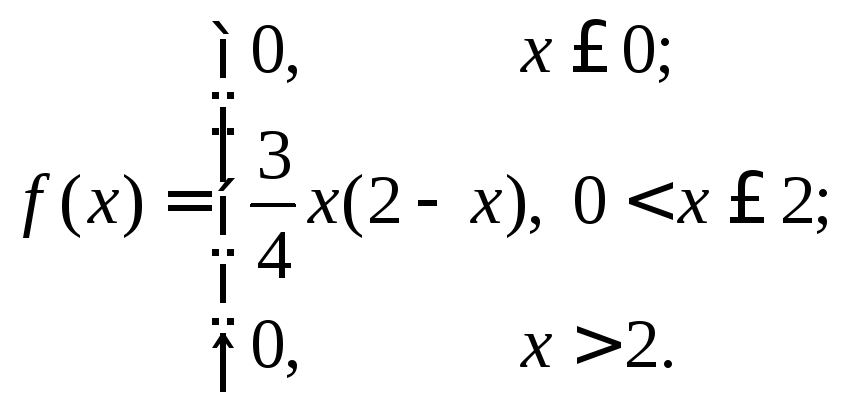
Обчислити Аs,Еs.

Розв’язання.

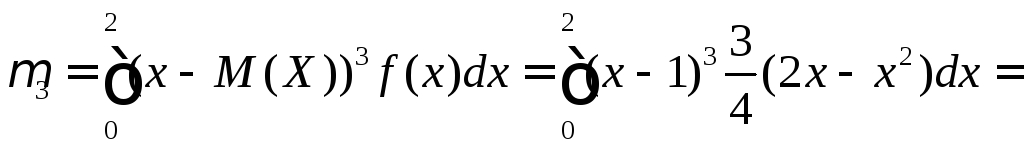
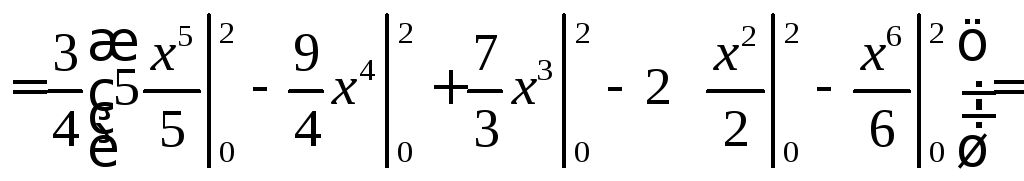
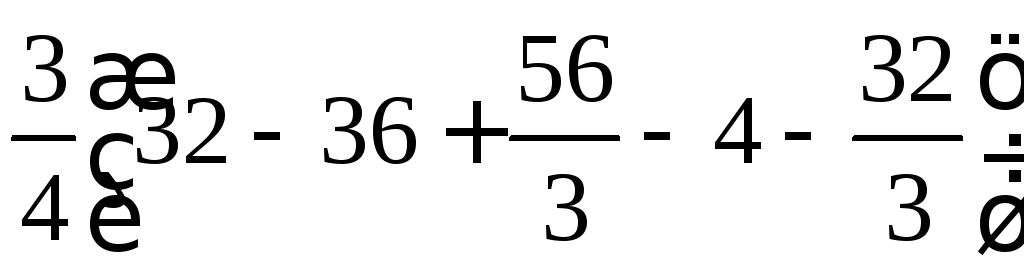
Оскільки ₃= 0, то іАs= 0. Отже, можливі значення випадкової величиниХсиметрично розподілені відносноМ(Х) = 1. Для обчисленняЕsнеобхідно знайти₄і.

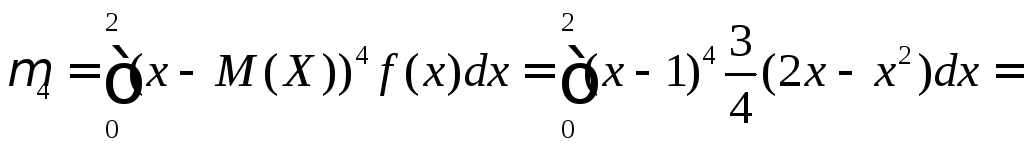
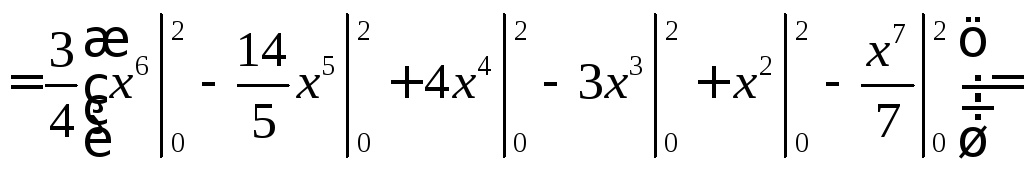
Практичне заняття 10. Закони розподілу дискретної випадкової величини

1. Біноміальний закон розподілу. Числові характеристики.

2. Закон розподілу Пуассона. Числові характеристики.

3. Геометричний розподіл.

4. Гіпергеометричний розподіл.

Приклад. У кожному із 100 контейнерів міститься по 8 виробів першого сорту, а решта 2 – браковані. Із кожного контейнера навмання беруть по одному виробу. Визначити М (Х),D (X),  (X) для дискретної випадкової величини Х – поява числа виробів першого сорту серед 100 навмання взятих.

Розв’язання. Цілочислова випадкова величинаХмає біноміальний закон розподілу. Із умови задачі маємо:

n = 100,p = 0,8,q = 0,2,k = 0, 1, 2, 3, ..., 100.

За формулами (235), (236), (237) дістаємо:

= 100 0,8 = 80;

= 100 0,80,2 = 16;

=4.

Приклад. У деякому населеному пункті маємо 0,1% дальтоніків. Навмання вибирають 5000 мешканців цього населеного пункту. ВизначитиМ(Х),D (X),(Х) випадкової величиниХ– числа дальтоніків, яких буде виявлено серед 5000 навмання вибраних мешканців.

Розв’язання. Цілочислова випадкова величинаХмає пуассонівський закон розподілу. Із умови задачі:n= 5000,p= 0,0001. Згідно з (10), (11), (12), дістаємо:

= 5000 0,0001 = 0,5;

= 0,5;

.

Приклад.Спортсмен стріляє зі спортивної рушниці по одній і тій самій мішені. Імовірність влучити в мішень при одному пострілі є величиною сталою і дорівнює 0,8. Стрільба по мішені ведеться до першого влучення. ВизначитиМ(Х),D(X),(Х) випадкової величиниХ– числа витрачених спортсменом набоїв.

Розв’язання. Випадкова величина Хє цілочисловою, з геометричним законом розподілу ймовірностей. За умовою задачі:p= 0,8;q = 0,2.

Згідно з (15), (16) і (17) маємо:

; ;.

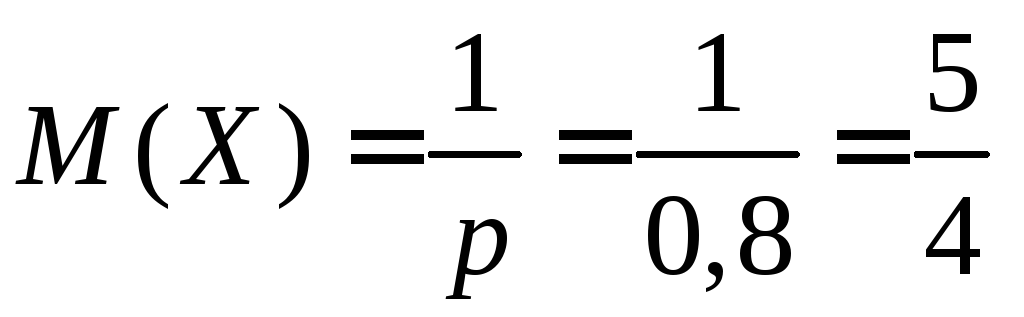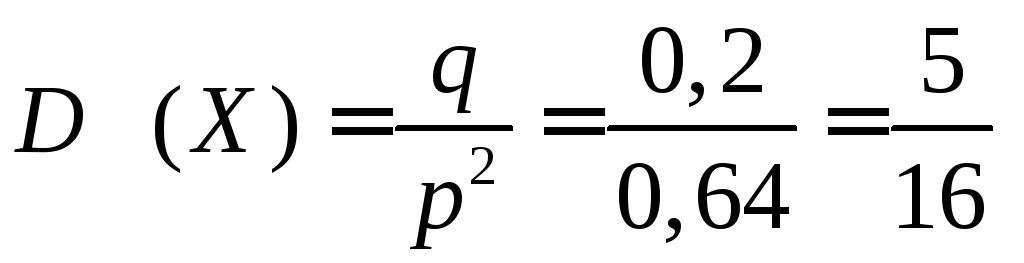Приклад.В ящику міститься 10 однотипних деталей, із них 7 стандартних, а решта є бракованими. Навмання із ящика берутьmдеталей. Побудувати закони розподілу цілочислової випадкової величиниХ —появу числа стандартних деталей середmнавмання взятих і обчислитиМ(Х),D(X),(Х), якщо 1)m = 4; 2)m = 5; 3)m = 7.

1). m = 4;= 7;= 3;k = 1, 2, 3, 4.

У табличній формі закон розподілу подається так:

	1	2	3	4

або

k	1	2	3	4

.

1.

;

2.

;

3. .

2) m = 5;n₁ = 7;n = 3;k = 2, 3, 4, 5.

У табличній формі закон подається так:

	2	3	4	5

або

k	2	3	4	5

1.  

;

2.  

;

.

3  .

3). m = 7;= 7;= 3;k = 4, 5, 6, 7.

У табличній формі закон подається так:

	4	5	6	7

або

k	4	5	6	7

.

1. ;

2. ;

3. .