Практичне заняття 11. Закони розподілу неперервної випадкової величини

1. Рівномірний закон розподілу. Числові характеристики.

2. Показниковий (експоненціальний) закон розподілу. Числові характеристики.

Задача. Випадкова величина X має функцію розподілу

Знайти параметр а, аналітичний вираз для щільності, імовірність потрапляння випадкової величини X в інтервал (–2; 5).

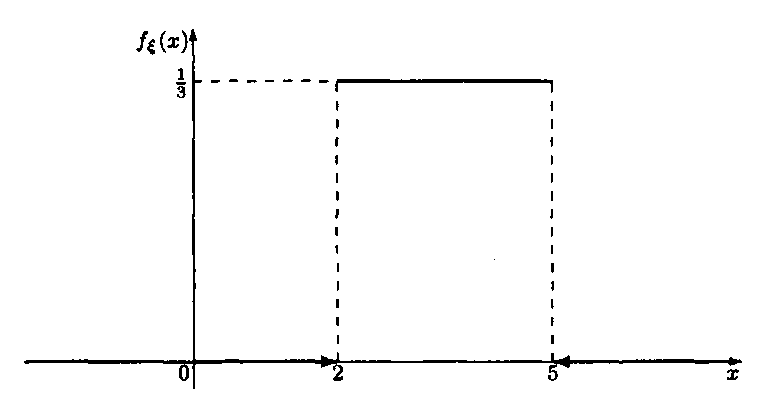
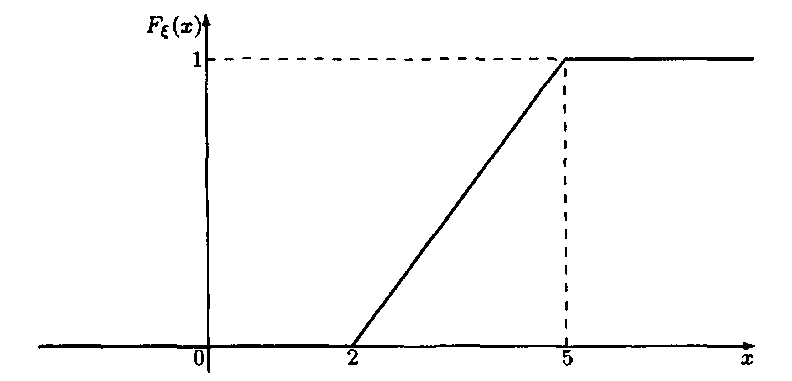
Задача. Випадкова величина має рівномірний закон розподілу на відрізку [2; 5]. Знайти аналітичні вирази для щільності та функції розподілу цієї випадкової величини. Побудувати їх графіки. Знайти ймовірність потрапляння випадкової величини в інтервал (0;3].

Задача. Поїзди метро йдуть з інтервалом 2 хв. Вважаючи, що часочікування поїзда на зупинці має рівномірний розподіл, знайти аналітичні вирази для щільності та функції розподілу цієї випадкової величини. Побудувати їх графіки. Знайти ймовірність того, що час очікування перевищуватиме 30 с.

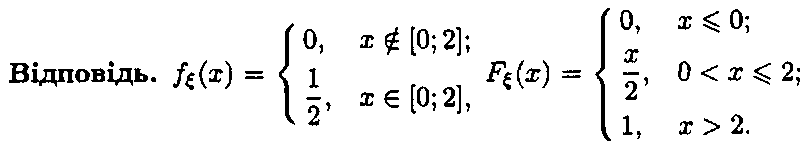
Задача. Випадкова величинаХрозподілена рівномірно. Знайти щільність її розподілу, якщо

Розв’язання. Щільність рівномірного розподілуОтже, потрібно визначити область зміни випадкової величини. Складаємо систему рівнянь:

Задача. Випадкова величина розподілена показниково зпараметром а. При якому значенні параметра ймовірність потрапляння випадкової величини на відрізокбуде найбільшою?

Розв’язання. Нехай параметра– неперервна й диференційована величина. Знайдемо ймовірність потрапляння випадкової величини на відрізок і дослідимо здобуту функцію на екстремум:

Покажемо, що при даному значенні адосягається максимум. Знайдемо другу похідну:

оскільки Друга похідна у критичній точці від’ємна, томув ній досягає максимуму.

Задача. Випадкова величина має показниковий розподіл з параметром= 3. Знайти ймовірність того, що випадкова величинанабуде значення з проміжку, якщо:

Задача. Випадкова величина має експоненціальний розподіл. Імовірність того, що ця випадкова величина набуде значення з проміжку [0; 5], дорівнює 0,7. Знайти ймовірність того, що ця випадкова величина набуде значення з проміжку [7; 9].

Практичне заняття. 12. Нормально розподілена випадкова величина

Приклад.Відомо, що випадкова величинаХмає закон розподілу.

Записати вирази для f (x), F(x) і накреслити їх графіки. Обчислити ,.

Розв’язання.

Графіки f (x), F(x) наведені на рис. 97 і 98.

Рис. 97 Рис. 98

1)

2)

Приклад. Зважування відбувається без систематичних (одного знака) похибок. Випадкові похибки зважування підкоряються нормальному закону з середнім квадратичним відхиленням 10 г. Обчислити ймовірність, що зважування буде проведене з похибкою, яка не перевищує 5 г.

Розв’язання. Використаємо формулу для знаходження ймовірності відхилення нормально розподіленої випадкової величини від її середнього значення

.

.

знайдено з таблиці значень функції Лапласа .

Відповідь: .

Приклад. Середній діаметр стовбурів дерев дорівнює 55 см, середнє квадратичне відхилення дорівнює 7 см. Вважаючи діаметр стовбура випадковою величиною, розподіленою нормально, знайти процент дерев, які мають діаметр менше 50 см.

Розв’язання. Використаємо формулу для знаходження ймовірності попадання нормально розподіленої випадкової величини у проміжок:

,

де – функція Лапласа,та– відповідно математичне сподівання і дисперсія випадкової величини.

Маємо, ,,,.

= .

Отже, процент дерев, які мають діаметр менше 50 см .

Відповідь: .

Приклад. Виріб вважається відмінної якості, якщо відхилення його розмірів від номіналу не перевищує за абсолютною величиною 3,5 мм. Випадкові відхилення розмірів від номіналу підкоряються нормальному закону з середнім квадратичним відхиленням 2 мм і відсутні систематичні відхилення одного знака. Який відсоток виробів відмінної якості серед виготовлених?

Розв’язання. Використаємо формулу для знаходження ймовірності відхилення нормально розподіленої випадкової величини від її середнього значення

.

.

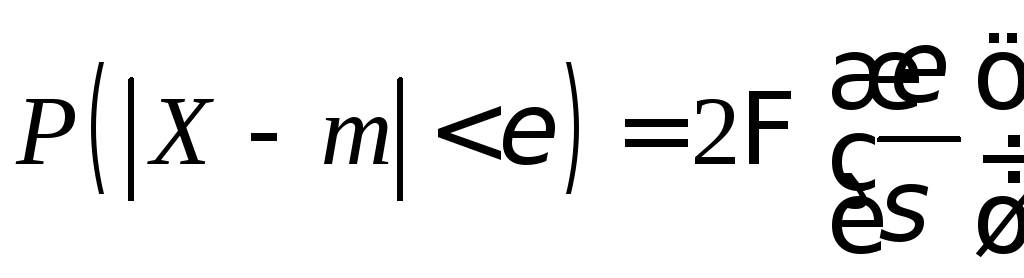знайдено з таблиці значень функції Лапласа .

Отже, вироби відмінної якості складають %.

Відповідь:%.