Практичне заняття 3. Формула повної ймовірності. Формула бейєса

1. Формула повної ймовірності.

2. Формула Бейєса

Задача. На двох верстатах-автоматах виробляють однакові деталі, які надходять на транспортер. Продуктивність першого верстата утричі більша, ніж другого, причому перший верстат виробляє нестандартну деталь з імовірністю 0,15, а другий – з імовірністю 0,2. Знайти ймовірність того, що навмання взята з транспортера деталь буде стандартною.

Розв’язання.Розглянемо події:А–«вибрана деталь стандартна»;– «деталь виготовлено напершому верстаті»; – «деталь виготовлено на другому верстаті». Подіїі несумісні й утворюють повну групу, що ж до подіїА, то вона може відбутись одночасно з кожною із цих подій. Умовні ймовірності настання події А відомі. Згідно з умовою, що продуктивність першого верстата утричі більша, ніж другого, знаходимоЗа формулою повної ймовірності маємо:

Задача. Партію виготовлених деталей перевіряли два контролери. Перший перевірив 45 %, а другий – 55 % деталей. Імовірність припуститися помилки під час перевірки для першого контролера становить 0,15, для другого – 0,1. Після додаткової перевірки в партії прийнятих деталей виявлено браковану. Оцінити ймовірність помилки для кожного контролера.

Розв’язання.Розглянемо події:А– «виявлено браковану деталь».– «деталь перевіряв перший контролер»; – «деталь перевіряв другий контролер»; Подіїі несумісні й утворюють повну групу. ПодіяАвідбулась одночасно з однією із цих подій, імовірності яких потрібно переоцінити. Застосуємо формулу Байєса.

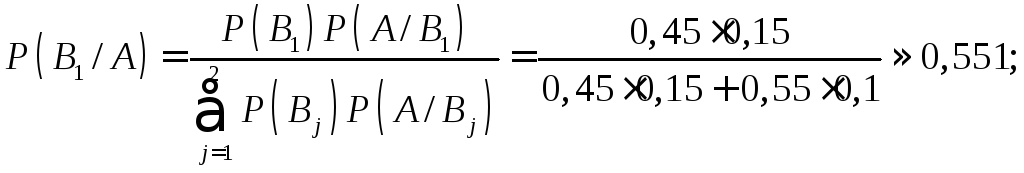
Отже, більш імовірно, що помилки припустився перший контролер.

Задача. Маємо дві партії однакових виробів. Перша складається з 15 стандартних і 4 нестандартних, друга – із 18 стандартних і 5 нестандартних виробів. Із навмання вибраної партії взято один виріб, який виявився стандартним. Знайти ймовірність того, що другий навмання взятий виріб також буде стандартним.

Розв’язання.Розглянемо події:– «перший виріб взято з першої партії»;– «перший виріб узято з другої партії»;А– «перший узятий виріб стандартний»;С– «другий узятий виріб стандартний». За формулою повної ймовірності знаходимо ймовірність подіїА:

За формулою Байєса обчислюємо умовні ймовірності і

Імовірність події Сзнаходимо за формулою:

Умовні ймовірності такі:

Отже,

Задача.Деталь може надійти для обробки на перший верстат із імовірністю 0,2, на другий верстат – із імовірністю 0,3 і на третій – із імовірністю 0,5. При обробці деталі на першому верстаті ймовірність допустити брак дорівнює 0,01, на другому і третьому верстатах ця ймовірність відповідно дорівнює 0,05 і 0,08. Оброблені деталі вміщують в одну шухляду. Навмання взята звідти деталь виявилась бракованою. Яка ймовірність того, що її обробляв перший верстат?

Відповідь..

Задача.Клапани, виготовлені цехом заводу, перевіряють три контролери. Імовірність того, що клапан потрапить на перевірку до першого контролера дорівнює 0,3, до другого – 0,5 і до третього – 0,2. Імовірність того, що бракована деталь буде виявлена для першого, другого і третього контролерів відповідно дорівнює 0,95, 0,9, 0,85. Під час повторної перевірки відбракованої деталі вона виявилась бракованою. Яка ймовірність того, що цю деталь перевіряв третій контролер?

Відповідь. .