Практичне заняття 21. Елементи теорії кореляції

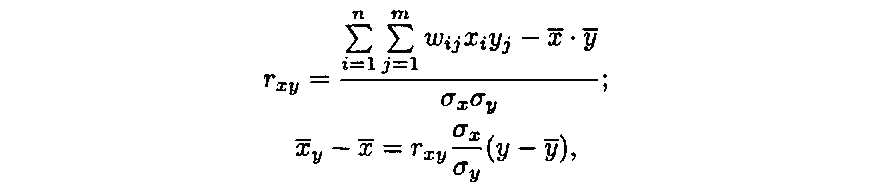
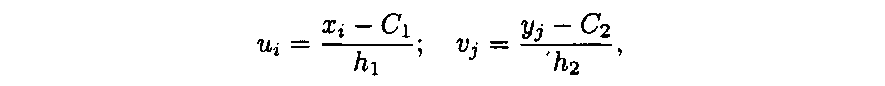
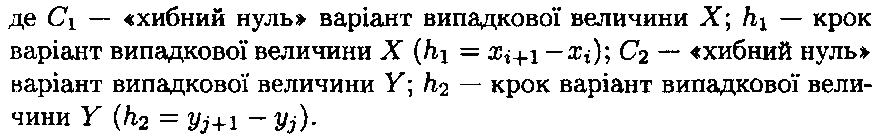
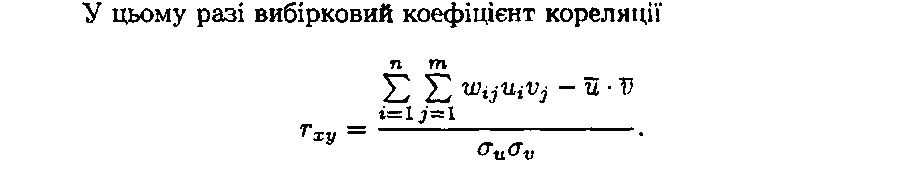
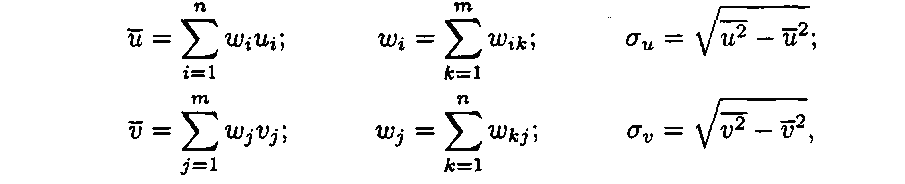
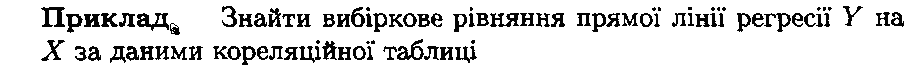
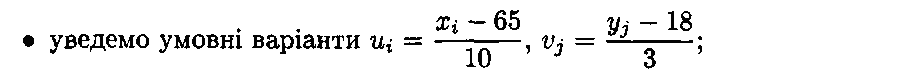
Маємо таблицю

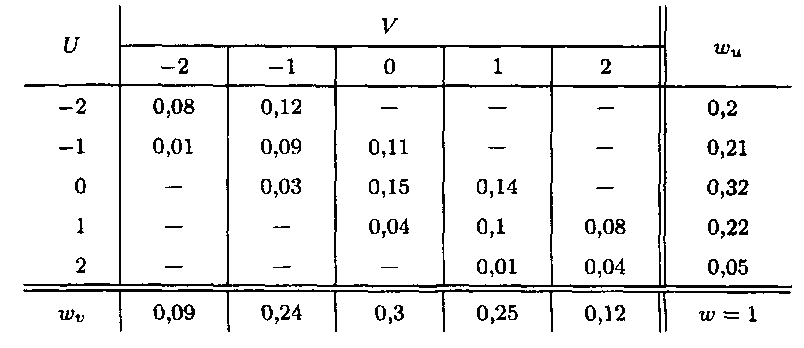
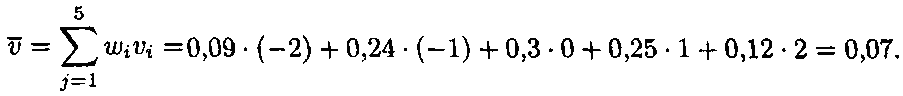
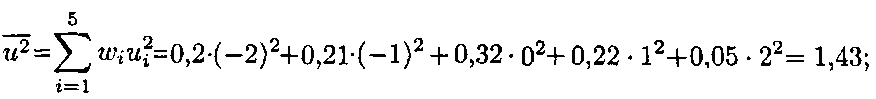
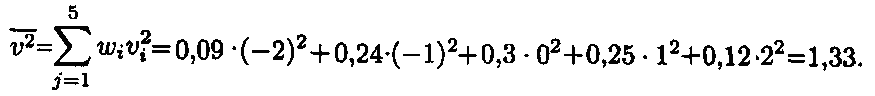
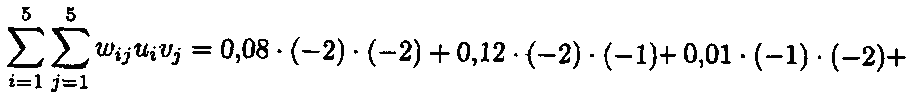
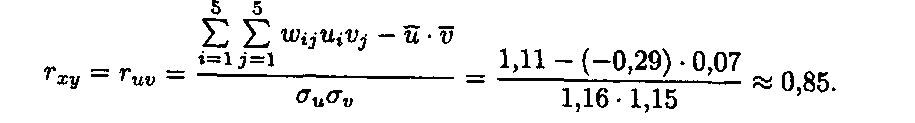
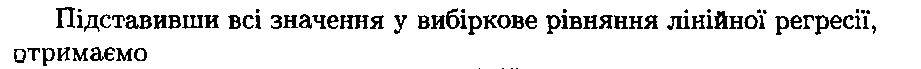
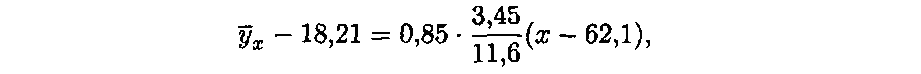
Практичне заняття 22. Випадкові процеси

Задача. Знайти: а) математичне сподівання; б) кореляційну функцію; в) дисперсію випадкової функції, де– випадкова величина, причому,.

Розв’язання. а) Знайдемо шукане математичне сподівання (невипадковий множниквинесемо за знак математичного сподівання):

.

б) Знайдемо центровану функцію:

.

Знайдемо шукану кореляційну функцію:

.

Враховуючи, що , маємо

.

в) знайдемо дисперсію для чого покладемо

.

Задача. Знайти характеристики випадкової функції, якщо,.

Розв’язання. Знайдемо,,.

.

Отже, .

Задача. Даноз характеристиками:,. Знайти характеристики,,, якщо.

Розв’язання. .

.

.

Практичне заняття 23. Моделювання випадкових величин методом монте-карло

Задача. Розіграти шість можливих значень дискретної випадкової величини, закон розподілу якої задано у вигляді таблиці:

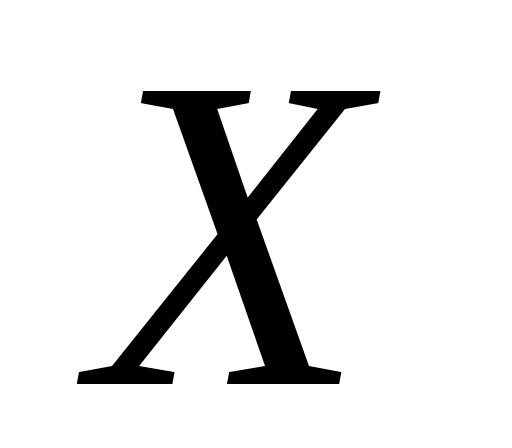
	2	10	18
	0,22	0,17	0,61

Розв’язання. Розіб’ємо інтервалосіточками з координатами 0,22; 0,22+0,17=0,39 на три інтервали,,.

Випишемо з таблиці рівномірно розподілених випадкових чисел шість випадкових чисел, наприклад 0,32; 0,17; 0,90; 0,05; 0,97; 0,87.

Випадкове число належить частковому інтервалу, тому дискретна випадкова величина, що розігрується, набула можливого значення.

Аналогічно одержуємо решту можливих значень.

Отже, маємо розіграні можливі значення: 10; 2; 18; 2; 18; 18.

Задача. Розіграти п’ять дослідів за схемою Бернуллі: дослід складається з трьох незалежних випробувань, в кожному з яких ймовірність появи подіїрівна 0,4.

Вказівка. а) Скласти спочатку закон розподілу дискретної випадкової величини– число появ подіїу трьох незалежних випробуваннях; б) взяти для визначеності випадкові числа 0,945; 0,572; 0,857; 0,367; 0,897.

Задача. Дано ймовірності трьох подій, що утворюють повну групу подій:,,:,,. Розіграти п’ять випробувань, в кожному з яких з’являється одна з трьох подій, що розглядається.

Розв’язання .Необхідно розіграти дискретну випадкову величинуз законом розподілу:

	0,22	0,31	0,47

Розіб’ємо інтервал на три інтервали,,.

Випишемо з таблиці рівномірно розподілених випадкових чисел п’ять випадкових чисел, наприклад 0,61; 0,19; 0,69; 0,04; 0,46.

Розглянувши послідовно належність випадкових чисел інтервалам отримуємо послідовність подій: ,,,,.

Задача. Подіїінезалежні і сумісні. Розіграти чотири випробування, в кожному з яких ймовірність появи подіїрівна 0,7, а події– 0,4.

Розв’язання. Можливі чотири результати випробування:

;

;

;

.

Задача зведена до розігрування повної групи подій, що в свою чергу зводиться до розігрування дискретної випадкової величини з законом розподілу:

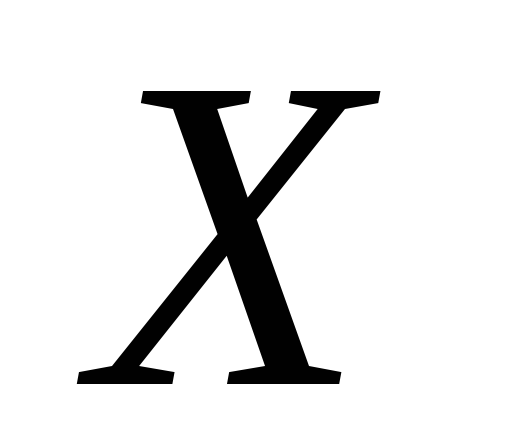
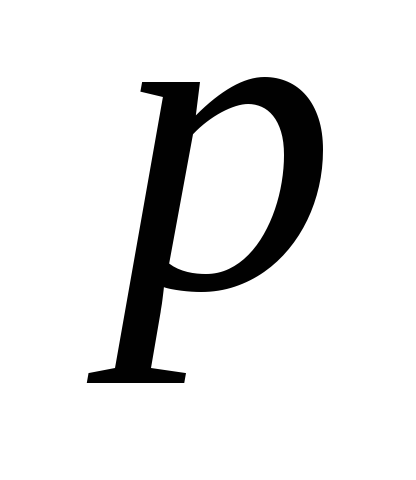
	0,28	0,42	0,12	0,18

Випишемо з таблиці рівномірно розподілених випадкових чисел чотири випадкових числа, наприклад 0,32; 0,17; 0,90; 0,05.

Аналогічно до попередньої задачі знаходимо шукану послідовність результатів чотирьох випробувань: ,,,.