2.1 Решение задачи в средеDelphi
Ниже представлен блок-схема разработанного алгоритма (рис.2.1.1).
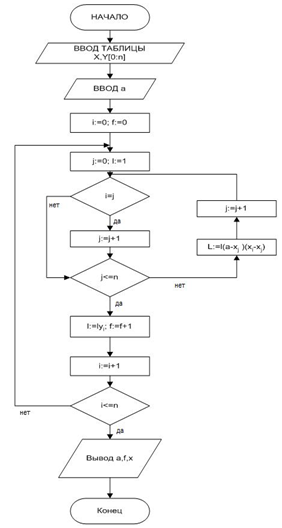
Рисунок 2.1.1- Блок-схема алгоритма
В данной курсовой работе интерфейс программы в Delphi имеет вид (рис 2.1.2):
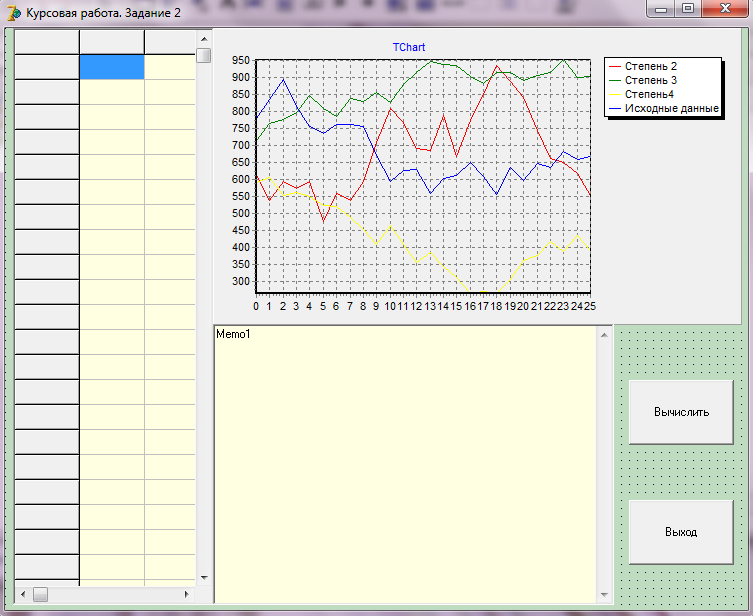
Рисунок 2.1.2- Интерфейс программы
Вычисление производится путем нажатия кнопки "Вычислить"
(рис. 2.1.3 ):
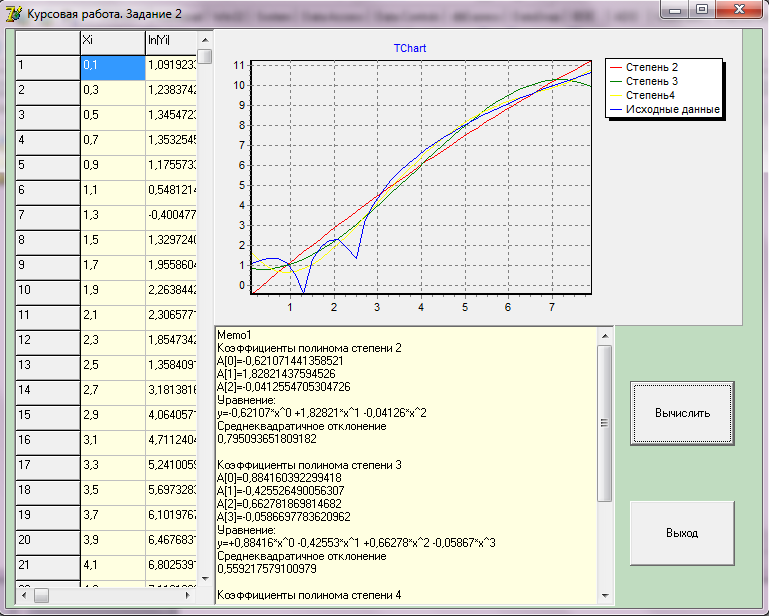
Рисунок 2.1.3
Код разработанной программы представлен ПРИЛОЖЕНИИ Б.
2.2 Решение задачи в среде mathcad
2.2.1 Находжение полинома 2,3,4 степеней и среднеквадратичные отклонения
Ниже представлено находжение полинома 2, 3 и 4 степени (рис.2.1.4).
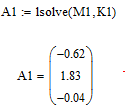
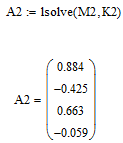
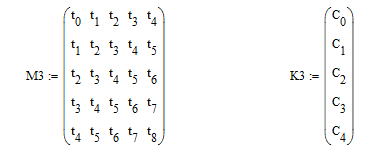
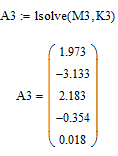
Рисунок 2.1.4
Вычисляем среднеквадратичные отклонения (рис. 2.1.5)
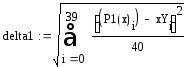
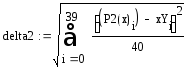
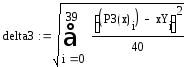
Полностью расчеты представлены в ПРИЛОЖЕНИЕ В.
3 Вывод. Результаты
В ходе работы был проведен сравнительных анализ полученных результатов с помощью сред Delphi и МathCad (таб. 3.1, 3.2, 3.3).
Таблица 3.1 - Коэффициенты полинома степени 2
|
Номер коэффициента |
Delphi |
MathCad |
|
A[0] |
-0,621071441358521 |
-0,62 |
|
A[1] |
1,82821437594526 |
1,83 |
|
A[2] |
-0,0412554705304726 |
-0,04 |
|
Среднеквадратичное отклонение |
-0,0586697783620962 |
0,79503137 |
Таблица 3.2 - Коэффициенты полинома степени 3
|
Номер коэффициента |
Delphi |
MathCad |
|
A[0] |
0,884160392299418 |
0,884 |
|
A[1] |
0,425526490056307 |
-0,425 |
|
A[2] |
0,662781869814682 |
0,663 |
|
A[3] |
-0,058669778362096 |
-0,059 |
|
Среднеквадратичное отклонение |
0,559217579100979 |
0,55924813 |
Таблица 3.3 - Коэффициенты полинома степени 4
|
Номер коэффициента |
Delphi |
MathCad |
|
A[0] |
1,97344464646087 |
1,973 |
|
A[1] |
-3,13311206518657 |
-3,133 |
|
A[2] |
2,18339747827071 |
2,183 |
|
A[3] |
-0,354211631253284 |
-0,354 |
|
A[4] |
0,0184713658056992 |
0,018 |
|
Среднеквадратичное отклонение |
0,430514664241794 |
0,430534574 |
Заключение
В ходе выполнения курсовой работы были выполнены все поставленные задачи. Освоены навыки разработки приложений, что позволит использовать полученные знания на практике. Получены знания по теме нелинейные уравнения и аппроксимация табулированных функций. Рассмотрены и изучены методы отделения корней, методы решения нелинейных уравнений и метод наименьших квадратов.
В ходе разработки первого задания курсовой работы, используя базу полученных знаний, был проведен математический анализ заданной функции. На базе проведенного анализа были получены данные характеризующие заданную функцию. В программе Mathcad были построены графики заданной функции при различных значениях коэффициента а. Произведен подбор параметра а, вследствие которого было выбрано конкретное значение (а=0,2). Был определен интервал существования корня для заданной функции. На основе полученных данных исследования заданной функции, при коэффициенте а=0,2 было разработано приложение в среде Delphi. Приложение способно находить корни уравнения на заданном интервале их существования при помощи метода касательных, метода хорд и метода деление отрезка пополам.
В ходе разработки второго задания курсового проекта на тему: "Аппроксимация табулированных функций методом наименьших квадратов", получили результаты, которые выполнены с большой точностью, как в среде Delphi, так и в среде MathCad, которые удовлетворяют условию поставленной задачи.
За время выполнения проекта изучили методы аппроксимации, и научились оценивать полученные результаты. Полученные графики и значения в обеих средах практически одинаковы, что свидетельствует о правильности выполнения курсовой работы. Была замечена закономерность, что при увеличении степени многочлена среднеквадратичное отклонение уменьшается, а, следовательно, возрастает точность вычислений.
Разработанные приложения соответствуют требованиям заданий на курсовую работу. Исходные тексты программ, а так же исполняемые файлы представлены на диске.
В ходе выполнения курсовой работы получены как теоретические, так и практические навыки работы в среде разработки программ Delphi на алгоритмическом языке Object Pascal.
Также были углублены и закреплены знания по алгоритмизации, программированию и решению в интегрированной визуальной среде программирования Delphi задач по специальности.
Цель курсовой работы достигнута, задачи решены в полном требуемом объёме.