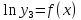2.2.3 Уточнение корней методом хорд

Решение поставленной задачи с использованием для уточнения кор-

ней метода хорд производится практически аналогично. Рекуррентное

соотношение для вычисления приближений корня по методу хорд име-

ет вид

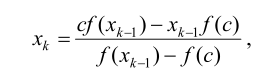
где с — значение конца отрезка, для которого выполняется условие

В качестве начального приближения выбирается конец отрезка, ос-

тавшийся после выбора с. То есть если с = a, то начальным приближе-

нием корня выбирают b и наоборот.

Блок-схема алгоритма уточнения корней этим методом отличается от уточнения корней методом касательных лишь списком вводимых исходных значений (блок 2) и рекуррентной формулой (блок 3).

Текст программы для уточнения корней заданного в условии задачи уравнения методом хорд, написанной на языке Pascal, может иметь следующий вид:

Program MetChord;

var c,x,e,M:real;

{Описание функции}

function f(x:real):real;

begin

f:=3*sin(sqrt(x))+x/15-1.8

end;

{Описание функции, реализующей алгоритм метода уточнения корней}

function MCh(c,x,e,M:real):real;

var x0:real;

begin

repeat

x0:=x;

x:=(c*f(x0)-x0*f(c))/(f(x0)-f(c));

until abs(f(x))/M<=e;

MCh:=x;

end;

{Раздел операторов}

13

begin

writeln('Введите исходные данные c, x, e, M');

readln(c,x,e,M);

{Находим с помощью функции МCh уточненное значение корня и присваиваем его переменной х}

x:=MCh(c,x,e,M);

writeln('Уточненное значение корня x=',x:7:4);

readln;

end.

2.2.4 Разработка программного продукта в среде Delphi

При разработке данной программы используются Form1 (главная форма), используется для выполнения основных функций программы.

Описание используемых компонентов:

1. Label –компонент на форме, который предоставляет не изменяемую текстовую информацию на форме;

2. Edit – стандартный управляющий элемент Windows для ввода. Используется для ввода и отображения данных;

3. Memo – компонент на форме, который предоставляет возможность вывода информации в ограниченной на форме области, виде строк текста;

4. Button – компонент, выполняющий функцию кнопок, при нажатии на которые выполняется заданное программой действие;

5. Chart – компонент предназначен для графического отображения числовых данных.

Внешний вид разработанного приложения представлен на рисунке 2.9.

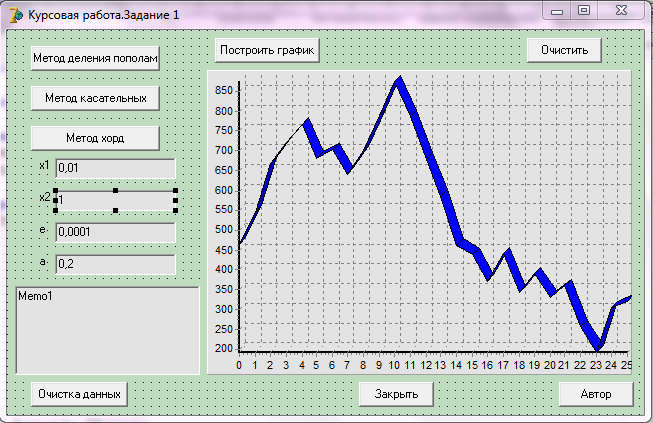
Рисунок 2.9 – Внешний вид разработанного приложения

Код, разработанного приложения, представлен в ПРИЛОЖЕНИИ А.

1. Результаты тестирования программного продукта

После нажатия на копку выбранного метода вызываются подпрограммы решения нелинейных уравнений, результаты которых помещаются в компоненты «TMemo». (рисунок 2.10)

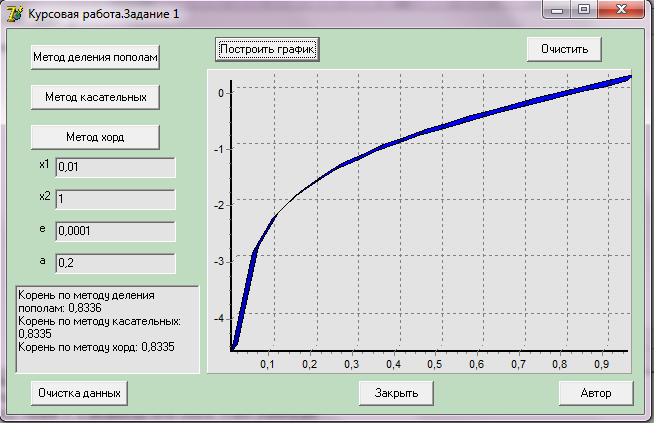
Рисунок 2.10 – Результат работы разработанного приложения

3 Вывод. Сравнение полученых результатов различными способами

В таблице 2.3.1 сведены решения, полученные различными методами

Таблица 2.3.1 – Данные, полученные различными методами

Метод решения	Параметр а	Корни уравнения
Деления пополам	0,2	0,8336
Касательных		0,8335
Хорд		0,8335
Средствами MathCad		0,8293

Задание 2

1 Постановка задачи

1. Разработать алгоритм нахождения коэффициентов трех аппроксимирующих полиномов (многочленов) вида

P_n(x)=A₀+A₁x+A₂x²+…+A_mxⁿ (2.1)

Для табулированной функции lny=f(x) в соответствии с данными таблицы 1.1. Построить блок-схему алгоритма. Создать программу на языке Pascal (Delphi), реализующую разработанный алгоритм.

2. Рассчитать среднеквадратичные отклонения для каждого из трех случаев по формуле:

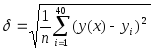(2.2)

3. Построить графики 3-х полученных приближающих функций в одной системе координат.

4. Решить задачу средствами MathCad.

Результаты решения задачи с помощью созданной программы и в среде MathCad нужно представить в виде построенных с помощью найденных коэффициентов трёх полиномов; таблицы, содержащей полученные с помощью найденных полиномов значения функции в точках х_i и среднеквадратичных отклонений.

Исходные данные

Ниже в таблицах представлены вариант(таблица 1.1) и исходные данные (таблица 1.2).

Таблица 1.1– Исходные данные

n	x	lny
1	0,1	1.091
2	0,3	1.238
3	0,5	1.345
4	0,7	1.353
5	0,9	1.176
6	1,1	0.548
7	1,3	-0.4
8	1,5	1.329
9	1,7	1.955
10	1,9	2.264
11	2,1	2.307
12	2,3	1.854
13	2,5	1.358
14	2,7	3.181
15	2,9	4.064
16	3,1	4.711
17	3,3	5.241
18	3,5	5.697
19	3,7	6.102
20	3,9	6.467
21	4,1	6.803
22	4,3	7.112
23	4,5	7.4
24	4,7	7.671
25	4,9	7.926
26	5,1	8.169
27	5,3	8.396
28	5,5	8.614

Продолжение таблицы 1.1

29	5,7	8.821
30	5,9	9.02
31	6,1	9.211
32	6,3	9.395
33	6,5	9.572
34	6,7	9.742
35	6,9	9.907
36	7,1	10.065
37	7,3	10.219
38	7,5	10.369
39	7,7	10.5136
40	7,9	10.654

Таблица 1.2 - Вариант задания

Вариант	Вид функции	Степень многочлена
22		2,3,4