
- •Оглавление
- •Введение
- •Задание 1
- •1 Постановка задачи
- •2 Решение нелинейных уравнений в средеdelphi
- •2.1 Отделение корней и предварительный анализ.
- •2.2. Уточнение корней
- •2.2.1 Уточнение корней методом касательных
- •2.2.2 Уточнение корней методом деления отрезка пополам
- •2.2.3 Уточнение корней методом хорд
- •2.2.4 Разработка программного продукта в среде Delphi
- •Результаты тестирования программного продукта
- •3 Вывод. Сравнение полученых результатов различными способами
- •Задание 2
- •1 Постановка задачи
- •2 Аппроксимация табулированных функций Метод наименьших квадратов
- •2.1 Решение задачи в средеDelphi
- •2.2 Решение задачи в среде mathcad
- •2.2.1 Находжение полинома 2,3,4 степеней и среднеквадратичные отклонения
- •3 Вывод. Результаты
- •Заключение
- •Список литературы
- •И с х о д н ы е д а н н ы е
2 Аппроксимация табулированных функций Метод наименьших квадратов
Очень часто, особенно при анализе эмпирических данных возникает необходимость найти в явном виде функциональную зависимость между величинами x и y , которые получены в результате измерений.
Эта таблица обычно
получается как итог каких-либо
экспериментов, в которых
![]() (независимая величина) задается
экспериментатором, а
(независимая величина) задается
экспериментатором, а![]() получается в результате опыта. Между
величинами x и y существует функциональная
зависимость, но ее аналитический вид
обычно неизвестен, поэтому возникает
практически важная задача – найти
эмпирическую формулу (2.1):
получается в результате опыта. Между
величинами x и y существует функциональная
зависимость, но ее аналитический вид
обычно неизвестен, поэтому возникает
практически важная задача – найти
эмпирическую формулу (2.1):
![]() (2.1)
(2.1)
где
![]() - параметры, значения которых при
- параметры, значения которых при![]() возможно мало отличались бы от опытных
значений
возможно мало отличались бы от опытных
значений![]() .
.
Если в эмпирическую
формулу (2.1) подставить исходные
![]() ,
то получим теоретические значения
,
то получим теоретические значения![]() ,
где
,
где![]() .
.
Разности
![]() называются отклонениями и представляют
собой расстояния по вертикали от точек
называются отклонениями и представляют
собой расстояния по вертикали от точек![]() до графика эмпирической функции. Согласно
методу наименьших квадратов наилучшими
коэффициентами
до графика эмпирической функции. Согласно
методу наименьших квадратов наилучшими
коэффициентами![]() считаются те, для которых сумма квадратов
отклонений найденной эмпирической
функции от заданных значений функции:
считаются те, для которых сумма квадратов
отклонений найденной эмпирической
функции от заданных значений функции:
![]() (2.2)
(2.2)
будет минимальной.
Поясним геометрический смысл метода наименьших квадралтов.
Каждая пара чисел
![]() из исходной таблицы определяет точку
из исходной таблицы определяет точку![]() на плоскости
на плоскости![]() .
Используя формулу (2.1) при различных
значениях коэффициентов
.
Используя формулу (2.1) при различных
значениях коэффициентов
![]() можно построить ряд кривых, которые
являются графиками функции (2.1). Задача
состоит в определении коэффициентов
можно построить ряд кривых, которые
являются графиками функции (2.1). Задача
состоит в определении коэффициентов![]() таким образом, чтобы сумма квадратов
расстояний по вертикали от точек
таким образом, чтобы сумма квадратов
расстояний по вертикали от точек![]() до графика функции (2.1) была наименьшей.
до графика функции (2.1) была наименьшей.
Построение эмпирической формулы состоит из двух этапов: выяснение общего вида этой формулы и определение ее наилучших параметров.
Если неизвестен характер зависимости между данными величинами x и y , то вид эмпирической зависимости является произвольным. Предпочтение отдается простым формулам, обладающим хорошей точностью. Большое значение имеет изображение полученных данных в декартовых или в специальных системах координат (полулогарифмической, логарифмической и т.д.). По положению точек можно примерно угадать общий вид зависимости путем установления сходства между построенным графиком и образцами известных кривых.
Для того, чтобы
найти набор коэффициентов
![]() ,
которые доставляют минимум функцииS
, определяемой формулой (2.2), используем
необходимое условие экстремума функции
нескольких переменных – равенство нулю
частных производных. В результате
получим нормальную систему для определения
коэффициентов
,
которые доставляют минимум функцииS
, определяемой формулой (2.2), используем
необходимое условие экстремума функции
нескольких переменных – равенство нулю
частных производных. В результате
получим нормальную систему для определения
коэффициентов
![]() :
:
![]() (2.3)
(2.3)
Таким образом,
нахождение коэффициентов
![]() сводится к решению системы (2.3).
сводится к решению системы (2.3).
Эта система
упрощается, если эмпирическая формула
(2.1) линейна относительно параметров
![]() ,
тогда система (2.3) – будет линейной.
,
тогда система (2.3) – будет линейной.
Конкретный вид
системы (2.3) зависит от того, из какого
класса эмпирических формул мы ищем
зависимость (2.1). В случае линейной
зависимости
![]() система (2.3) примет вид:
система (2.3) примет вид:
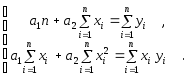 (2.4)
(2.4)
В случае квадратичной
зависимости
![]() система (2.3) примет вид:
система (2.3) примет вид:
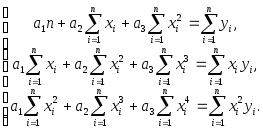 (2.5)
(2.5)
Эта линейная система может быть решена любым известным методом (методом Гаусса, простых итераций, формулами Крамера).
