Задание 1
1 Постановка задачи
Основной задачей первого задания курсовой работы является разработка программы в среде Delphi основанной на методе деления отрезка пополам, методе касательных и методе хорд для нахождения корней заданного уравнения.
Сформулируем задание на курсовую работу:
1. Графически определить корни уравнения в соответствии со своим вариантом. Параметр а задать самостоятельно путем подбора так, чтобы уравнение имело не менее трех корней. Определить, при каких значениях параметра а уравнение имеет один, два и три корня. Если уравнение не имеет указанного количества корней объяснить почему.
2. Разработать алгоритмы уточнения корней уравнения методом деления отрезка пополам, методом хорд и методом касательных. Построить блок-схемы алгоритмов.
3. На языке
программирования Pascal
(или Delphi)
создать программу для уточнения корней
уравнения указанными методами, реализующую
разработанные алгоритмы. С помощью
программы уточнить корни уравнения с
точностью
.
4. Решить задачу средствами MathCad или Excel.
5. Построить график функции F(x,a) от х для параметра а, использовавшегося при отделении и уточнении корней.
2 Решение нелинейных уравнений в средеdelphi
Рассмотрим решение задачи нахождения корней уравнения
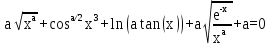
2.1 Отделение корней и предварительный анализ.
Анализ области допустимых значений (ОДЗ) для рассматриваемой функции:
Известно, что логарифма от нуля не существует, следовательно, X≠0 .
Известно, что при делении на нуль получается бесконечность. Принято, что деление на нуль не возможно, X≠0.
Подбор параметра
а
на основе анализа и построения графиков
функции
.
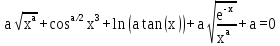Воспользуемся для построения графиков
программным пакетомMathcad.
При параметре a=0, график функции f(x) не имеет смысла, так как логарифма от нуля не существуют.
На рис. 2.1 показан график функции при a=1. Из графика видно, что при возрастании х, значение функции возрастает, но X≠0 (ОДЗ), отсутствует пересечение с осью 0х.
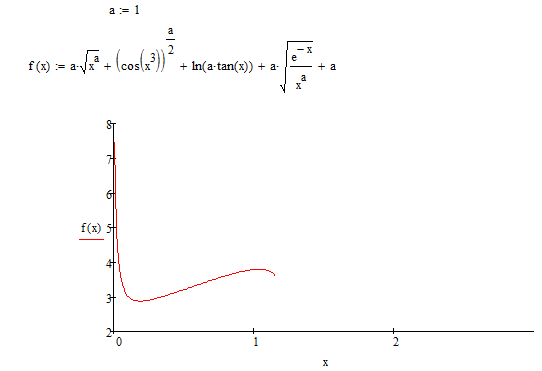
Рисунок 2.1 – График функции при a=1
На рис. 2.2 показан график функции при a=-1. Из графика видно, что при возрастании х отсутствует пересечение с осью 0х.
Рисунок 2.2 – График функции при a=-1
Используя Mathcad, подбором определим минимальное значение коэффициента а при котором рассмотренная функция имеет корни.
На рис.2.3 показан график заданной функции с наименьшим коэффициентом а=0,2 при котором функция имеет единственный корень.
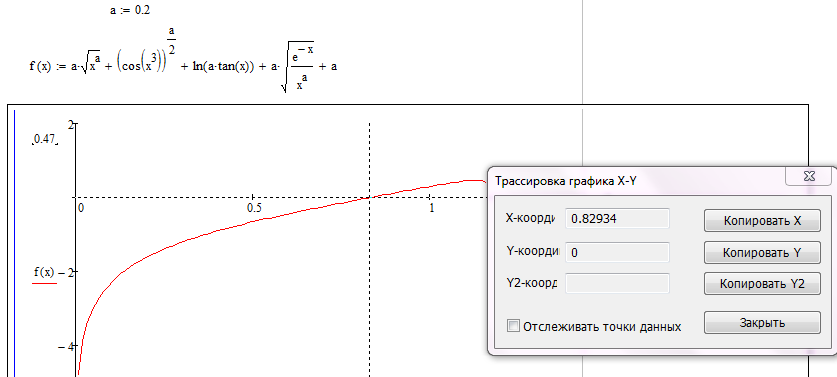
Рисунок 2.3 – График функции при а=0,2
Анализируя полученные графики, можно сделать вывод, что функция имеет корень, если а=0,2. Функция не имеет корней, если а равен любому другому значению. Функция может иметь только один корень.
Для последующих
расчетов а=0,2.
На графике рис.2.3 видно, что единственный
корень функции
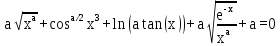принадлежит отрезку [0,5; 0,85].
Определим, для какого из концов отрезка выполняется условие сходимости метода
.(1)
На рис 2.4 представлены производные найденные средствами Mathcad.
Рисунок 2.4 – Расчет производных средствами Mathcad
На рис. 2.5 выполнена проверка условия (1) для обоих концов отрезка.
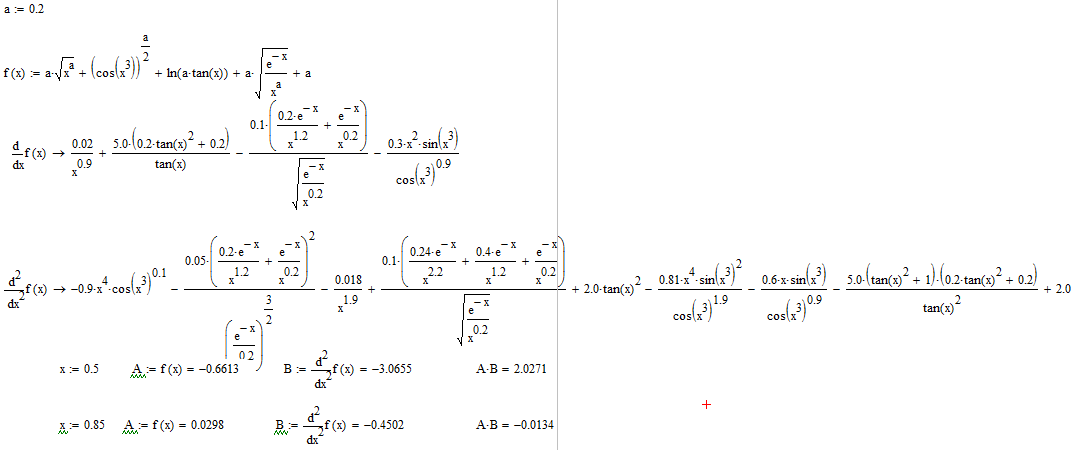
Рисунок 2.5 – Проверка условия сходимости средствами Mathcad
Таким образом, условие выбора начального приближения корня выполняется.
Погрешность данного метода на k-ом шаге оценивается по формуле:
, (2)
где M – минимальное значение модуля первой производной функции на отрезке [a; b].
На рис.2.6 показано определение минимального значение модуля первой производной функции на отрезке на отрезке [0,5; 0,85] средствами Mathcad.
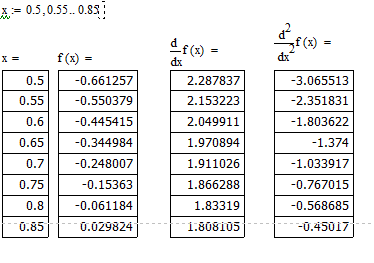
Рисунок 2.6
M=1,808105– минимальное значение модуля первой производной функции на отрезке [0.5; 0.85].