II Свойства сходящихся последовательностей и их пределов

1. Если последовательность сходится, то она ограничена (это свойство дока-зывается также, как аналогичное свойство б.м.)

2. Пусть . Тогда:

а) ;

б) ;

в) .

3.

4. Если , то все члены последовательности, начиная с некоторого номера, также положительны, и, более того, эти члены отграничены от нуля:.

Для доказательства достаточно в определении 3 положить . Очевидно, что подобное свойство справедливо и для.

5. Если и, тоограничена.

III Примеры вычисления пределов

1.

, ибо, аэталонная б.м.

2. это суммапервых членов геометрической прогрессии. Из элементарной математики известна формула для этой суммы

.

Если , тои. Значит. Если, тоимеет вид: 1, 0, 1, 0, … и предела не имеет. Остальные случаирассмотрим позже.

Задача (для самостоятельного решения). Пусть. Найти (если существуют) пределы следующих последовательностей: а); б); в); г).

§6. Бесконечно большие последовательности и их свойства

I Два определения

Определение 1 (язык «»). Последовательностьназывают бесконечно большой (б.б.) и пишут, если

.

Иными словами становится и остается больше любого наперед заданного сколь угодно большого числа.

Раскрывая неравенство с модулем, получим геометрическую иллюстрацию этого понятия.

Определение 2 (язык «окрестностей»). Последовательностьназывается б.б., если вне любой (сколь угодно большой)-окрестности нуля содержатся все члены последовательности, начиная с некоторого номера(зависящего от). Другими словами, внутри такой окрестности содержится лишь конечное число членов.

Замечание.Если члены б.б. последовательностиположительны (отрицательны), то можно писать.

О таких б.б. говорят, что они определенного знака.

II Две эталонных б.Б.

1. бесконечно большая. Примеры:

2. бесконечно большая. Примеры:.

Между б.б. и б.м. последовательностями существует естественная связь, устанавливаемая следующей теоремой.

Теорема.Для того, чтобы последовательностьбыла бесконечно большой, необходимо и достаточно, чтобы последовательностьбыла бесконечно малой.

Докажем, например, необходимость. Пусть б.б. Возьмем произвольноеи положим. Существует номер, начиная с которого. Тогда. Итак,. Это означает, что

.

III Свойства б.Б. Последовательностей

1. Пусть б.б. Тогда:

а) неограниченна;

б) ибесконечно большие;

в) бесконечно большая;

г) если , тобесконечно большая;

д) если , тобесконечно большая;

2. Произведение бесконечно больших последовательностей есть бесконечно большая.

Замечание 1.Сумма, разность и частное бесконечно больших может быть каким угодно.

Пример.Любой многочлен отесть б.б. Покажем это на конкретном примере:

.

Так как эталонная б.б., а, тоб.б.

Замечание 2.Запишем ряд б.б., отношения которых является б.м.:

Запись означает, что. Докажем, например, что. Обозначими. Тогда для

, т.к.. Следовательно, и.

Доказательство того, что

и

проведем позже, используя т.н. правило Бернулли-Лопиталя.

Лекция 4

§7. Теоремы о пределах последовательностей

Теорема 1..

Теорема 2( арифметические операции с пределами). Пусть последователь- ностиисходящиеся. Тогда сходящимися будут и такие последовательности:если только. При этом:

1)

2)

(здесь символ любой арифметической операции).

Ограничимся доказательством сходимости частного. Пусть , гдеи. Преобразуем частное следующим образом:

В полученном выражении, как линейная комбинация бесконечно малых, аограничена, т.к.. Следовательно,

. Это и доказывает:.

Теорема 3 (предельный переход в неравенствах). Пусть последовательностиисходящиеся. Тогда, если(или), то и. В частности:

а) если , то;

б) если , то.

Теорема 4 (достаточное условие сходимости). Еслии для всехсправедливо неравенство, то.

Для доказательства воспользуемся определением предела на языке окрестностей. Рассмотрим произвольную -окрестность числа. Обозначим ее. Так как, а так как. Тогда в силу неравенстваимеем:. Итак, для произвольной-окрестности мы нашли номер, начиная с которого членыпринадлежат этой окрестности. Это и означает, что.

Пример.Рассмотрим последовательность с общим членом.

Чтобы оценить сверху, заменим каждое слагаемое наибольшим (это первое слагаемое), а чтобы оценитьснизу, заменим слагаемые наименьшим (это последнее). Получим

или.

Подкоренные выражения обеих корней имеют вид , следовательно, сходятся к 1. Значит,.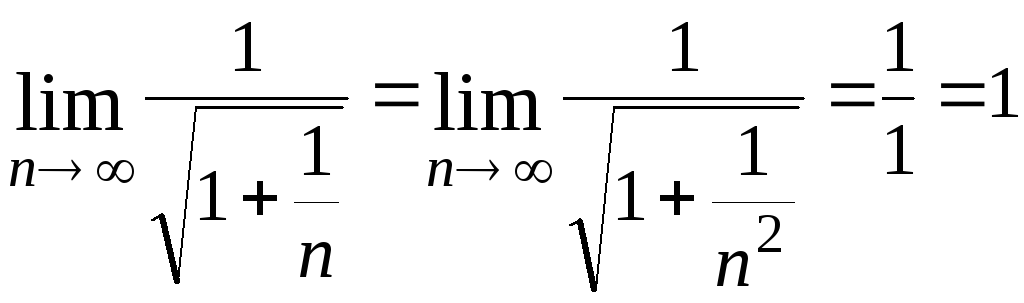

Отсюда вытекает, что .

Замечание 1.При решении примера было использовано одно свойство элементарных функций, вытекающее из их непрерывности: если членыи еёпринадлежат области определения элементарной функции, то знак предела можно вносить под знак функции

.

Замечание 2.Обратим внимание на следующее. Общий членпредставляет собой суммуслагаемых, каждое из которых является бесконечно малой. Однако, здесь нельзя сказать, что сумма б.м. есть б.м., ибо число слагаемых неограниченно возрастает.