II Элементарные функции
Определение.Элементарной называют функцию, котораяможет бытьзаданаявно однойформулой, содержащейконечное числоарифметических операций и суперпозиций, примененных к основным элементарным функциям.
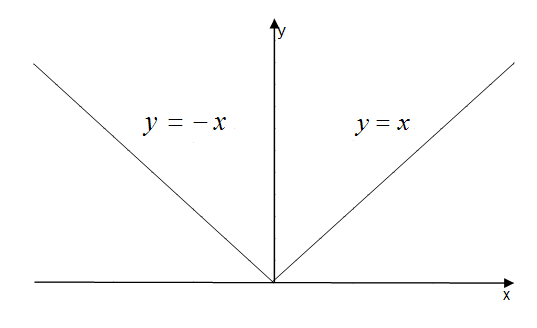
Следует отметить, что некоторые функции, заданные несколькими формулами (т.е., вообще говоря, неэлементарные) иногда удается записать одной формулой. Примером служит функция y = |x|. По определению
В то же время имеем:
.
Таким образом, функцияy
= |x|элементарная. Ее
график:
III Примеры неэлементарных функций
1)
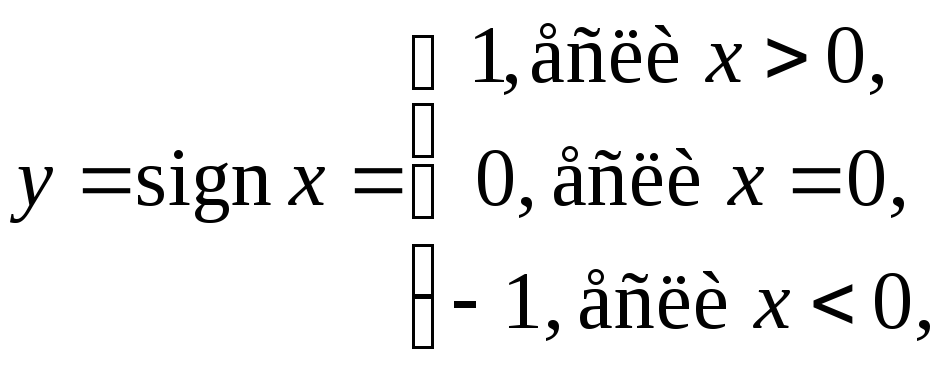
(читается «уравно сигнумх»).
2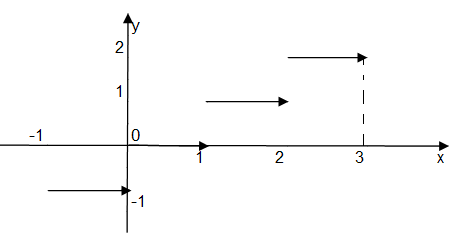
)y
= [x],где[x]целая
часть числаx
(читается «yравно антьеx»).
Эта функция неэлементарная, ибо задается не формулой, а словесно:
[x]наибольшее целое, не превосходящееx.
Отметим одно свойство:
.
y = {x}, где{x}дробная часть числаx, т.е.{x} = x [x].
Лекция 2
§3. Последовательности: основные понятия, примеры
I Определение
Пусть каждому натуральному числу nпо некоторому правилу поставлено в соответствие определенное числоxn: 1 x1, 2 x2, …, n xn, …Бесконечная совокупность этил чиселx1, x2, …, xn, … называется числовой последовательностью, сами числа называются членами последовательности,xn общий член последовательности. Краткая запись:{xn} «последовательность с общим членом xn».
Другими словами, последовательность – это функция натурального аргумента f(n).
Последовательность можно задавать:
1) аналитически,
например,
;
2) словесно, например, 2, 3, 5, 7, 11…последовательность простых чисел;
3)рекуррентным способом, например,
.
При этом способе задают первый или
несколько первых членов и формулу,
позволяющую определить любой член
последовательности по известным
предшествующим членам.
II Элементы поведения и операции
Как и для произвольной функции, для последовательности можно ввести понятия монотонности и ограниченности.
1) Последовательность {xn}
называется возрастающей (неубывающей),
если
для любогоn.
Если же для любогоnимеем неравенство
,
то последовательность называется
убывающей (невозрастающей).
2) Последовательность {xn}
называют ограниченной сверху, если
,
и ограниченной снизу, если
.
Последовательность называют ограниченной,
если она ограничена сверху и снизу.
Можно дать и другое определение
ограниченности:
.
Члены последовательности удобно
изображать точками на числовой оси.
Тогда ограниченность означает, что все
члены последовательности принадлежат
некоторому отрезку
,
а возрастание означает, что каждый
последующий член последовательности
расположен правее предшествующего.
Над последовательностями можно
осуществлять арифметические операции.
Например, сумма последовательностей
{xn}
и {yn}
это
последовательность{zn}такая, что
.
Аналогично определяют разность,
произведение и частное. Полезно уметь
представлять данную последовательность
как сумму или произведение двух других
последовательностей. Например,
есть
произведение
и
.
III Примеры
1)
стационарная
последовательность.
2)
ограниченная,
немонотонная.
3)
ограниченная снизу,
немонотонная.
4)
ограниченная,
возрастающая.
5)
это последовательность
с общим членом