- •Раздел дифференциальное исчисление Тема введение в математический анализ
- •§1. Функции одной переменной: основные понятия
- •I Определение
- •II Способы задания функции
- •III Область определения и область значения функции
- •IV График функции
- •V Действия над функциями
- •VI Элементы поведения функции
- •VII Обратная функция
- •§2. Элементарные функции
- •I Основные элементарные функции
- •II Элементарные функции
- •III Примеры неэлементарных функций
- •§3. Последовательности: основные понятия, примеры
- •I Определение
- •II Элементы поведения и операции
- •III Примеры
- •§4. Бесконечно малые последовательности и их свойства
- •I Два определения
- •II Две эталонные б.М.
- •III Основные свойства
- •§5 Предел последовательности
- •I Три определения
- •II Свойства сходящихся последовательностей и их пределов
- •III Примеры вычисления пределов
- •§6. Бесконечно большие последовательности и их свойства
- •I Два определения
- •II Две эталонных б.Б.
- •III Свойства б.Б. Последовательностей
- •§7. Теоремы о пределах последовательностей
- •§8. Монотонные последовательности. Число
- •I о пределе монотонной последовательности
- •II Число е
- •§9. Предел функции
- •I Общее определение
- •II Частные случаи. Важные понятия
- •III Односторонние пределы
- •IV Теоремы о пределах функций
- •§ 10. Замечательные пределы
- •I Первый замечательный предел
- •II Второй замечательный предел
- •§ 11. Эквивалентные б.М. И б.Б. Функции
- •I Сравнение б.М. И б.Б. Функций
- •II Эквивалентные функции: два определения
- •III Таблица эквивалентностей
- •IV Использование эквивалентностей для вычисления пределов
- •V Асимптотические формулы
- •§12. Понятие непрерывности функции
- •§13. Классификация точек разрыва
- •I Определение
- •II Точка устранимого разрыва
- •III Точка разрыва 1го рода
- •IV Точка разрыва 2го рода
- •§14. Основные свойства непрерывных функций
VII Обратная функция
Функцию y=f(x)называютобратимойна промежутке|a,b|, если любое свое значение она принимает не более чем в одной точке этого промежутка; иными словами, если различным значениям аргумента соответствуют различные значения функции.
Пусть обратимая функция y=f(x)задана на промежутке|a,b|и пустьE(y)=|A,B|.
Каждомуy|A,B|поставим в соответствие то единственное
значениеx[a,b],
для которогоf(x)=y.
Тем самым на|A,B|будет определена функция![]() ,
которую называютобратнойпо
отношению к функцииy=f(x).
,
которую называютобратнойпо
отношению к функцииy=f(x).
Отметим, что если
![]() обратная дляy=f(x),
то и функцияy=f(x)является обратной для
обратная дляy=f(x),
то и функцияy=f(x)является обратной для![]() .
Поэтому, эти две функции часто называютвзаимнообратными. Такие функции
обладают очевидными свойствами:
.
Поэтому, эти две функции часто называютвзаимнообратными. Такие функции
обладают очевидными свойствами:
![]() .
.
Графики взаимно обратных функций
совпадают. Можно, однако, потребовать,
чтобы и аргумент обратной функции
обозначался буквой x,
т.е. вместо![]() рассматривать функцию
рассматривать функцию![]() .
Графики такой пары функцийy=f
(x)и
.
Графики такой пары функцийy=f
(x)и![]() симметричны относительно прямойy=x.
симметричны относительно прямойy=x.
Можно доказать, что всякая строго монотонная функция имеет обратную, причем с тем же направлением монотонности.
Алгоритм нахождения обратной функции для функции y=f(x)следующий:
1) убедиться, что y=f(x)обратима (например, монотонная);
2) решить уравнение y=f(x)относительноx;
3) в полученном равенстве поменять местами xиy.
Пример. Найдем обратную
функцию для функции![]() (т.н. синус гиперболический).
(т.н. синус гиперболический).
а) Проверим монотонность. Пусть x1>x2.
Тогда![]() .
.
Функция y=ex– возрастающая, поэтому разность в
первой скобке положительна, аy=ex– убывающая, поэтому вторая разность
– отрицательна. Значит![]() ,
т.е
,
т.е![]() ,
т.е.y=
shx– возрастающая функция, следовательно,
обратимая.
,
т.е.y=
shx– возрастающая функция, следовательно,
обратимая.
б) Решим уравнение y=shx относительноx:
![]()
![]() – не подходит, ибо
– не подходит, ибо![]()
Итак,
![]() ,
т.е.
,
т.е.![]() .
.
в) Поменяв местами xиy, получим искомую обратную функцию:
![]() .
.
§2. Элементарные функции
I Основные элементарные функции
К основным элементарным функциям относят
константы, степенные, показательные,
логарифмические, тригонометрические
и обратные тригонометрические.
основным элементарным функциям относят
константы, степенные, показательные,
логарифмические, тригонометрические
и обратные тригонометрические.
1) Константыy = Const.
D(y) = R, E(y)={c}.
![]() не существует, четная.
не существует, четная.
График – прямая, параллельная оси абсцисс.
2 )Степенные
)Степенные
![]() .
.
D(y) иE(y) зависят от, но (0, +) D(y).
Четность-нечетность зависит от .
Обратная для
![]() есть
есть![]() .
.
Для <0 оси координат – асимптоты.
Показательные
 (0<a1).
(0<a1).
D(y) = R, E(y) = (0, +).
Функция общего вида.
Ось абсцисс – асимптота.
Обратная для функции
![]() есть логарифмическая функция
есть логарифмическая функция![]() .
.
Л
 огарифмическая
огарифмическая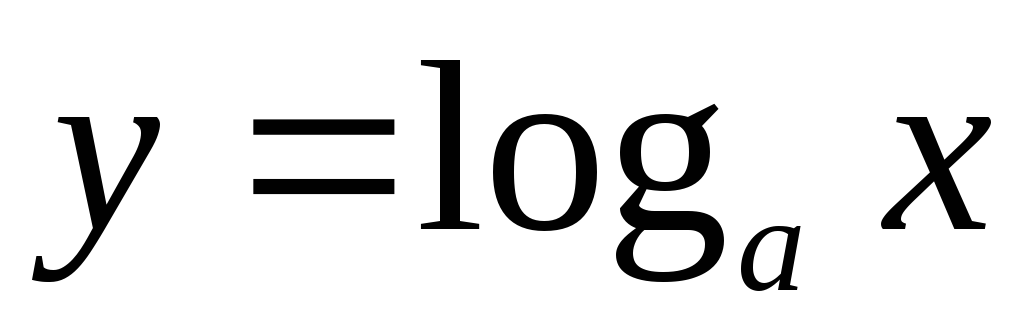 (0<a1).
(0<a1).
D(y) = (0, +), E(y) = R.
Функция общего вида.
Ось ординат – асимптота.
Обратная для логарифмической – показательная функция.
В математическом анализе в основном используют натуральные логарифмы lnx, т.е. логарифмы с основанием a=e=2,7…
5 ) Тригонометрические
) Тригонометрические
а)
![]() .
.
D(y) = R, E(y) = [1, 1].
Нечетная.
Периодическая,
![]() .
.

б)
![]() .
.
D(y) = R, E(y) = [1, 1].
Четная.
Периодическая,
![]() .
.
в )
)![]() .
.
D(y)
= R
\ {![]() ,
kz},
,
kz},
E(y) = R.
Нечетная.
Периодическая,
![]() .
.
Прямые
![]() асимптоты.
асимптоты.

г)
![]() .
.
D(y) = R \{k, kz}, E(y) = R
Нечетная.
Периодическая,
![]() .
.
Прямые x = kасимптоты.
6) Обратные тригонометрические
При определении этих функций выбираются
следующие участки монотонности: для
синуса ![]() ,
для косинуса[0,
],
для тангенса
,
для косинуса[0,
],
для тангенса![]() ,
для котангенса(0,
).
,
для котангенса(0,
).
Определение, например, арксинуса:
a rcsina
– это угол
rcsina
– это угол![]() такой, что
sin=a.
Остальные
функции
определяются аналогично.
такой, что
sin=a.
Остальные
функции
определяются аналогично.
а)
![]() .
.
D(y)
= [1,
1], E(y)
= ![]() .
.
Нечетная.
б )
)![]() .
.
D(y) = [1, 1], E(y) = [0, ].
arccos(x) = arccosx.
arcsinx
+ arccosx
=
![]() .
.

в)
![]() .
.
D(y)
= R,
E(y)
= ![]() .
.
Нечетная.
Прямые
![]() асимптоты.
асимптоты.
г )
)![]() .
.
D(y) = R, E(y) = (0, ).
arcctg(x) = arcctgx.
Прямые y = 0иy = асимптоты.
Замечание. Иногда к основным элементарным функциям относят еще и т.н. гиперболические функции и обратные к ним. Все эти функции достаточно просто выражаются через показательную и логарифмическую функции.
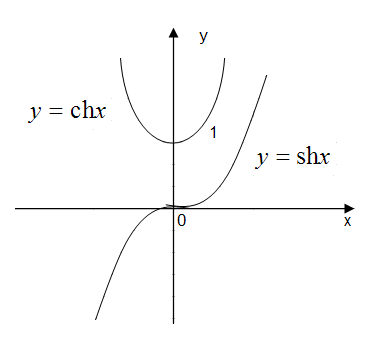
а) синус гиперболический
![]() :D(y)
= R,
E(y)
= R,
нечетная; обратная функция имеет видy
= Arshx
=
:D(y)
= R,
E(y)
= R,
нечетная; обратная функция имеет видy
= Arshx
=![]() .
.
б) косинус гиперболический
![]() :D(y)
= R,E(y)
= [1, +),
четная; обратная функция имеет видy
= Archx
=
:D(y)
= R,E(y)
= [1, +),
четная; обратная функция имеет видy
= Archx
=![]() ,
,![]() (у функцииchxберется ветвь
(у функцииchxберется ветвь![]() ).
).
в) тангенс и котангенс гиперболические определяются так же как и в тригонометрии:
![]() ,
,![]() .
.
Обратная функция для y
= thx– этоy
= Arthx
=
![]() .
Графики гиперболических функций:
.
Графики гиперболических функций: