§13. Классификация точек разрыва

I Определение

Точка x₀ называется точкой разрыва функцииf(x),если эта функция не является непрерывной в точкеx₀.

Определение непрерывности, т.е. равенство , подра-зумевает следующие три условия:

1) x₀  D(y);

2) существует и конечен;

3) .

При нарушении хотя бы одного из этих условий точка x₀и будет точкой разрыва. К точкам разрыва относят и те точки, не принадлежащие области определения функции, в окрестности (хотя бы односторонней) которых функция определена. Примером служит точкаx₀ =0 для функцийиy=lnx.

II Точка устранимого разрыва

Точкаx₀ называется точкой устранимого разрыва функцииy=f(x), если, существует и конечен, ноf(x₀)≠b или.

Например, функция

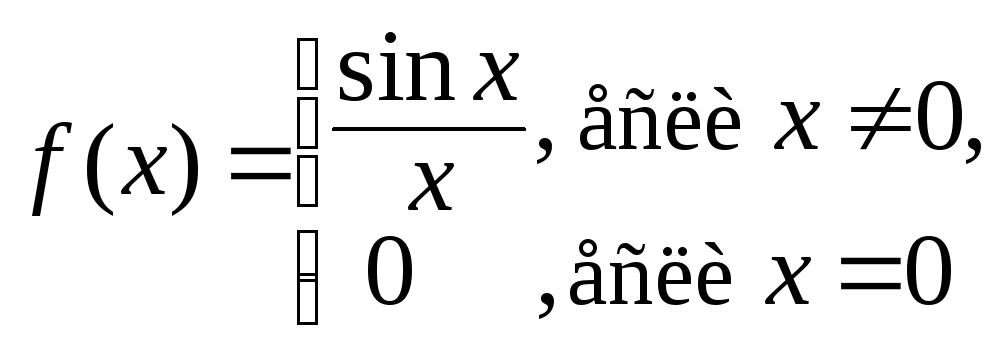
имеет в нуле устранимый разрыв, ибо , аf(0)=0≠1. Еще один пример дает функция, которая не определена в нуле, носуществует и конечен.

III Точка разрыва 1го рода

Точка x₀называется точкой разрыва 1^города функцииf(x), если в этой точке

функция имеет конечные, но не равные друг другу односторонние пределы:

f(x₀+0)≠ f(x₀ – 0).

Сама точка x₀при этом может, как принадлежать, так и не принадлежать областиD(y).

Разность f(x₀+0) – f(x₀ – 0) называется скачком функции в точкеx₀.

Примеры.

1) f(x)=signx: f(0+0)=1, f(0–0)= –1.

2) f(x)=[x]: для любой целой точкиf(k+0)=k,f(k–0)=k–1.

3) f(x)=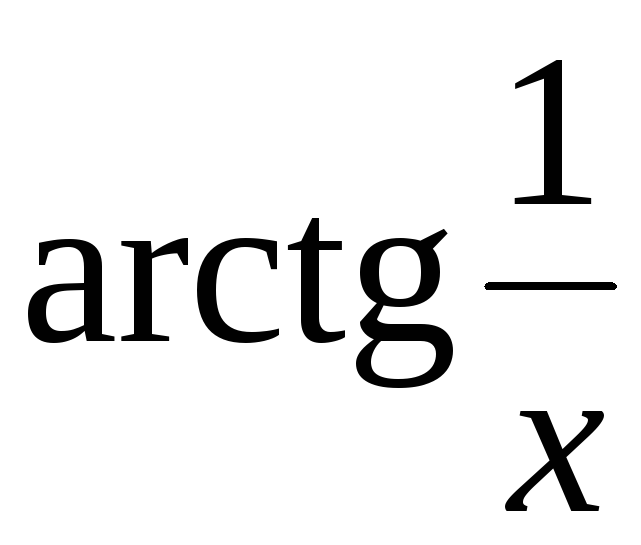:f.

4) f(x)=(самостоятельно).

IV Точка разрыва 2го рода

Точка x₀называется точкой разрыва 2^города функцииy=f(x), если в этой точке, хотя бы один из односторонних пределов функции равенили не существует.

Примеры.5) Дляf(x)=в примере 4 §9 получено:f(0+0)=+.

6) f(x)=в нуле не имеет предела, ибо для последовательности значений аргумента, сходящейся к нулю, соответствующая последовательность значений функциине имеет предела.

7) См. пример 2 §9.

Замечание 1.При исследовании функции на непрерывность необходимо различать элементарные и неэлементарные функции. Например,– элементарная, следовательно, непрерывная всюду наD(y), а точки, не принадлежащиеD(y), – это точки разрыва. Их тип устанавливается путем вычисления односторонних пределов. Функция же

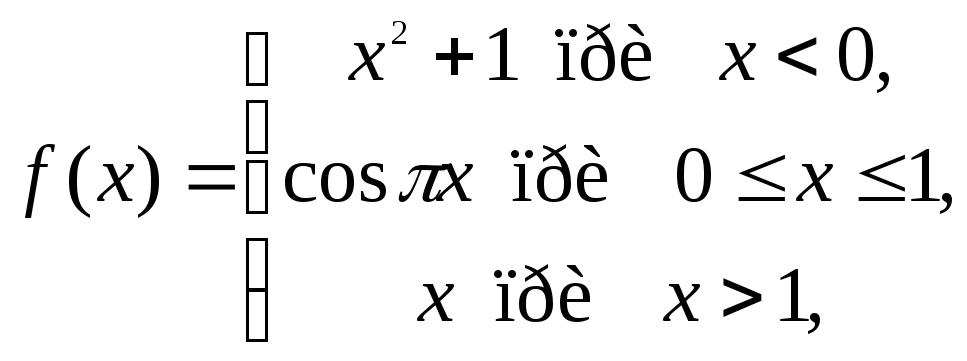
не является, вообще говоря, элементарной, поэтому может иметь разрыв в любой точке. Но каждое из трех выражений, определяющих функцию, есть элементарное, а значит, непрерывно. Эта функция может иметь разрывы только в точках, в которых переходит с одного выражения на другое. Итак, точки возможного разрыва

Замечание 2.Монотонная ограниченная функция может иметь разрывы только 1^города (следствие теоремы 12 §9).

§14. Основные свойства непрерывных функций

1. Устойчивость знака.Если функцияf(x)непрерывна в точкеx₀ иf(x₀)≠0, то в некоторой окрестности точкиx₀функцияf(x) сохраняет знак.

2. Локальная ограниченность.Если функцияf(x)непрерывна в точкеx₀, то она ограничена в некоторой окрестности точкиx₀.

3. Ограниченность на промежутке(1^ятеорема Вейерштрасса). Если функцияf(x)непрерывна на замкнутом промежутке, то она ограничена на этом промежутке.

4. Достижение наибольшего и наименьшего значений(2^ятеорема Вейерштрасса). Если функцияf(x)непрерывна на замкнутом промежутке, то она достигает своих наибольшего и наименьшего значений, т.е.,:

.

5. Прохождение через ноль(1^ятеорема Больцано-Коши). Пусть функцияf(x)непрерывна на промежуткеи на его концах имеет значения разных знаков. Тогда. Если жеf(x)еще и строго монотонная, то такая точка единственная.

Пример использования этого свойства: доказать, что уравнение имеет корень на интервале (0,1). Рассмотрим функцию. Она непрерывна всюду (как элементарная) и, а– значения разных знаков. Значит,. Это числоcи есть корень уравнения.

На этом свойстве основан метод интервалов решения неравенств: непрерывная функция между своими нулями сохраняет знак.

6. Прохождение через промежуточные значения(2^ятеорема Больцано-Коши). Пусть функцияf(x)непрерывна на промежутке, причем. Тогда

.

Другими словами, непрерывная функция, переходя от одного значения к другому, принимает и все промежуточные значения.

7. Существование обратной функции.Непрерывная строго монотонная функция имеет обратную также непрерывную строго монотонную с тем же направлением монотонности.

43