
- •Раздел дифференциальное исчисление Тема введение в математический анализ
- •§1. Функции одной переменной: основные понятия
- •I Определение
- •II Способы задания функции
- •III Область определения и область значения функции
- •IV График функции
- •V Действия над функциями
- •VI Элементы поведения функции
- •VII Обратная функция
- •§2. Элементарные функции
- •I Основные элементарные функции
- •II Элементарные функции
- •III Примеры неэлементарных функций
- •§3. Последовательности: основные понятия, примеры
- •I Определение
- •II Элементы поведения и операции
- •III Примеры
- •§4. Бесконечно малые последовательности и их свойства
- •I Два определения
- •II Две эталонные б.М.
- •III Основные свойства
- •§5 Предел последовательности
- •I Три определения
- •II Свойства сходящихся последовательностей и их пределов
- •III Примеры вычисления пределов
- •§6. Бесконечно большие последовательности и их свойства
- •I Два определения
- •II Две эталонных б.Б.
- •III Свойства б.Б. Последовательностей
- •§7. Теоремы о пределах последовательностей
- •§8. Монотонные последовательности. Число
- •I о пределе монотонной последовательности
- •II Число е
- •§9. Предел функции
- •I Общее определение
- •II Частные случаи. Важные понятия
- •III Односторонние пределы
- •IV Теоремы о пределах функций
- •§ 10. Замечательные пределы
- •I Первый замечательный предел
- •II Второй замечательный предел
- •§ 11. Эквивалентные б.М. И б.Б. Функции
- •I Сравнение б.М. И б.Б. Функций
- •II Эквивалентные функции: два определения
- •III Таблица эквивалентностей
- •IV Использование эквивалентностей для вычисления пределов
- •V Асимптотические формулы
- •§12. Понятие непрерывности функции
- •§13. Классификация точек разрыва
- •I Определение
- •II Точка устранимого разрыва
- •III Точка разрыва 1го рода
- •IV Точка разрыва 2го рода
- •§14. Основные свойства непрерывных функций
III Таблица эквивалентностей
При
![]() :
:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
;
3)
![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
9)
;
9)![]() ;
;
10)
![]() ;
11)
;
11)![]() ;
12)
;
12)![]() ;
;
13)
![]() .
.
Кроме этих формул используются еще такие:
14) многочлен на
![]() эквивалентен старшему члену, а в нулемладшему;
эквивалентен старшему члену, а в нулемладшему;
15)
![]() при
при![]() ,
если только
,
если только![]() и
и![]() ;
;
16)
![]() ,
,![]() при
при![]() (
(![]() ,
,![]() );
);
17)
![]() при
при![]() .
.
Часть этих формул была получена в §10. Выведем еще несколько других:
5)
![]() ;
;
10)
![]() ;
;
13)
![]() ;
;
15) Пусть
![]() ,
Тогда
,
Тогда![]() ,
т.е.
,
т.е.
![]() (в широком смысле).
(в широком смысле).
IV Использование эквивалентностей для вычисления пределов
Теорема.Пусть![]() ,
а
,
а![]() при
при![]() .
Если
.
Если![]() ,
то и
,
то и![]() .
.
Доказательство.
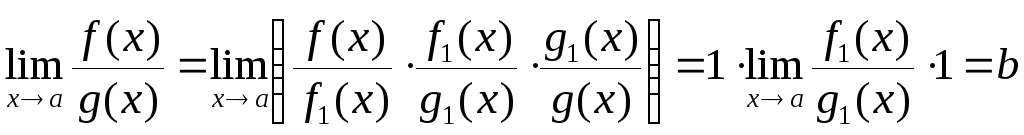 .
.
Практический вывод.При вычислении пределов частных и произведений функций каждую из них можно заменить эквивалентной.
Примеры.
4.

![]() .
.
Здесь были использованы эквивалентности для синуса, логарифма, арктангенса, степенной функции и выражения типа многочлена (алгебраической суммы степеней переменной с неотрицательными показателями, а не только натуральными, как в обычном многочлене).
5. Вычислим предел
![]() .
Используя основное логариф-мическое
тождество, свойство логарифма степени
и непрерывность функции
.
Используя основное логариф-мическое
тождество, свойство логарифма степени
и непрерывность функции![]() ,
получим:
,
получим:
 .
.
Выведем нужную здесь формулу эквивалентности
при
![]() :
:
![]() .
.
Итак,
 .
.
6. Приведем ряд примеров «подгонки» под табличную форму эквивалент-ности:
![]() при
при![]() ;
;
![]() при
при![]() ;
;
![]() при
при![]() .
.
Замечание-предостережение.Использовать эквивалентности (в указанной
форме![]() )
в суммах, разностях функций и под знаками
функций, вообще говоря, нельзя. Исключение
составляет степенная функция, т.е., если
)
в суммах, разностях функций и под знаками
функций, вообще говоря, нельзя. Исключение
составляет степенная функция, т.е., если![]() ,
то
,
то![]() ,
,![]() .
.
Однако, существует другая форма эквивалентностей, которую можно использовать везде. Эту форму рассмотрим в следующей части параграфа.
V Асимптотические формулы
В силу второго определения эквивалентности
соотношения
![]() равносильно
равносильно![]() или
или![]() .
Таким образом, таблицу эквивалентностей
можно записать в форме т.н. асимптотических
формул. Приведем лишь некоторые из них.
Все остальные студенты должны уметь
выводить самостоятельно.
.
Таким образом, таблицу эквивалентностей
можно записать в форме т.н. асимптотических
формул. Приведем лишь некоторые из них.
Все остальные студенты должны уметь
выводить самостоятельно.
Итак, при
![]() :
:
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Эти асимптотические формулы можно применять в суммах, разностях и под знаками функций. Однако, не всегда они дают ответ на поставленный вопрос.
Примеры.
7.
![]()

 .
.
Здесь использован тот факт, что по
определению символа
![]() имеем:
имеем:![]() .
.
8.
![]() =
– частное бесконечно малых может быть
любым. Такая ситуация означает, что
соответствующая асимптотическая формула
недостаточно точная. В теме «Формулы
Тейлора и Маклорена» будут даны уточнения:
=
– частное бесконечно малых может быть
любым. Такая ситуация означает, что
соответствующая асимптотическая формула
недостаточно точная. В теме «Формулы
Тейлора и Маклорена» будут даны уточнения:
![]() ,
,![]() .
.
Задача.Вычислить пределы:
а)
![]() ;
б)
;
б)![]() .
.
Лекция 7
§12. Понятие непрерывности функции
Рассмотрим функцию y=f(x), определенную в точкеx0и в некоторой ее окрестности.
Определение 1.Функцияf(x)называется непрерывной в точкеx0, если
![]() . (1)
. (1)
Так как
![]() ,
то соотношение (1) можно записать в
следующем виде:
,
то соотношение (1) можно записать в
следующем виде:
![]() ,
,
т.е. для непрерывной функции можно знак предела вносить под знак функции.
Дадим еще одно определение непрерывности равносильное определению 1. Для этого в равенстве (1) перенесем f(x0) в левую часть и внесем под знак преде-
ла. Так как условия x![]() x0и (x
– x0)
x0и (x
– x0)![]() 0
равносильны, то получаем:
0
равносильны, то получаем:
![]() (2)
(2)
Разность x – x0 называется приращением аргументаxв точкеx0 и обозначаетсяΔx, а разностьf(x)– f(x0) – приращением функции и обозначаетсяΔy. В этих обозначениях равенство (2) принимает вид:
![]() . (3)
. (3)
Это соотношение и есть еще одно определение непрерывности, которое можно сформулировать так:
Определение 2.Функцияf(x)называется непрерывной в точкеx0,
если ее приращениеΔy=o(1)приΔx![]() 0.
0.
Пример.Докажем непрерывностьy=sinx в произвольной точкеx0 .
![]()
Полученное выражение есть произведение
ограниченной функции
![]() на бесконечно малую (в силу леммы 2 §10
на бесконечно малую (в силу леммы 2 §10
 приΔx
приΔx![]() 0
). По одному из свойств б.м. функций
получаемΔy=o(1)приΔx
0
). По одному из свойств б.м. функций
получаемΔy=o(1)приΔx![]() 0,
что и доказывает непрерывностьy=sinx
в произвольной точкеx0
.
0,
что и доказывает непрерывностьy=sinx
в произвольной точкеx0
.
Определение 3.Функцияf(x) называется непрерывной в точкеx0 слева (справа), если
![]()
![]() .
.
Например, функция y=[x]непрерывна справа в любой целой точке, т.к.[k+0]=[k]=k, в то же время слева она не является непрерывной[k–0]=k–1≠[k].
Из общих теорем о пределах функций легко получить такие результаты.
Теорема 1.Функцияf(x) непрерывна в точкеx0 тогда и только тогда, когда она непрерывна в этой точке, как справа, так и слева, т.е.
f(x0+0)= f(x0 – 0)= f(x0)
Теорема 2.Пусть функцииf(x)иg(x)непрерывны в точкеx0, а функцияF(u)непрерывна в точкеu0=f(x0).Тогда и функцииf(x)±g(x), f(x)·g(x), f(x):g(x) (при условииg(x0)≠0 ) иF(f(x)) непрерывны в точкеx0.
Если бы мы могли доказать непрерывность всех основных элементарных функций (как мы это сделали для синуса), то из теоремы 2 мы получили бы еще один важный результат.
Теорема 3.Всякая элементарная функция непрерывна в любой точке ее области определения (входящей в эту область с некоторой окрестностью).
Определение 4.Говорят, что
функцияf(x)
непрерывна на промежутке![]() ,
если она непрерывна в любой точке
промежутка (в граничных точках промежутка
подразумевается одностороння
непрерывность).
,
если она непрерывна в любой точке
промежутка (в граничных точках промежутка
подразумевается одностороння
непрерывность).
