5.2 Прямые методы

5.2.1 Правило Крамера

Можно использовать лишь для решения систем состоящих из нескольких (n=2, n=3) уравнений.

Согласно этого правила, каждое неизвестное представляется в виде отношения определителей. Запишем его для системы из двух уравнений

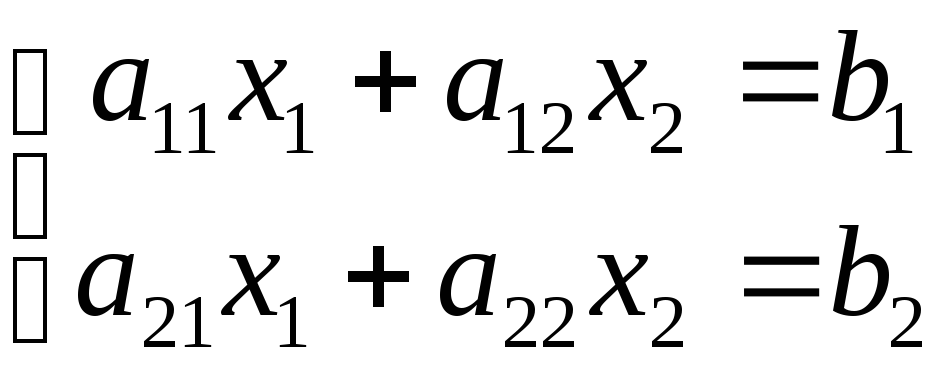
Можно попытаться использовать это правило для решения систем уравнений произвольного порядка. Однако при большом числе уравнений потребуется выполнить огромное число ((n+1)(n*n!-1)+n) арифметических операций для вычисления n+1 определителя (без использования экономичных методов).

5.2.2 Метод обратной матрицы

Система записывается в виде (5.3)

Умножая обе части этого уравнения на матрицу , обратную матрицеполучим

Если не использовать экономичных схем для вычисления обратной матрицы, этот способ также не пригоден для практического решения линейных систем при больших значениях n из-за большого объема вычислений

5.2.3 Метод Гаусса (метод исключения Гаусса)

Наиболее распространенный среди прямых методов для решения систем при n<10. Он основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается х₁ из всех последующих уравнений системы. Затем с помощью второго уравнения исключается х₂ из третьего и всех последующих уравнений системы и т.д. Этот процесс называется прямым ходом метода Гаусса и продолжается до тех пор, пока в левой части последнего n-го уравнения не останется лишь один член с неизвестным х_n, то есть матрица системы будет приведена к треугольному виду.

Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных. Решая последнее уравнение, находим единственное неизвестное х_n. Далее, используя это значение, из предыдущего уравнения, вычисляем х_n-1 и т. д. Последним найдем х₁ из первого уравнения.

Рассмотрим применение метода Гаусса для системы из 3-х уравнений с 3-мя неизвестными.

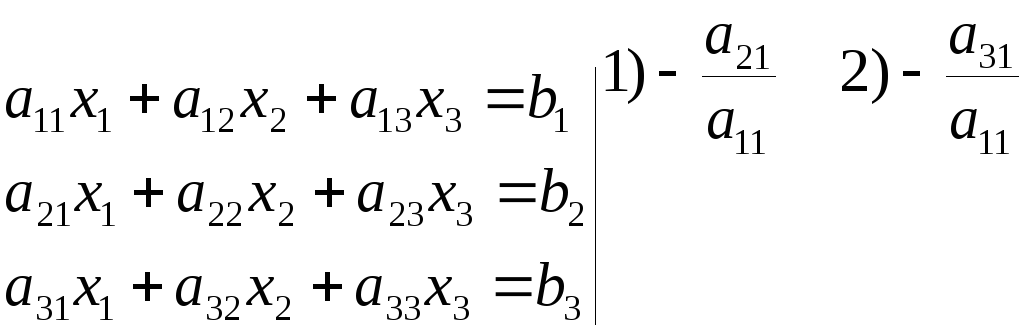
1)

2)

Матрица системы имеет треугольный вид. На этом заканчивается прямой ход метода Гаусса.

Заметим, что в процессе исключения неизвестных приходится выполнять операции деления на коэффициенты а₁₁, a’₂₂ и т. д., которые называются ведущими элементами. Поэтому они должны быть отличны от нуля. В противном случае необходимо соответственным образом переставить уравнения системы.

Обратный ход

Такой порядок метода Гаусса называется схемой единственного деления.

Одной из модификаций метода Гаусса является схема с выбором главного элемента. Она состоит в том, что требование неравенства нулю ведущих элементов, на которые происходит деление в процессе исключения, заменяется более жестким: из всех оставшихся в к-ом столбце элементов нужно выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте ведущего элемента.

Модификацией метода Гаусса является и схема Жордана, при которой матрица системы А приводится к диагональному виду, то есть все элементы, кроме элементов на главной диагонали, должны быть равны 0. Особых преимуществ нет. Облегчается обратный ход, усложняется прямой, так как увеличивается число операций.

Модификацией метода Гаусса есть и метод прогонки. Он используется для решения частного случая разреженных систем линейных уравнений – уравнений с трех диагональной матрицей коэффициентов. Такие системы получаются при численном решении краевых задач для дифференциальных уравнений.

Запишем систему уравнений в виде

b₁x₁+c₁x₂+… =d₁

a₂x+b₂x₂+c₂x₃+… =d₂

0+a₃x₂+b₃x₃+c₃x₄+… =d₃

…

a_n-1x_n-2+b_n-1x_n-1+c_n-1x_n=d_n-1

a_nx_n-1+b_nx_n=d_n

Метод прогонки состоит из двух этапов : прямой прогонки (аналог прямого хода метода Гаусса) и обратной прогонки (аналога обратного хода метода Гаусса). Прямая прогонка состоит в том, что каждое неизвестное x_i выражается через x_i+1 с помощью прогоночных коэффициентов

x_i=A_ix_i+1+B_i i=1,2,…,n-1

Из первого уравнения

x₁=A₁x₂+B₁

Из второго уравнения

a₂(A₁x₂+B₁)+b₂x₂+c₂x₃=d₂

a₂A₁x₂+ a₂B₁+b₂x₂+c₂x₃=d₂

x₂(a₂A₁+ b₂)+a₂B₁+c₂x₃=d₂

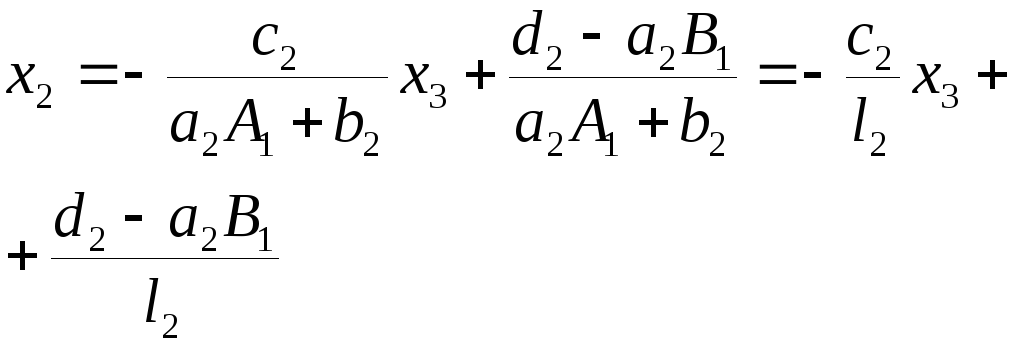
x₂=A₂x₃+B₂

l₂=a₂A₁+b₂

Аналогично можно вычислить прогоночные коэффициенты для любого i

,

l_i=a_iA_i-1+b_i i=2,…,n-1

Таким образом

x_n-1=A_n-1x_n+B_n-1

Далее выполняется обратная прогонка, для чего сначала вычисляется x_n из последнего уравнения

a_nx_n-1+b_nx_n=d_n

a_n(A_n-1x_n+B_n-1)+b_nx_n=d_n

a_nA_n-1x_n+ a_n B_n-1+b_nx_n=d_n

x_n(a_nA_n-1+b_n)+a_n B_n-1=d_n

Затем x_n-1, используя формулу

x_n-1=A_n-1x_n+B_n-1

и формулы для прогоночных коэффициентов.

При вычислении A_i и B_i надо учитывать возможность деления на 0. Чтобы этого не произошло желательно, чтобы в таких системах выполнялось условие преобладания диагональных элементов, то есть |b_i|≥|a_i|+|c_i| и хотя бы для одного i неравенство должно быть строгим.