ЧМ_стац / Численные методы лекции / 4. Приближенное интегрирование

4. Приближенное интегрирование функций

4.1 Общие сведения.

Пусть на отрезке задана функция . С помощью точек разобьем отрезок на элементарных отрезков , , причем .

На каждом из этих отрезков выбираем произвольную точку и найдем произведение значения функции в этой точке на длину элементарного отрезка

(4.1)

Составим сумму всех таких произведений

(4.2)

Сумма называется интегральной суммой.

Определенным интегралом от функции на отрезке называется предел интегральной суммы при неограниченном увеличении числа точек разбиения. При этом длина наибольшего из элементарных отрезков стремится к нулю.

(4.3)

Геометрический смысл проиллюстрируем на рисунке

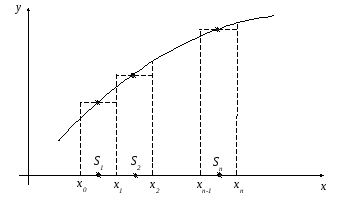
Выражения (4.1) описывают площади элементарных прямоугольников, интегральная сумма (4.2) – площадь ступенчатой фигуры, образуемой этими прямоугольниками.

При неограниченном увеличении числа точек деления и стремлении к нулю всех элементов верхняя граница фигуры (ломаная) переходит в линию . Площадь полученной фигуры, которую называют криволинейной трапецией, равна определенному интегралу.

Если подынтегральная функция задана в аналитическом виде , непрерывна на отрезке и известна ее первообразная , то определенный интеграл от этой функции в пределах от до может быть вычислен аналитически по формуле Ньютона-Лейбница:

.

Однако на практике этой формулой часто нельзя воспользоваться по двум основным причинам:

1. Вид функции не допускает непосредственного интегрирования, т.е. первообразная не может быть найдена с помощью элементарных средств или является слишком сложной.

2. Значения функции заданы таблично, т.е. на фиксированном конечном множестве точек .

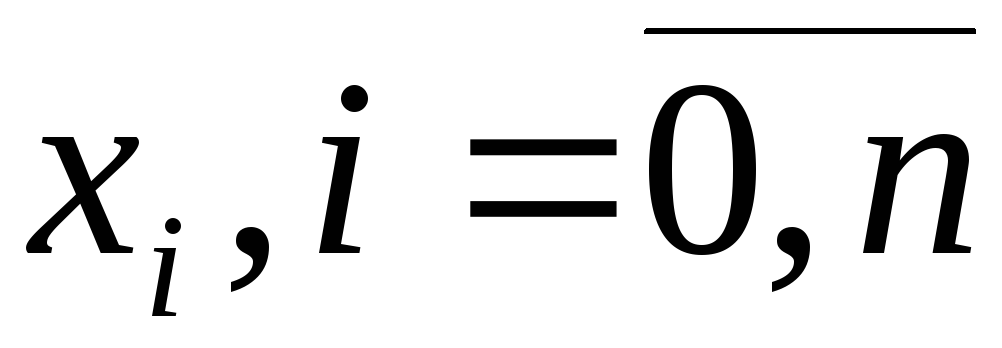Поэтому важное значение имеют приближенные и, в первую очередь, численные методы вычисления определенных интегралов.

Приближенные методы рассмотрим на примере представления подынтегральной функции в виде степенного ряда (ряда Тейлора), что позволит свести вычисление интеграла от сложной функции к интегрированию многочлена, представляющего собой первые несколько членов ряда.

Пример. Вычислить интеграл с погрешностью .

Воспользуемся разложением экспоненты в ряд: .

Используя данный ряд, и заменяя в нем на , записываем интеграл

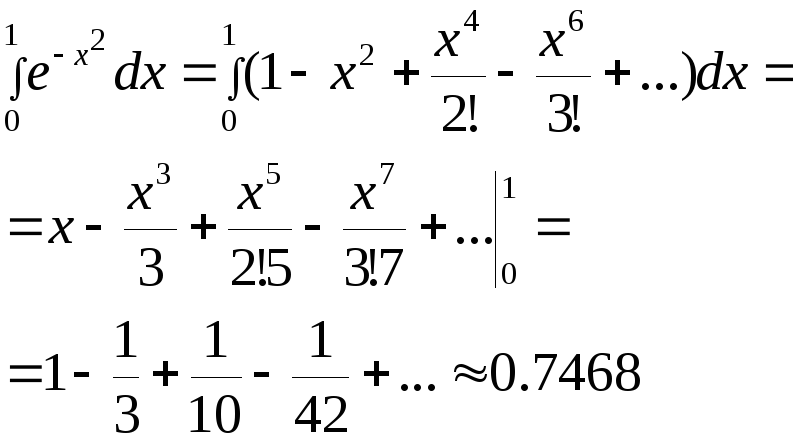
Методы численного интегрирования являются универсальными методами, которые пригодны для обоих случаев. Они основаны на аппроксимации подынтегральной функции интерполяционными многочленами.

Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции, т.е. заданной таблично.

Численное вычисление однократного интеграла называется механической квадратурой. Поэтому соответствующие формулы называются квадратурными.

4.2 Метод прямоугольников

Простейший метод численного интегрирования. Он использует локальное интерполирование многочленом нулевой степени вида

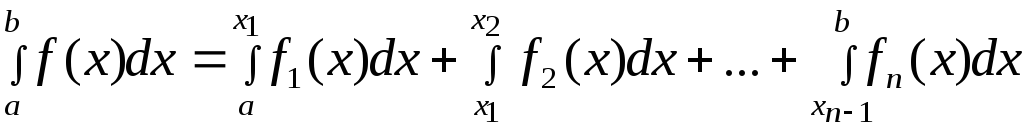
на каждом из отрезков .

В качестве могут быть выбраны значения функции на левых концах или на правых концах отрезка

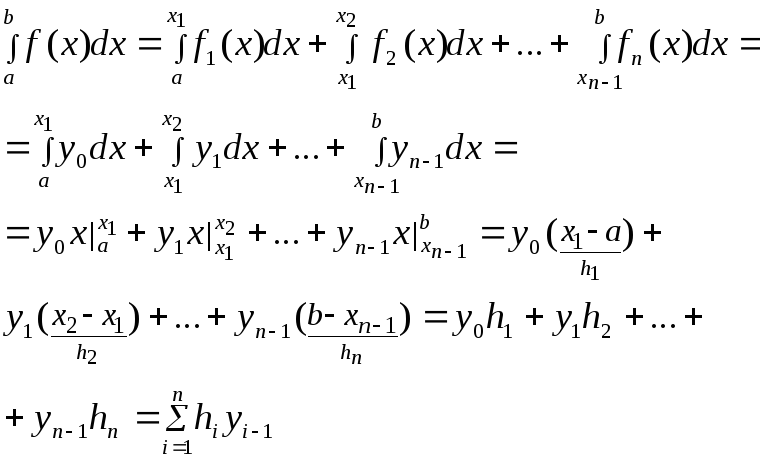(4.5)

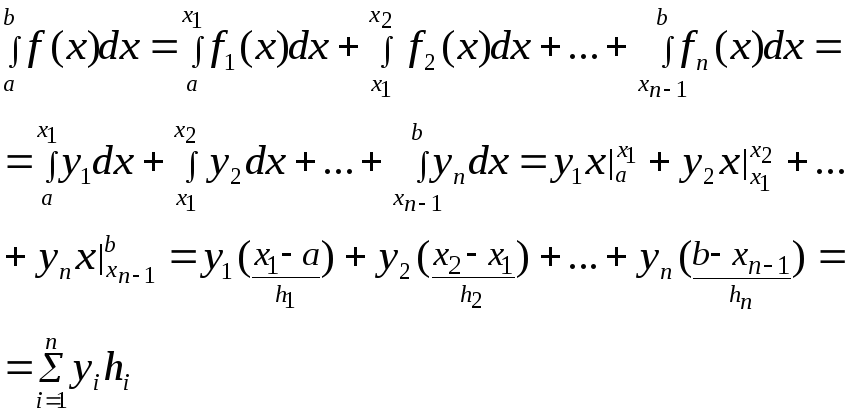(4.6)

Более точным является вид формулы прямоугольников, использующий значение функции в средних точках элементарных отрезков (в так называемых полуцелых узлах)

(4.7)

Формулы (4.5)-(4.7) соответственно называются формулами:

Левых прямоугольников

Правых прямоугольников

Средних прямоугольников.

Важным случаем рассмотренных формул (4.5)-(4.7) является их применение при численном интегрировании с постоянным шагом

(4.8)

(4.9)

(4.10)

4.3 Метод трапеций

Использует локальную линейную интерполяцию, то есть график функции f(x) представляется в виде ломаной, соединяющей точки с координатами (). В этом случае подынтегральная функция на элементарных отрезках представляется многочленом первой степени вида

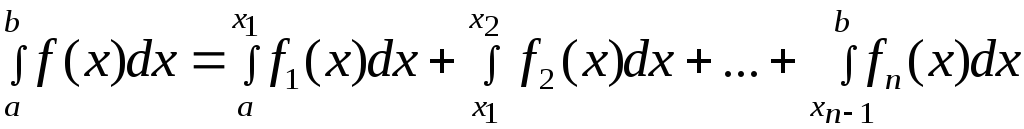
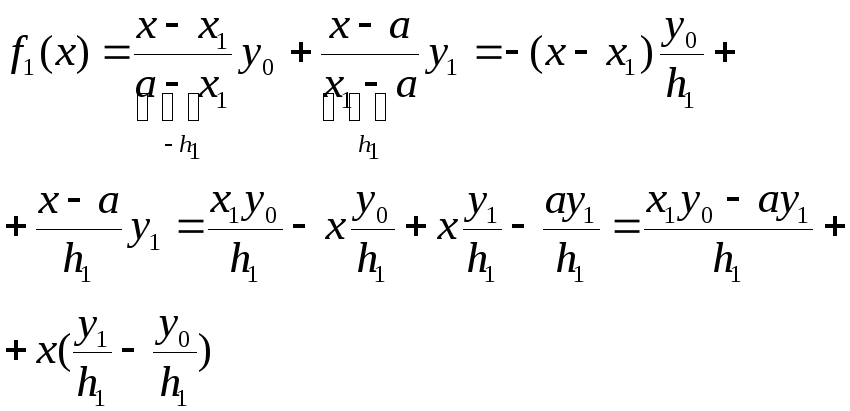
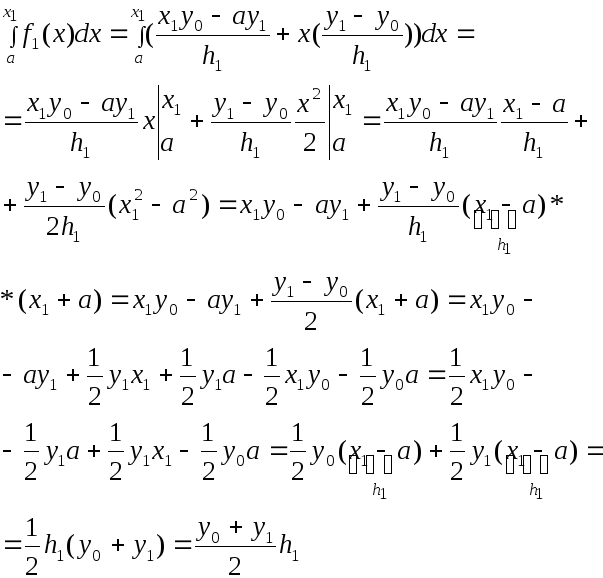
Аналогично

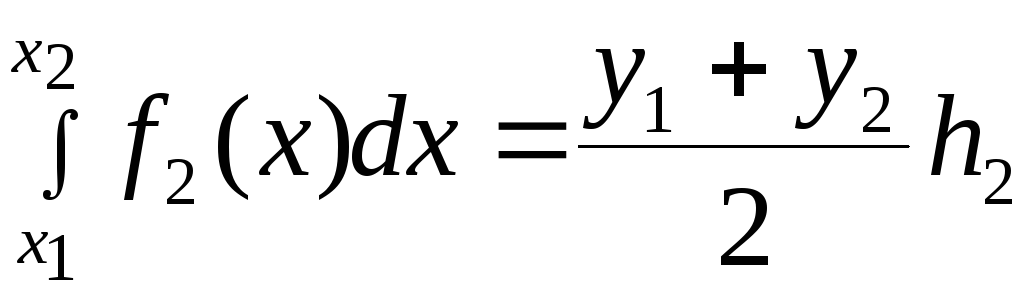
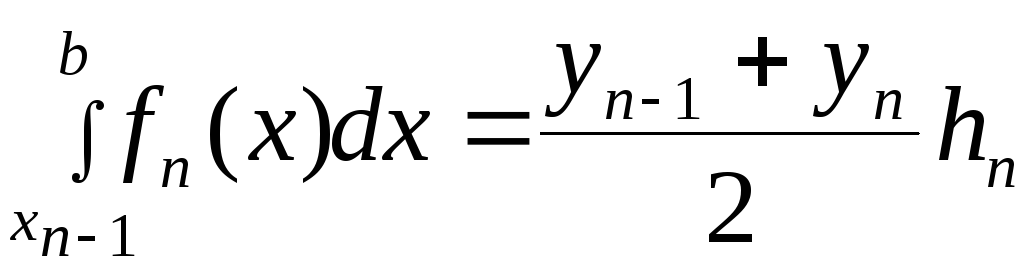
Таким образом

(4.11)

Для случая равноотстоящих узлов

(4.12)

4.4 Метод Симпсона (метод парабол)

Использует представление подынтегральной функции в виде многочлена 2-ой степени вида , что требует разбиения отрезка интегрирования [a,b] на четное число отрезков одинаковой длины h=const

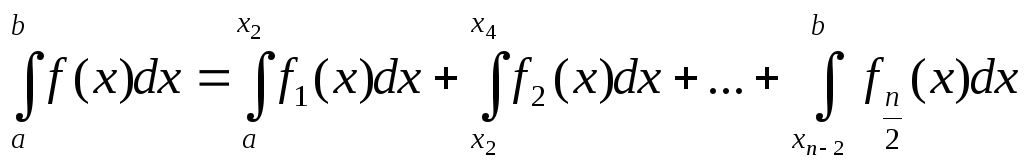
В качестве f_i(x), i=1,n/2 можно использовать многочлен Лагранжа, проходящий через три точки

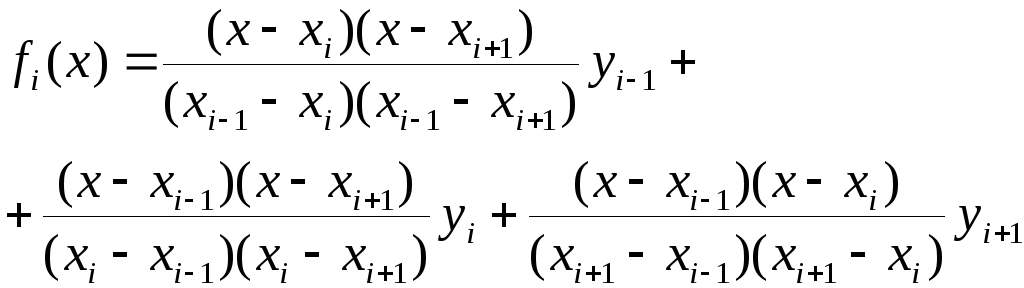
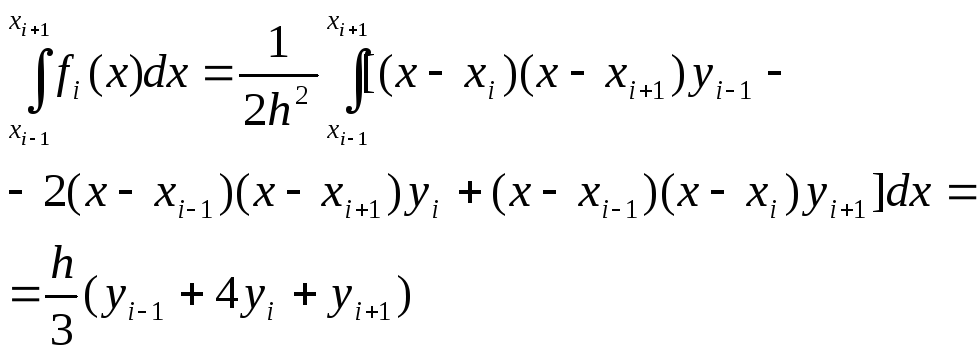
Проведя такие вычисления для каждого из отрезков, получим

(4.13)

4.5 Другие методы численного интегрирования

Квадратурные формулы Ньютона-Котеса получаются путем замены подынтегральной функции интерполяционным многочленом Лагранжа с разбиением отрезка интегрирования на n частей.

Коэффициенты Котеса

При n=1, n=2 формулы Ньютона-Котеса принимают вид формулы трапеций, формулы Симпсона соответственно.

При n=3 (три интервала, 4 точки) формула Ньютона-Котеса называется формулой трех восьмых

Квадратурные формулы Гаусса не предполагают разбиения отрезка интерполирования на равные промежутки. Интерполяционный многочлен (узлы и коэффициенты) подбирают таким образом, чтобы он обладал наивысшим порядком точности при заданном числе узлов интерполирования. Тогда

- так называемые нули полинома Лежандра

- коэффициенты полинома Лежандра

Эти значения табулированы для разного числа узлов.