ЧМ_стац / Численные методы лекции / 9. Необыкновенные дифференциальные уравнения

9. Решение дифференциальных уравнений с частными производными

9.1. Общие сведения

Дифференциальное уравнение с частными производными - это дифференциальное уравнение, содержащее несколько независимых переменных.

Порядок дифференциального уравнения с частными производными – наивысший порядок производной, входящей в дифференциальное уравнение.

Решением является функция, зависящая от нескольких аргументов.

Практическое применение такие уравнения нашли, например, при решении задач механики сплошных сред, в которых в качестве искомых функций обычно служат плотность, температура, напряжение и так далее. Аргументами этих функций являются координаты рассматриваемой точки в пространстве, а также время.

Математическая постановка задачи наряду с дифференциальным уравнением содержит также и некоторые дополнительные условия.

Если решение отыскивается в ограниченной области, то задаются условия на ее границе, называемые граничными (краевыми) условиями. Такие задачи называются краевыми.

Если одной из независимых переменных является время t, то задаются некоторые условия (например, значения искомых параметров) в начальный момент времени t₀, называемые начальными условиями. Такие задачи называются задачами Коши. При этом задача решается в неограниченном пространстве, так как граничные условия не задаются.

Задачи, при формулировке которых ставятся и начальные и граничные условия, называются нестационарными (или смешанными) краевыми задачами. Решения таких задач меняются с течением времени.

Рассмотрим виды дифференциальных уравнений с частными производными на примере дифференциального уравнения с частными производными второго порядка, линейного относительно производных, и двумя независимыми переменными x и y, общий вид которого

(9.1),

- где - искомая функция,

- коэффициенты a, b, c, d, e, f, g, вообще говоря, могут зависеть от переменных х, у и искомой функции .

В связи с этим уравнение (9.1) может быть

1. с постоянными коэффициентами;

2. линейным, если функция g линейно зависит от U, а коэффициенты a, b, c, d, e, f зависят только от х, у;

3. квазилинейным, если коэффициенты a, b, c, d, e, f, g зависят от U.

В зависимости от соотношения коэффициентов уравнение (9.1) может быть:

1) уравнением первого порядка, которое называют уравнением переноса, если

a=b=c=f=0, d≠0, e≠0

(9.2)

Если в этом уравнении вместо х или у выступает время t, то тогда его называют эволюционным уравнением.

2) уравнением второго порядка, если хотя бы один из коэффициентов a, b, c отличен от 0. В зависимости от знака дискриминанта оно может принадлежать к одному из трех типов

- гиперболическому ()

- волновое уравнение (9.3)

- параболическому ()

- уравнение теплопроводности или диффузии (9.4).

- эллиптическому ()

уравнение Лапласа (9.5).

Если в уравнении Лапласа правая часть отлична от 0, то оно называется уравнением Пуассона.

Приведенные уравнения называются уравнениями математической физики.

9.2. Методы решения

Методы решения также как и для обыкновенных дифференциальных уравнений подразделяются на:

- аналитические;

- приближенные;

- графические;

- численные.

Среди численных методов широко распространенными являются разностные методы. Они основаны на введении некоторой разностной сетки в рассматриваемой области. Значения производных, начальные и граничные условия выражаются через значения функции в узлах сетки, в результате чего получается система алгебраических уравнений, называемая разностной схемой. Решая эту систему уравнений, можно найти в узлах сетки значения сеточной функции, которые приближенно считаются равными значениям искомой функции.

Пример простейшей прямоугольной области в двумерном случае показан на рисунке 9.1

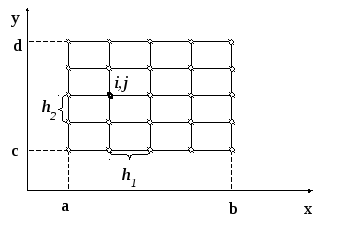
Рисунок 9.1

Стороны прямоугольника делятся на элементарные отрезки точками

Через эти точки проводятся два семейства координатных прямых x=const и y=const, образующих сетку с прямоугольной ячейкой. Любой узел этой сетки определяется координатами ,.

Аналогично вводятся сетки для многомерных областей, содержащих более двух измерений.

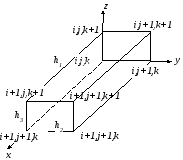
Рисунок 9.2

Элемент сетки в виде прямоугольного параллелепипеда для трехмерной области показан на рисунке 9.2.

Прямоугольные сетки наиболее удобны при организации вычислительного алгоритма. Вместе с тем некоторые схемы используют сетки с треугольными и даже шестиугольными ячейками.

Узлы сетки, лежащие на границе области G, называются граничными узлами, все остальные узлы – внутренними.

Поскольку начальные и граничные условия при постановке задач формируются на границе расчетной области, то их можно считать заданными в граничных узлах сетки.

Иногда граничные точки области не являются узлами сетки, что имеет место для областей сложной формы. Тогда либо вводят дополнительные узлы либо границу приближенно заменяют ломанной, проходящие через близкие к границе узлы.

Например

Преобразование расчетной области можно выполнить путем перехода к новым независимым переменным

К новым переменным нужно преобразовать также дифференциальное уравнение, начальные и граничные условия.

В области G^* можно ввести прямоугольную сетку, при этом в области G ей будет соответствовать сетка с криволинейными ячейками и неравномерно расположенными узлами.

Иногда и в простой расчетной области вводят неравномерную сетку. В частности, в ряде случаев необходимо проводить сгущение узлов для более точного расчета в некоторых частях рассматриваемой области. При этом области сгущения узлов либо известны заранее, либо определяются в процессе решения задачи.

Построим некоторые разностные схемы для решения уравнения теплопроводности при заданных начальных и граничных условиях. Запишем смешанную краевую задачу в виде

где - начальное распределение температуры U (при t=0), , - распределение температуры на концах рассматриваемого отрезка 0,1 в любой момент времени.

Заметим, что начальные и граничные условия должны быть согласованы, то есть

Введем равномерную прямоугольную сетку

, - соответственно размеры (шаги) сетки но направлениям х и t.

Значения функции в узлах сетки обозначим U_i,j.

Заменяя в уравнении теплопроводности частные производные искомой функции с помощью отношений конечных разностей, получим разностную схему

Для этого же уравнения можно построить и другую разностную схему

И в первом и во втором случае получатся система алгебраических уравнений. При этом первая схема называется явной, так как значение определяется через соответствующие значения на предыдущем шаге.

Вторая схема называется неявной, так как каждое разностное уравнение содержит на каждом шаге j+1 значение неизвестных в трех точках, поэтому нельзя сразу определить эти значения через известное решение на предыдущем шаге j.

Эта схема состоит из линейных трехточечных уравнений. Такие системы линейных уравнений с трех диагональной матрицей могут быть решены методом прогонки.

Совокупность узлов при t=const, то есть при фиксированном значении j, называется слоем.

В рассмотренном примере мы получаем двухслойные схемы, когда в каждое разностное уравнение входят значения функции из двух слоев – нижнего, на котором решение уже найдено, и верхнего, в узлах которого решение ищется.

С помощью рассматриваемого способа могут быть также созданы многослойные схемы.