
- •Работа №1. Тема: «Системы счисления»
- •Работа №2. Тема: «Программирование линейных вычислительных процессов»
- •Условие задачи
- •Условие задачи
- •Условие задачи
- •Условие задачи
- •Условие задачи
- •Условие задачи
- •Условие задачи
- •Условие задачи
- •Работа №4. Тема «Программирование разветвляющихся вычислительных процессов»
- •Работа №5. Тема «Изучение математических функций языка С/С++. Особенности функции pow(x,n)»
- •Работа №6. Тема «Программирование циклических вычислительных процессов с варьируемым параметром цикла»
- •Работа №7. Тема «Программирование циклических вычислительных процессов. Сумма ряда»
- •Работа №8. Тема «Программирование циклических вычислительных процессов. Последовательность чисел»
- •Работа №9. Тема «Программирование циклических процессов. Вывод в цикле последовательности символов»
- •Работа №10. Тема «Программирование циклических процессов на языке С/С++ с использованием функций»
- •Работа №11. Тема «Программирование на языке С/С++ с использованием функций. Перевод из одной системы счисления в другую»
- •Работа №12. Тема «Применение функций для решения нелинейных уравнений»
- •Работа № 13. Тема «Обработка одномерных массивов»
- •Работа № 14. Тема «Указатели и динамические массивы. Использование указателей в качестве аргументов функций»
- •Работа № 15. Тема «Обработка двумерных массивов»
- •Работа № 16. Тема «Программирование задач линейной алгебры»
- •Работа № 17. Тема «Структуры в C/С++. Структура комплексное число»
- •Работа № 18. Тема «Применение библиотеки complex.h в С++ при программировании действий с матрицами»
- •Список литературы
Министерство образования и науки, молодежи и спорта Украины Донецкий национальный технический университет
Кафедра вычислительной математики и программирования
ЗАДАНИЯ К ЛАБОРАТОРНЫМ И ПРАКТИЧЕСКИМ РАБОТАМ по курсу «Вычислительная техника и алгоритмические языки» (для студентов специальностей электротехнического факультета)
ДОНЕЦК, 2012
Министерство образования и науки, молодежи и спорта Украины Донецкий национальный технический университет
Кафедра вычислительной математики и программирования
ЗАДАНИЯ К ЛАБОРАТОРНЫМ И ПРАКТИЧЕСКИМ РАБОТАМ
по курсу «Вычислительная техника и алгоритмические языки» (для студентов специальностей электротехнического факультета)
Утверждено за заседании кафедры «Вычислительная математика и программирование»
Протокол №1 от 31 августа 2012 г.
ДОНЕЦК, 2012
УДК 004.43
Задания к лабораторным и практическим работам по курсу «Вычислительная техника и алгоритмические языки» (для студентов специальностей электротехнического факультета) / Алексеев Е. Р., Чеснокова О. В., Кучер Т. В. - Донецк, ДонНТУ, 2012. - 57 с.
Приведены задания к 18 лабораторным и практическим работам по теме программирование на языке С++ курса «Вычислительная техника и алгоритмические языки». В каждой работе приведено по 30 вариантов.
Задания предназначены на студентов специальностей электротехнического факультета младших курсов.
Авторы: |
Алексеев Е. Р., проф., к.т.н. каф. ВМ и П |
|
Чеснокова О. В., ст. пр. каф. ВМ и П |
|
Кучер Т. В., ас. каф. ВМ и П |
Рецензент: |
Толкачев О. Э., доц. каф. ВМ и П |
Содержание |
|
Работа №1. Тема: «Системы счисления» .............................................................................. |
5 |
Работа №2. Тема: «Программирование линейных вычислительных процессов» ............. |
6 |
Работа №3. Тема «Условный оператор в С++. Вычисление значения функции, проверка |
|
попадания точки в область на плоскости» ............................................................................. |
9 |
Работа №4. Тема «Программирование разветвляющихся вычислительных процессов» |
|
.................................................................................................................................................. |
13 |
Работа №5. Тема «Изучение математических функций языка С/С++. Особенности |
|
функции pow(x,n)» .................................................................................................................. |
15 |
Работа №6. Тема «Программирование циклических вычислительных процессов с |
|
варьируемым параметром цикла» ........................................................................................ |
17 |
Работа №7. Тема «Программирование циклических вычислительных процессов. Сумма |
|
ряда» ........................................................................................................................................ |
22 |
Работа №8. Тема «Программирование циклических вычислительных процессов. |
|
Последовательность чисел» ................................................................................................. |
24 |
Работа №9. Тема «Программирование циклических процессов. |
|
Вывод в цикле последовательности символов» ................................................................. |
25 |
Работа №10. Тема «Программирование циклических процессов на языке С/С++ с |
|
использованием функций» .................................................................................................... |
28 |
Работа №11. Тема «Программирование на языке С/С++ с использованием функций. |
|
Перевод из одной системы счисления в другую» ............................................................... |
31 |
Работа №12. Тема «Применение функций для решения |
|
нелинейных уравнений» ........................................................................................................ |
33 |
Работа № 13. Тема «Обработка одномерных массивов» .................................................. |
35 |
Работа № 14. Тема «Указатели и динамические массивы. Использование указателей в |
|
качестве аргументов функций» ............................................................................................. |
36 |
Работа № 15. Тема «Обработка двумерных массивов» .................................................... |
40 |
Работа № 16. Тема «Программирование задач линейной алгебры» ............................... |
43 |
Работа № 17. Тема «Структуры в C/С++. Структура комплексное число» ....................... |
47 |
Работа № 18. Тема «Применение библиотеки complex.h в С++ при программировании |
|
действий с матрицами» ......................................................................................................... |
50 |
Список литературы ................................................................................................................. |
55 |
Работа №1. Тема: «Системы счисления»
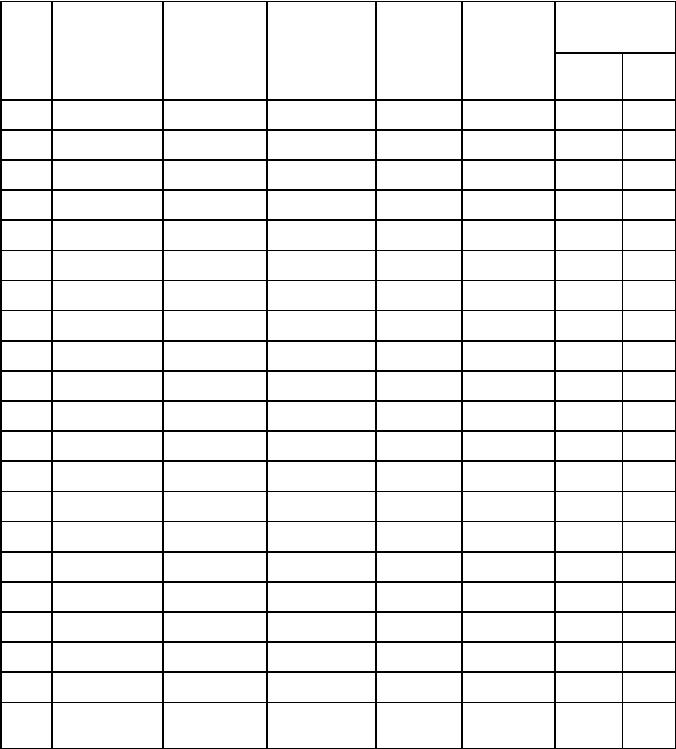
Задание: Выполнить перевод числа из одной системы счисления в другую, сделать проверку (табл.1.1).
Таблица 1.1. Варианты заданий к работе №1
№ |
X2→(?)10 |
Y2→(?)8, |
Z10→(?)2, |
S8→(?)16 |
U16→(?)8 |
Wp→(?)10 |
|
|
|
Y2→(?)16 |
z10→(?)8, |
|
|
Wp |
p |
|
|
|
Z10→(?)16 |
|
|
||
|
|
|
|
|
|
|
|
1 |
11011,1101 |
111101 |
235,647 |
735 |
6D3,2B |
122 |
3 |
2 |
11101,0011 |
110011 |
417,813 |
156 |
95C,F7 |
322 |
4 |
3 |
10101,1111 |
101111 |
176,451 |
376 |
3D6,B5 |
341 |
5 |
4 |
10001,1001 |
100001 |
156,848 |
176 |
63D,C1 |
405 |
6 |
5 |
10011,0001 |
110010 |
601,003 |
641 |
34F,A8 |
501 |
7 |
6 |
11001,1000 |
101000 |
126,012 |
622 |
13A,DE |
608 |
9 |
7 |
11110,1000 |
111000 |
325,632 |
252 |
D13,2B |
271 |
9 |
8 |
10111,0111 |
110111 |
484,191 |
441 |
9E7,2D |
143 |
5 |
9 |
11100,1110 |
101110 |
681,534 |
634 |
3CD,1E |
215 |
6 |
10 |
11000,1010 |
001010 |
183,654 |
134 |
5CA,1E |
306 |
7 |
11 |
10100,1001 |
010001 |
273,021 |
221 |
C3F,E7 |
201 |
3 |
12 |
10010,0101 |
101010 |
289,713 |
271 |
C1F,D5 |
331 |
4 |
13 |
11111,0101 |
110101 |
259,527 |
252 |
986,37 |
320 |
5 |
14 |
10111,1111 |
100111 |
201,113 |
203 |
689,37 |
103 |
6 |
15 |
11111,1101 |
111101 |
114,453 |
153 |
467,EA |
150 |
7 |
16 |
10101,0101 |
100101 |
176,724 |
164 |
ADE,71 |
212 |
3 |
17 |
11010,1001 |
101001 |
106,398 |
632 |
E73,DE |
102 |
4 |
18 |
100010,011 |
100011 |
982,754 |
275 |
D19,AB |
204 |
5 |
19 |
101101,011 |
101001 |
417,98 |
415 |
BE7,D9 |
410 |
6 |
20 |
100111,011 |
100101 |
742,429 |
242 |
1CD,8E |
261 |
7 |
21 |
111011,001 |
110101 |
659,832 |
652 |
5FA,1E |
102 |
3 |
Продолжение табл. 2.1 |
|
|
|
|
|
||
№ |
X2→(?)10 |
Y2→(?)8, |
Z10→(?)2, |
S8→(?)16 |
U16→(?)8 |
Wp→(?)10 |
|
|
|
Y2→(?)16 |
z10→(?)8, |
|
|
Wp |
p |
|
|
|
Z10→(?)16 |
|
|
|
|
22 |
101110,101 |
011101 |
286,327 |
262 |
C38,97 |
232 |
4 |
23 |
111001,011 |
100011 |
687,321 |
672 |
C9F,D5 |
241 |
5 |
24 |
10101,0101 |
101010 |
945,325 |
453 |
9A6,B7 |
451 |
6 |
25 |
110101,100 |
110110 |
467,894 |
674 |
D89,F5 |
653 |
7 |
26 |
10100,1010 |
101101 |
395,532 |
355 |
469,FA |
210 |
3 |
27 |
10111,0111 |
101111 |
984,291 |
421 |
8DE,7A |
302 |
4 |
28 |
110001,110 |
110011 |
671,544 |
614 |
E79,8E |
413 |
5 |
29 |
11010,1111 |
110111 |
883,154 |
354 |
6D8,BA |
305 |
6 |
30 |
111011,001 |
111000 |
473,621 |
476 |
E5C,A4 |
620 |
7 |
Работа №2. Тема: «Программирование линейных вычислительных процессов»
Задание: Написать две программы на языке С/С++ для расчета значений переменных y и z по заданным формулам (табл. 2.1). В первой программе использовать для ввода функцию scanf, для вывода – функцию printf. Во второй программе использовать операторы потокового ввода-вывода cin и cout. Определить разность между значениями y и z. В программе предусмотреть ввод исходных данных. Предварительно вычислить ожидаемые значения y и z с помощью калькулятора. Убедитесь, что значения, вычисленные с помощью калькулятора, совпадают с результатами, которые получаются в результате работы программы.
Таблица 2.1. Варианты заданий к работе №2
|
Вариант 1 |
|
|
|
Вариант 2 |
|
|
|
|||
|
|
sin 2π 3α |
|
|
|
y= cos α+sin α+cos3α sin3α |
|||||
|
|
|
|
|
z= 2 |
|
cosα sin |
π |
2α |
|
|
|
|
|
|
|
2 |
|
|||||
|
y=1 −sin 3α−π |
; |
|
|
4 |
|
|||||
|
|
|
|
|
|
|
|||||
|
z=ctg 54 π+32 α |
|
|
|
|
|
|
|
|
|
|
|
Вариант 3 |
|
|
|
Вариант 4 |
|
|
|
|||
|
y= sin2α sin5α−sin3α |
|
y= sin2α sin5α−sin3α |
|
|||||||
|
|
cos α+1 −2sin2 2α |
|
cos α−cos3α cos5α |
|
||||||
|
z= 2sinα |
|
|
|
z=tg 3α |
|
|
|
|||
|
Продолжение табл.2.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Вариант 5 |
|
|
|
|
|
|
Вариант 6 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
y= 1 −1 sin2 2α cos2α |
|
y= cos α+cos2α cos6α cos7α |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
5 |
|
|
|
|
|
|
||
|
z= cos2 α+ cos4 α |
|
|
|
|
z= |
4cos |
2 |
cos |
2 α cos4α |
|
|
|
|
|||||||||||||||||||||||||
|
Вариант 7 |
|
|
|
|
|
|
Вариант 8 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
2 |
3 |
|
|
α |
|
2 |
11 |
α |
y= 2 sin2 3π−2α cos2 5π 2α |
||||||||||||||||||||||||
|
y=cos |
|
8 |
π−4 |
−cos |
8 π+ |
4 |
|
1 |
|
|
1 |
5 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
sin α |
|
|
|
|
|
|
z= |
4 |
−4 sin 2 |
π−8α |
|
|
|
|
|
|
|||||||||||||||||
|
z= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Вариант 9 |
|
|
|
|
|
|
Вариант 10 |
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
y= cosα−cos β 2− sinα−sin β 2 |
y=cos |
4 |
a+sin |
2 |
2 |
2a−1 |
||||||||||||||||||||||||||||||||
|
z=−4 sin |
2 α−β |
cos α+β |
|
|
|
b+ 4 sin |
|
|
||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
z=sin b+a sin b−a |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Вариант 11 |
|
|
|
|
|
|
Вариант 12 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
1 −2sin2 α |
|
|
|
|
|
|
y= |
|
sin4α |
|
|
cos2α |
|
|
|
|
|
|
||||||||||||||||||
|
y= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 sin3α |
|
|
|
|
|
|
|
1 cos4α |
1 cos2α |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 −tgα |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
π−α |
|
|
|
|
|
|
||||||||||||||||
|
z= |
1+tgα |
|
|
|
|
|
|
|
|
z=ctg 2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
Вариант 13 |
|
|
|
|
|
|
Вариант 14 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
y=sin α+ cos 2β−α |
|
|
y=1 |
sin α+β−γ −sin β+γ−α |
||||||||||||||||||||||||||||||||||
|
|
|
cos α−sin 2β−α |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
1 sin2β |
|
|
|
|
|
|
sin γ+α− β −sin α+β+γ |
||||||||||||||||||||||||||||||
|
z= cos2β |
|
|
|
|
|
|
|
|
z=sin α cos β cos γ |
|
|
|
|
|
|
|||||||||||||||||||||||
|
Вариант 15 |
|
|
|
|
|
|
Вариант 16 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 2x−3 x+1 |
|
x2−9 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
−4 |
|
|
|
|
|||||||||||||||||||
|
y= |
|
|
2b 2 b |
|
|
y= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 2x−3 x−1 x2−9 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
−4 |
+b+ 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
z= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z= |
|
|
|
x+3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
b+2 |
|
|
|
|
|
|
|
|
|
x−3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Вариант 17 |
|
|
|
|
|
|
Вариант 18 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
α+β−γ cos β+γ−α |
|
|
3 tgα−tg3 α |
|
|
|
|
|
|
||||||||||||||||||||
|
y= 4 [ cos |
y= |
|
1 −3 tg2 α |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
cos γ+α−β cos α+β+γ ] |
|
z=tg 3α |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
z= cos α cos β cosγ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение табл.2.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 19 |
|
Вариант 20 |
|
1 −a+a2 −1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 −cosα |
|
|
|
|
|
|
|
|
|
1+a+a2 |
|
|
2 |
|
|||||||||||||||||||||||||||||
y= 1 cosα |
|
y= 2a +a2 2 |
−2a−a2 |
|
5 |
−2a |
|
|
||||||||||||||||||||||||||||||||||||||||
z= |
1 −cosα |
|
z= 4 −a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
sin α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 21 |
|
Вариант 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 tgα−4 tg3 α |
|
|
|
|
|
|
|
|
||||||||||||||||||||
y=8 cos4α 4cos2α 3 |
|
y= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
1 −6 tg2 α+tg4 α |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
z=cos4 α |
|
z=tg 4α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вариант 23 |
|
Вариант 24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
y=1 cos4α−4cos2α 3 |
y=cos α+sin α |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos α−sin α |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
z=sin4 α |
|
z=tg 2α sec2α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вариант 25 |
|
Вариант 26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
y=1 [sin α+β−γ sin β+γ−α |
y=1 3 sin α−sin3α |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
sin γ+α− β −sin α+β+γ ] |
z=sin3 α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
z=sin α sin β sin γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вариант 27 |
|
Вариант 28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
y= |
3m 2 2−24 m |
|
|
|
|
|
y= a |
|
2 |
− |
a |
|
2 |
|
|
|
|
a |
− |
2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
3 |
|
|
− |
2 |
|
|
|
|
|
|
|
|
2a |
|
|
2a 2 |
|
a− 2a |
a 2 |
|
|
|
|||||||||||||||||||||||||
|
m |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
m |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
z=− |
|
|
|
|
|
z= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Вариант 29 |
|
Вариант 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
m−1 m− n−1 |
n |
|
|
|
y=tg α ctg β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
y= |
|
|
|
|
|
|
cos α− β |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
nm m2−m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
m3 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
z= m− n |
|
z =cosα sin β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
