Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Mathematics of Economics and Business.pdf

Скачиваний:

Добавлен:

03.03.2016

Размер:

8.37 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1716 17 > Следующая >>>

Selected solutions

1 INTRODUCTION

1.1

(a) false;

(d)

true; (e)

false

1.2

D : A B C,

E : A

F : A B C,

G : (A

) (

C),

H :

, I :

1.4

(a) A B;

(b)

A B;

(c)

B A;

(d) A B; (e) A B

1.5

(a) true, negation

: x2 − 5x + 10 ≤ 0 is false;

(b)false, negation x2 − 2x ≤ 0 is true

	x
1.8	(a) T, F, F, T; (b) T, F, T, T;	(c) T, T, F, F; (d) F, T, T, T
1.9	A B = {1, 2, 3, 5, 7, 8, 9, 11},	\|A B\| = 8, A ∩ B = {1, 3, 7, 9}, \|A ∩ B\| = 4,
	\|A\| = 6, \|B\| = 6, A \ B = {5, 11}, \|A \ B\| = 2
1.10	subsets: , {1}, {2}, {1, 2}; \|P(P(A))\| = 16

1.134

1.14110 students have a car and a PC, 440 have a car but no PC, 290 have a PC but no car and 840 students have a car or a PC

1.15 A × A = {(1, 1), (1, 2), (2, 1), (2, 2)},	A × B = {(1, 2), (1, 3), (2, 2), (2, 3)},
B × A = {(2, 1), (3, 1), (2, 2), (3, 2)},	A × C = {(1, 0), (2, 0)},

A × C × B = {(1, 0, 2), (1, 0, 3), (2, 0, 2), (2, 0, 3)},

A × A × B = {(1, 1, 2), (1, 2, 2), (2, 1, 2), (2, 2, 2), (1, 1, 3), (1, 2, 3), (2, 1, 3), (2, 2, 3)}

1.16M1 × M2 × M3 = {(x, y, z) | (1 ≤ x ≤ 4) (−2 ≤ y ≤ 3) (0 ≤ z ≤ 5)}

1.17479,001,600 and 21,772,800

1.1856

1.19125 and 60

1.20n2 − n

1.215

1.22(a) 1,128

1.23	(a)		30y − 7x		;	(b)	a2		b2
				2				+2
			6xy + 12y
							2a
1.24	(a)	{x R \| x ≥ −1};								(b) {x R \| (x < 2) (x ≥ 11/4)};
	(c)	{x R \| (x < −1) (0 < x ≤ 2)}; (d)									{x R \| (x < −2) (2 < x < 4)}
1.25	(a)	(−2, 2);		(b)		(1, 5);	(c)		(1/2, 5/2);		(d) (0, ∞); (e) (−1, −1/3]

Selected solutions 487

(a) −19/7;

√

1.26

(b)

9c/b √

1.27

(a)

x = 15;

(b)

x1 =

2, x2 = −

2, x3

= 1,

x4 = −1;

(c)

x1 = −2,

x2 ≈ 19.36,

(x3 ≈ −4.99)

1.28

(a)

a = 2;

(b)

x = 1

1.29

(a)

x = 6;

(b)

x1 = 1,

x2 = 10,

x3 = 0.001;

1.30

(b)

x1 = 2i,

x2 = −2i, x3 = 3i, x4 = −3i

1.31

1.32

z1 + z2 = −1 + 5i,

z1 − z2 = 3 + 3i,

z1z2 = −6 − 7i,

1.33

(a)

(z) = 0,

(z) = −1,

z = −i;

(b)

(z) = −1,

(z) = 0,

z = −1;

(c)

(z) = −√

(z) = −3, z = −√

− 3i

1.34

(a)

z = −i = 1(cos 23 π + i sin 23 π ) = e3π i/2;

(b)

z = −1 = 1(cos π + i sin π ) = eπ i;

(c)

z = 3(cos 60◦ + i sin 60◦) = 3eπ i/3

;

(d)

z = √

(cos 243◦ + i sin 243◦) = √

· e4.25i

1.37

(a)

z1 = √

+ i,

z2 = −1 + √

z3 = −√

− i,

√

3 − i),

(b)

z1 = 2 i,

z2 = 4 (−

= 4

(

3 − i)

1.38

a1 = −32,

a2 = 1

2 SEQUENCES; SERIES; FINANCE

z1 = 2 − 9 i z2 5 5

z4 = 1 − √3 i;

2.1	(a)	a101 = 815;	(b) d = 2, a1 = 7, an = 2n + 5
2.2	(a)	strictly increasing		(b) unbounded;			(c)	an+1 = an + 1/2
2.3	(a)	a1 = 3, n = 16;		(b)	a1 = 18,		q = 1/3
2.4	{an} is strictly decreasing and bounded,					nlim		an = −5;
	{bn} is not monotone but bounded,				nlim		→∞
	{bn} is not monotone but bounded,				nlim		bn = 0;
	{cn} is decreasing and bounded,				→∞
	{cn} is decreasing and bounded,				nlim cn = 0
					→∞

488	Selected solutions
2.5	(a)	nlim	an = 2/e;
		→∞					−∞	for	a < 0
							−∞	for	a < 0
	(b)	nlim	bn		=		1/3	for	a = 0	;
		→∞			=		∞	for	a > 0
	(c)	lim	c	n	=	0	(both for c1 = 1 and c1 = 4)
	(c)	n→∞		n	=		(both for c1 = 1 and c1 = 4)

2.6(a) shirts: a1 = 2, 000; a2 = 2, 500; a3 = 3, 000; a10 = 6, 500; trousers: a1 = 1, 000; a2 = 1, 200; a3 = 1, 440; a10 = 5, 159.78;

(b)shirts: s15 = 82, 500; trousers: s15 = 72, 035.11

2.7	(a)	s = −10/7;	(b)	s = 1
2.8	(a)	series converges for −1 ≤ x < 1;						(b) series converges for \|x\| > 1
				92		, s4		= −	157
2.9	(a)	s1 = −12, s2 = −8, s3 = − 9				, s4		= −	18 ,	series converges;
		s1 = 1, s2 = 3, s3 =		9	31
	(b)	s1 = 1, s2 = 3, s3 =		2 , s4 =		6	,	series converges;
		1	113	113			39			416
	(c)	s1 = 2 , s2 =	162 , s3	= 162 +			49 , s4 = s3 +				, series converges;
	(c)	s1 = 2 , s2 =	162 , s3	= 162 +			49 , s4 = s3 +			516	, series converges;
		s1 = 0, s2 =	3	5		25
	(d)	s1 = 0, s2 =	2 , s3 =	6 , s4 =		12 ,		series does not converge.
2.10	(a)	17, 908.47 EUR; (b)		17, 900.51 EUR;					(c) 18, 073.83 EUR; (c) is the best.

2.1149, 696.94 EUR

2.12interest rate i = 0.06

2.13 (a)	Aannually = 16, 288.95 EUR; Aquarterly = 16, 436.19 EUR;
	Amonthly = 16, 470.09 EUR;
(b)	ieff −quarterly = 0.050945; ieff −monthly = 0.051162

2.145,384.35 EUR

2.15 (a)	bank A: 2, 466 EUR;	bank B: 2, 464.38 EUR
(b)	bank A: 2, 478 EUR;	bank B: 2, 476.21 EUR

2.16(a) sinking fund deposit: 478.46 EUR;

(b)sum of interest and deposit: 550.46 EUR

2.171, 809.75 EUR

2.18	(a)	V1 = 62, 277.95 EUR;	(b)	V2 = 63, 227.62 EUR
2.19	(a)	A = 82, 735.69 EUR;	(b)	P120 = 58, 625.33 EUR
2.20	(a)	P = 22, 861.15 EUR;	total payment 228, 611.50 EUR

Redemption table for answer 2.20(a) (EUR)

Period	Annuity	Amortization	Interest	Amount of the
(year)		instalment		loan at the end

1	22,861.15	10,111.15	12,750.00	139,888.85
2	22,861.15	10,970.59	11,890.55	128,918.25
3	22,861.15	11,903.10	10,958.05	117,015.15
4	22,861.15	12,914.86	9,946.29	104,100.29
5	22,861.15	14,012.62	8,848.52	90,087.66
6	22,861.15	15,203.70	7,657.45	74,883.96
7	22,861.15	16,496.01	6,365.13	58,387.95
8	22,861.15	17,898.17	4,962.97	40,489.77
9	22,861.15	19,419.52	3,441.63	21,070.25
10	22,861.15	21,070.18	1,790.97	0.07

Selected solutions 489

(b)total payment: 220,125.00 EUR

Redemption table for answer 2.20(b) (EUR)

Period	Annuity	Amortization	Interest	Amount of the
(year)		instalment		loan at the end

1	27,750	15,000	12,750	135,000
2	26,475	15,000	11,475	120,000
3	25,200	15,000	10,200	105,000
4	23,925	15,000	8,925	90,000
5	22,650	15,000	7,650	75,000
6	21,375	15,000	6,375	60,000
7	20,100	15,000	5,100	45,000
8	18,825	15,000	3,825	30,000
9	17,550	15,000	2,550	15,000
10	16,275	15,000	1,275	0

2.21 (a) the project should not go ahead; (b) 1 per cent, 2 per cent; (c) yes

2.22(a) depreciation amount in year 1: 7,000 EUR, in year 8: 7,000 EUR

(b)depreciation amount in year 1: 12,444.44 EUR, in year 8: 1,555.55 EUR

(c)depreciation amount in year 1: 9,753.24 EUR, in year 8: 4,755.21 EUR

3 RELATIONS; MAPPINGS; FUNCTIONS OF A REAL VARIABLE

3.1 (a)	R:
5							1	1
5							1	1
4									2
4							2		2
3							3		3
3							3		3


2							4		4
2							4		4
1							5
1							5	5

		1	2	3	4	5

(b)T, F, F, F;

(c)R−1 = {(2, 1), (4, 1), (1, 3), (4, 3), (5, 3), (1, 5), (4, 5)};

(d)R: no mapping; S: mapping

3.2	(a)	bijective mapping,				(b) surjective mapping,
	(c)	mapping, (d)		injective mapping
3.3	(a)	Illustration by graphs:
	f :			g:				f ◦ g:
	f :							f ◦ g:
	1 1			2			1	2		1			1
	1 1			2			1	2		1			1

				3				3
	2		2	3			2	3			2		2
	3		3				3				3	3
	(b)	Df = A, Rf = B;			Dg = C, Rg = {1, 2} A; Df ◦g						= Rf ◦g	= C B;
	(c)	f : bijective,		g: injective, f ◦ g: injective,					g ◦ f : no mapping

490	Selected solutions
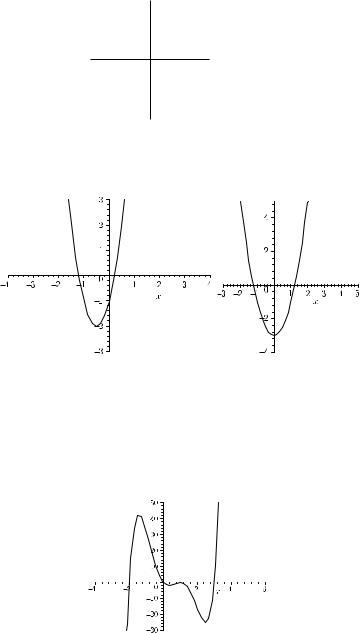
3.4	F −1 is a mapping with domain DF −1 = R and range RF −1 = [−2, ∞).
						F
	F −1	4
		3
		3					F	−1
		2


		1
	-4 -3	-1				3 4
	-4 -3	-2 -1		1 2		3 4


		-2
		-3


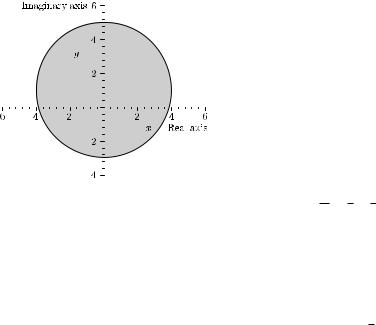
3.5	F is a function, F −1 exists.					F
	G is not a function, y = ±√				is an ellipse with midpoint (0, 0) and a =				√
	G is not a function, y = ±√		9 − 4.5x2		is an ellipse with midpoint (0, 0) and a =				√	2,
	b = 3.							(f ◦g)(x) = 2x2 − 3
3.6	(g ◦f )(x) = 4x2 + 4x − 1							(f ◦g)(x) = 2x2 − 3

3.7

(a)

f and g bijective; (b) f −1(x) = ln x, g−1(x) = −x;

(c)

f ◦g = e−x ,

g ◦f = −ex

f −1(x) = −1 + √

3.8

a = −1,

Rf = {x R | −4 ≤ y < ∞},

4 + x

3.9

(a)

= {x R | x ≥ 0},

2 Rf = {y R | − 1 ≤ y < 1};

f −1 : y = 16 · (x + 1)2 , −1 ≤ x < 1;

(b)

= R,

(x − 1)

f −

y =

Rf = R,

√x + 2

3.10

(a)

(P5/P2)(x) = 2x3 − 2x2 − 12x;

(b)

P5(x) = (x − 1)(x − 1)(x + 2)(x − 3)2x

(d)

Selected solutions 491

3.11

x1, x2, x4 are zeroes; x3 is not a zero;

f (x) = (x − 1)(x + 1)(x + 1)(x + 2) x − 21 (1 +

√

i) x − 21 (1 − √

3.12

(a) f1

: Df1

= R, Rf1

= [−1, 1], odd;

Df2

= R, Rf2

= [−2, 2], odd;

: Df3

= R, Rf3

= [−1, 1], odd;

Df4

= R, Rf4

= [1, 3];

f5 : Df5

= R, Rf5

= [−1, 1];

(b)f1 : Df1 = R, f3 : Df3 = R, f5 : Df5 = R,

Rf1 = {x R : x > 0}; f2 : Df2 = R, Rf2 = {x R : x > 0}; Rf3 = {x R : x > 0}; f4 : Df4 = R, Rf3 = {x R : x > 2}; Rf5 = {x R : x > 0}

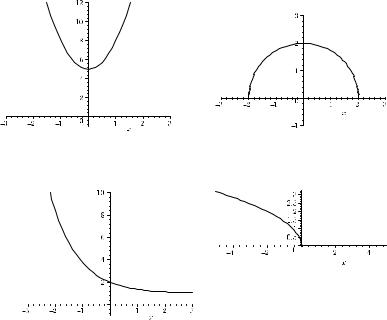
3.13 (a) Df = {x R \| x = 0}, Rf = R,			(b) Df = {x R \| x > 0}, Rf = R,
	f	unbounded and even,		f	unbounded,
	f	strictly decreasing for x < 0,		f	strictly increasing
	f	strictly increasing for x > 0

492 Selected solutions
(c) Df = R, Rf = {y R \| y ≥ 5},		(d) Df		= {x R \| \|x\| ≤ 2},
f bounded from below and even,		Rf		= {y R \| 0 ≤ y ≤ 2},
f	strictly decreasing for x ≤ 0,	f	bounded and even,
f	strictly increasing for x ≥ 0	f	strictly increasing for x ≤ 0,
		f	strictly decreasing for x ≥ 0

(e) Df = R, Rf = {y R \| y > 1},		(f) Df = R, Rf = {y R \| y ≥ 0},
	f bounded from below,	f bounded from below,
	f strictly decreasing	f decreasing

4 DIFFERENTIATION

4.1

(a)

lim

(b)

lim f (x)

x→x0 f (x) = a;

x→1

(c)

lim

(d)

lim

0 f (x) =

lim

0 f (x) = 1

→

0 f (x) = 0;

−

→

4.2

(a)

lim x3 − 3x2 + 2x

2, gap;

→

−

(b)

lim

x3 − 3x2

= ∞

lim x3 − 3x2

= −∞

pole;

−

→

−

→

(c)lim x3 − 3x2 = −∞, pole

x→2 (x − 2)2

4.3 (a) f (2) not defined, x0 = 2 gap; (b) continuous; (c) jump; (d) jump

4.4(a) not differentiable at x0 = 5, differentiable at x1 = 0;

(b)differentiable at x0 = 0, not differentiable at x1 = 2

6x2

−

(x4

4.5 (a)

3 cos x;

(b)

(4x3

4) sin x

4x) cos x;

(c)

= 4x + 2x sin x + 2 sin x + sin

−

cos x

;

y = 4(2x

(2 + sin x)

(d)

(6x

− 3x + ln x)

− 3 + x );

Selected solutions 493

(e)y = −4(x3 + 3x2 − 8)3(3x2 + 6x) sin(x3 + 3x2 − 8)4;

(f)y = −4(3x2 + 6x) cos3(x3 + 3x2 − 8) sin(x3 + 3x2 − 8);

ex cos ex

y =

(g)

√

;

(h)

+ 1

sin e

2/3

1/3

4.6

(a)

y = sin x + cos x;

(b)

;

(c)

y =

3 (x−

+ x−

)

cos x

4.7

(a)

f (x) = ln(tan x) +

;

(tan x)

sin x cos x

(b)

−

cos(x

−

);

f (x) = ln x + 1 − x

x + 2 + 2(x − 1)

− x

− x − 2

x3(x − 2)2

(c)

(x)

2)√x −

4.8

(a)

f (x) = 6 cos x − 6x sin x − x2 cos x;

(b) f (x) =

;

(c)

f (x)

= −

x2 + 12x + 12

;

(d) f (x)

4)ex

−

2)6

4.9

exact change: 28;

approximation: 22

4.10

−10

4.11

f (x) = 2

;

g (x)

;

εf (x) =

2 x;

εg (x) =

2 ;

f (1) = f (100) =

;

g (1) =

; g (100) =

200

Function f is inelastic for x (0, 2) and elastic for x > 2;

function g is inelastic for

x > 2.

When f

changes from x0

= 1 to 1.01, the function value changes by 0.5 per cent;

when f

changes from 100 to 101, the function value changes by 50 per cent.

When g changes from some x0 by 1 per cent, the function value always changes by

0.5 per cent.

4.12

εD ( p) = −4( p − 1)p;

demand D is elastic for p > (1 + √

)/2 and inelastic for 0 < p < (1 + √

)/2;

p = 1/2 (εD (1/2) = 1)

4.13

(a)

local minima at P1 : (0, −5) and P2 : (2, −9),

local maximum at P3 : (0.25; −4.98),

global maximum at P4 : (−5; 1, 020);

(b)

global maximum at P1 : (3, 4),

global minimum at P2 : (−5, −4);

(d)

local minimum at P1 : (4, 8),

local maximum at P2 : (0; 0),

global maximum does not exist;

(e)global minimum at P0 : (0, 0),

global maximum at the endpoint of I , i.e. P1 : (5, 0.69)

4.14local minimum at P1 : (1, 5/6), local maximum at P2 : (2, 2(2 − ln 2)/3 for a = −2/3, b = −1/6

4.15	(a)	1;	(b) 1/4;	(c)	1; (d) 1; (e) 1/6;	(f)	−1/6
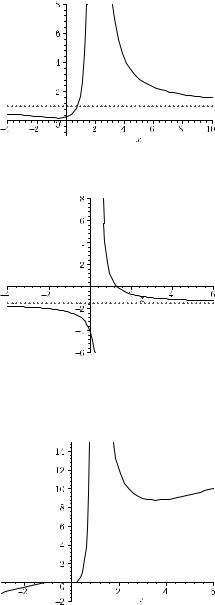
4.16	(a)	Df	= R\{2},	no	zero, discontinuity at x0	= 2,	local minimum at P1 :
		(−1/2, 1/5), inflection point at P2 : (−7/4, 13/45), x					lim f (x) = 1, f strictly
							→±∞

494 Selected solutions

decreasing on (−∞, −1/2] (2, ∞), f strictly convex for x ≥ −7/4

(b)	Df = R\ {0, 1/2},		zero: x0 = 4/3, discontinuities: x1 = 0 and x2 = 1/2,
	x lim f (x) = −3/2, f strictly decreasing on Df ,			f strictly convex for x > 1/2
	→±∞
(c)	Df = R\{0; 1},	zero: x0 = −1, discontinuities: x1			= 0 and x2 = 1, local
	minimum at P3	: (3.56, 8.82), local maximum at P4			: (−0.56, 0.06), inflec-
	tion point at P5	:	(−0.20, 0.02), x lim f (x)	= −∞, xlim f (x) = ∞, f
			→−∞		→∞
	strictly decreasing on [−0.56, 0) (1, 3.56], f			strictly convex for x ≥ −0.2

(d) Df (x) = R, no zeroes, local maximum at P1 : (2, 1), inflection points at

P2	: (1, e−1), P3	: (3, e−1), x	lim f (x) = 0, f strictly increasing on (−∞, 2],
			→±∞

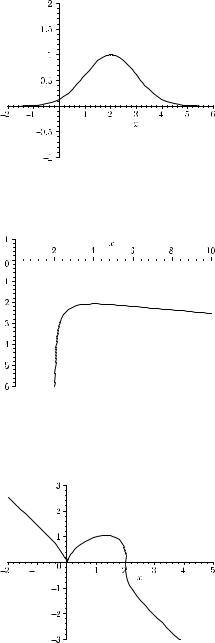
Selected solutions 495

f strictly concave for 1 ≤ x ≤ 3

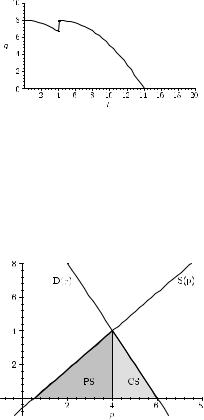
(e) Df = {x R \| x > 2},			no zero, local maximum at P1 : (4, −3 ln 2), inflection
	point at P	2 : (6.83, −2.27), xlim f (x) = −∞, x		2 0 f (x) = −∞, f strictly
	decreasing for x ≥ 4, f		→∞	→ +
	decreasing for x ≥ 4, f		strictly convex for x ≥ 6.83

(f) Df (x) = R, zeroes: x0 = 0, x1 = 2, local minimum at P2 :				(0, 0), local
maximum at P3	: (1.33, 1.06), inflection point at P4	: (2, 0), x	lim	f (x) = ∞,
			→−∞

lim f (x) = −∞, f strictly decreasing on (−∞, 0] (4/3, ∞), f strictly convex

x→∞

for x ≥ 2

496

Selected solutions

4.17

(a) f (x) = 1 −

π 2

− 2)

π 4

− 2)

+ R5

32 (x

6144

π 6

· sin

+ λ(x − 2))

2)6

R5 = − 46

−6!

0 < λ < 1;

(b)f (x) = x − x22 + x33 − x44 + − . . . + (−1)n−1 · xnn + Rn,

Rn = (−1)nxn+1 , 0 < λ < 1;

+1)(λx + 1)n+1(n

(c) f (x) = 2x − 2x				2	−	1	3	+ x	4	+ R4	,
						3 x
R4 =	x5	· e−	λx	[−41 sin(2λx) − 38 cos(2λx)], 0 < λ < 1
	5!

4.18T4(− 15 ) = 1 + (− 15 ) + 21! (− 15 )2 + 31! (− 15 )3 + 41! (− 15 )4 = 0.81873

4.19(a) Newton’s method

f (xn)

−3

−6

0.333333

+0.037037

−5.66667

0.339869

+4.29153 · 10−5

−5.65347

0.339877

+4.29153 · 10−5

−5.65347

(b)

regula falsi

f (xn)

−3

0.4

−0.336

0.342466

−0.146291

0.339979

−0.000577

0.339881

−0.000023

0.339877

−9.536 · 10−7

4.20

Newton’s method

f (xn)

0.3905620

4.5117973

0.0051017

4.5052428

0.0000010

4.505241496

1.6 · 10−10

5 INTEGRATION

5.1

(a)

sin x

+ C;

(b)

(ln x)

+ C;

(c)

−

− 4x| + C;

(d)

+ C;

4 ln |1

2 e−

√

(e)

+ 1

+ C;

(f )

1(x

− 2) + C;

(g)

2 ln(e

+ 1) − 2 arctan e

+ C;

(h)

3 arcsin

√

+ C;

Selected solutions 497

− sin x + C;

(j) −

(i)

−

+ C;

sin x

tan 2x

(k)

2 tan2

+ C

tan

−

2 e (sin x

5.2 (a)

e (x

(b)

cos x)

(c)

x tan x + ln | cos x| + C;

(d)

(cos x sin x + x)

+ C;

x ln(x2 + 1) − 2x + 2 arctan x + C

(e)

ln x −

(f )

5.3 (a)	3; (b)	4 − 2 ln 3;	(c)	2/3;	(d) 10/3;
	1	− 1\|; (f )
(e)	2 ln \|2t	− 1\|; (f )	1/3;	(g)	π/4

5.4(a) total cost C = 9, 349.99; total sales S = 15, 237.93; total profit P = 5, 887.94

(b) average sales Sa = 3, 809.48; average cost Ca = 2, 337.49;

(c)P(t) = 10, 000e−t (−t2 − 2t − 2) + 20, 000 − 1, 000(4t − 2 ln (et + 1) +2, 000 ln 2

5.5	(a)	4;	(b) A = 32.75
5.6	(a)	graph for q0 = 8, t0 = 4:

q0T 1 − T

12T

x = T /2

(b)

− 300

;

(c)

5.7

(a)

0.784981;

(b)

0.783333;

(c)

0.785398;

exact value: π/4

5.8

(a)

(b)

1/2;

(c)

1 ;

λ > 0

;

(d)

2/λ2;

λ > 0

0 ;

λ = 0

0 ;

λ = 0

−∞ ;

λ < 0

−∞ ;

λ < 0

(e)

(f )

does not exist

5.9

1,374.13

5.10

PS = 7;

CS = 4.

498 Selected solutions

VECTORS

−

6.1

(a) a

−9

−7

−5

−11

	b − 4a + 2c =			−4		,	a + 3(b − 2c) =	−23	;
					−3			−7
	a > b,				c >
(b)		c	a,		14	b;		−43
(c) aT · b = 0,			≥ aT · c = 0,				bT · c = −18;
	a,b orthogonal;			a,c orthogonal; (b, c) ≈ 126.3◦
				0			−36

(d)(aT · b)c = 0 , a(bT · c) = −18 ;

(e)

|b + c| = √

|b| + |c| =

√

|bT · c| = 18, |b||c| =

√

29,

44,

6.2

α = β − 2,

β R

6.3

(a)

√

19;

M = {(a1, a2) R2 | a1 ≥ b1 a2 ≥ b2};

(b)

a ≥ b :

|a| ≥ |b| : M = {(a1, a2) R2 | a21 + a22 ≥ b21 + b22}

6.4all the vectors are linear combinations of a1 and a2; (0, 0.5)T is a convex combination

6.5a4 = 12 a1 + 14 a2 + 14 a3.

6.6	no
6.7	no; no basis
	5
	5
	4
	3
	2
	1

	-4 -3 -2 -1		3 4 5
	-4 -3 -2 -1	1 2	3 4 5

6.8yes

Selected solutions 499

	3	=		1	+		0	+		1
6.9 (a)	−3		0	3		3	0		3	−1
	3			0			1			0	;

(b)bases: a, a1, a2 and a, a1, a3;

(c)b = 2a1 − a2 + a

7MATRICES AND DETERMINANTS

7.1	(a)			AT =								4						2						,		no equal matrices;
												1				−2
																6				5					1				− D =							0				3				1		,
	(b)			A + D =												5				4					0 ,			A	− D =							−3				0 −4						,
						− =											2							2					− = − − −
																	1							0													2				1					1
				AT				B														−		0				9		1					2	−5				−1				−1
				AT				B						3										0		, C D										−5				−1				−1
					+		3(BT						−								= −20 −4 −14
	(c)			A			3(BT									2D)											−						−
							2								0						1.5									0				1		−1.5
7.2	A						0								1				−0.5											1		−0 −0.5
		=			1.5					−0.5											−2					+			1.5			0.5							0
7.3	(a)		AB =									26				32							0			;		(b)		AB =						45				51				58			;
7.3	(a)		AB =									23				27							1			;		(b)		AB =						25				18				32			;
	(c)		AB			=		10;																						BA		=				−6					−9				−12					−15
						=																										=				−4					−6				−			8		−10
																																				12					18						24			30		;
																																					6					9					12			15
						=																										=					6					3						9
	(d)		AB									0				0					;									BA				−2							−1				−			3	;
	(d)		AB			=						0				0					;									BA				−2							−1				−			3	;
						=							x+5y+2z																												−
	(e)		AB									2x+3y+ z																													−
				=							3						6						·						−			=								12					3				9		=
	ATBT										2						4										2	1			1										8				2				6			(BA)T,
7.4																−											3	2			4						−							−1				−3
7.4						−1										−2											3	0	−2										−4					−1				−3
				=				2					1			−						·						3			6			=			0				0		=
								2					1						1										−								0				0
	BTAT							3 0								−2										−1			−2								0 0									(AB)T
7.5	(a)		ACB = D(3,1),														−																				−1
																				2							0	1			0						−1													2
	(b)		(AC)B																						−12			7	−24										2
																−																							0
									=							−14							0																0						−178						,
																1		10					0				9	5			18							2											154
																		10									9	5			18				·				7		=								154
			A(CB)													7				−4								2
																												48
									=																			48					−178
									=							5							3				·		=							154

500	Selected solutions
			=	0	0	14	46			=		0		0	0	70			=		≥
7.6	(a)	A2	=	0 0 0			0		A3	=		0	0 0 0					Ak	=	0, k	≥	4;
7.6	(a)	A2		0	0	0	35	,	A3			0		0	0	0	,	Ak		0, k		4;

				0	0	0	0					0		0	0	0
				0	0	0	0					0		0	0	0
	(b)	B2k = I ,			k N ;		B2k −1 = B;				k N

7.7(a) R1: 74,000 units and R2: 73,000 units;

(b)31 EUR each unit of S1, 29 EUR each unit of S2 and 20 EUR each unit of S3; 275 EUR for F1 and 156 EUR for F2.

−1 4 2 0

7.8(a) A12 = 0 1 , A22 = 0 1 ;

(b)	\|A12\| = −1, \|A22\| = 2;
(c)	cofactor of a11: −18, cofactor of a21: −3, cofactor of a31: 12;

(d)|A| = −33

7.9	(a)	−6,	(b) 5,	(c) 70,	(d) 8, (e) 0, (f ) (−1)n−13n
7.10	(a)	x = 2;	(b)	x1 = −2,	x2 = 0
7.11	x1 = 2, x2 = 3,			x3 = −5

7.12the zero vector is the kernel of the mapping

−1

→ u3

−14

−10

7.13

−1

		−1/11	3/11	−3/11	;			1	−3/2	8	;
7.14 (a) A−1		−4/11	1/11	10/11	;	(c) C−1		0	1/2	−2	;
	=	4/11	−1/11	1/11			=	0	0	−1

	(d)		D−1						2			−1			−1			1
	(d)		D−1						0			1/2				1	−1/2
						=					−				−
						=			5		−	−4			−			2
					0				2			3/2				1	1/2
		1			0			−1 −2 −9									−16
						1			2			5		21			41
						0			0			0			0		−1
7.15	A−		=			0			0			1			3		5
7.15	A−		=			0			0			0			1		−2

												17
			−		=		−	−			=	17			−7 −12
7.16	(AB)			1		B		1A		1			1		−23 −37
7.16	(AB)			1		B		1A		1					−23 −37
7.17	(a)		X = BTA−1;										(b)		X = B(A + 2I )−1;						(c) X = A−1CB−1;
	(d)		X = C−1AB−1;												(e)		X = [(A + 4I )CT]−1
7.18	(b)		x −→ (I − A)x = y;													(c)		no;		(d)	y R4 −→ x = (I − A)−1y R4
7.19	(a)		q = (I − A)p											0	3		0	0	1
														0	3		0	0	1
														0	0		0	0	5
														0	0		0	2	0
			with A = (ai,j ) =											0	0		0	2	0	;
			with A = (ai,j ) =											0	0		0	0	2	;


														0	0		0	0	0

Selected solutions 501

(b)p = (I − A)−1q;

(c)	r = Bp = B(I − A)−1q											1	3	0	0	16
	= =			0	0	0	0	7		− =		1	3	0	0	16
	= =			0	0	0	0	7		− =		0	0	0	1	2
				1	0	3	0	0				0	1	0	0	5
										A)−1		0	0	0	0	1
	with B	(bij )		5	1	0	0	0	, (I	A)−1		0	0	1	2	4	,
	rT = ( 660,		1740,		70	)
8 LINEAR EQUATIONS AND INEQUALITIES
8.1 (a)	x1 = 1,	x2 = 2,		x3 = 0;			(b)	no solution;			x3 = 1
(c)	no solution;						(d)	x1 = 5,		x2 = 4,	x3 = 1

8.2(a) (i) x1 = x2 = x3 = x4 = 0;

(ii)

x1 = −9t, x2 = 11t, x3 = −3t, x4 = t,

t R;

(b) (i)

x1 = 3,

x2 = −3,

x3 = 1,

x4 = −1;

x4 = t,

t R

(ii)

x1 = −6 − 9t,

x2 = 8 + 11t,

x3 = −2 − 3t,

x1 = 5 + 3t,

x2 =

= t, t R;

8.3

(a)

2 −

2 t, x3 =

2 +

2 t,

x1 = 2 +

t, x2 = 5 −

t, x3

= t, x4 = −1 +

t, t

(b)

x1 = 4 − 3t1 − 2t2,

x2 = −1 + 2t1 − t2,

x3 = t1,

x4 = 1 + 3t2, x5 = t2;

x1 = 6 + 2t1 − 7t2, x2 = t1, x3 = t2, x4 = −2 − 3t1 + 6t2,

x5 = −1 − t1 + 2t2;

t1, t2 R

8a − 46

−3a + 12 , z

8.4

31 : x

, y

−

= 6a

−

= 6a

8.5the cases ‘no solution’ and ‘unique solution’ do not exist for any λ.

λ = 2 :	x = −	1	2
		3 z −	3 y, y, z R;
λ = 2 :	x = −	2	y R; z = 0
		3 y,

8.6 (a)	no solution for: a = 0, b R		or a = −1/3, b = 1;
	unique solution for: a = 0, b = 1;
	general solution for: a = −1/3, b = 1
(b)	x1	= 2 + t, x2 = −t, x3 = −3,	x4 = t, t R;
(c)	x1	= 6, x2 = 0, x3 = 1, x4 = 4

8.7	x = 1,	y = 2,	z = 3	t R,
	x = 1,	y = t,	z = 5 − t,	t R,
	x = 4 − t,	y = 2,	z = t,	t R,
	x = −2 + t, y = 2,		z = t,	t R,

for a = 0, |a| = |b|; for a = 0, b = 0; for a = 0, a = b; for a = 0, a = −b

8.8 ker(A) = (−3t/2, −t/2, t)T , t R

8.9system 1: x1 = 1, system 2: x1 = 5,

8.10 (a) A−1	=	4
		1
		−1

= 2,

x3 = 0;

= 0,

x3 = 3

− =

−4

−3

−1

; (c)

−

1/2

−

−1/2

3/2

1/2

502	Selected solutions										=	5	− 2 −1
			=	9	−11 −52 −40						=	5	− 2 −1
8.11	(a)	X		1	−6	78		51	;	(b) X		1	11 8	;
		X =			10	10	2
	(c)	X =			−15	−11	−1
8.12	(b)	X			5.79	17.80			14.19	10.18
8.12	(b)	X		28.99		29.67			9.46	30.54

					11.59	23.73			18.52	20.36
			= 11.59			35.60			14.19	25.46

8.13a belongs to the set; b does not belong to it.

8.14(b)

= λ1

+ λ2

200

+ λ3

+ λ4

100

(c)

240

200

λi = 1,

λi ≥ 0,

i = 1, 2, 3, 4;

i=1

8.15

x2	= λ1	0	+ λ2	3	+ λ3	5	+λ4	0	+ µ1	1	+ µ2	1 ,
x1		0		0		1		1		1		2

4		λi ≥ 0,		i = 1, 2, 3, 4,			µ1, µ2 ≥ 0
λi = 1,		λi ≥ 0,		i = 1, 2, 3, 4,			µ1, µ2 ≥ 0

i=1

Selected solutions 503

3/4

5/9

8.16 (a)

λ1

λ2

λ3

λ4

7/9

λi = 1, λi ≥ 0, i

= 1, 2, . . . , 6;

+λ5 11/7

+ λ6 1

10/7

i=1

+ λ3

+ λ4

(b)

λ1

λ2

12/5

0 +

3/5

λi ≥ 0,

i = 1, 2, . . . , 5

+ λ5

λi = 1,

3/5

i=1

9 LINEAR PROGRAMMING

9.1 (a)

(b)

(c)infinitely many solutions

9.2	z	=	10x1	+	6x2	→	max!
			x1			≤	100
			−3x1	+	x2	≥	30
			−3x1	+	x2	≤	0
			x1	+	4x2	≤	200
					x1, x2	≥	0

(d)	no optimal solution

504 Selected solutions

optimal solution: x1 = 80, x2 = 30; z = 980

9.3

(a)

z¯ = −z = −x1 + 2x2 − x3 → max!

s.t.

+ x5

≥

−3x1

+ x2

− x3

= 4

j = 1, 2, 3, 4, 5

(b)

= −

−

2x2

3x3

−

→

max!

¯ = −

s.t.

−

1 x3

3 x

−

3 x

2 4

−

2x3

−

2x3

−

, x

x , x2

, x3, x

, x5, x6, x7

≥

9.4

(a)

x1 = 8/5,

x2 = 3/5;

z = 11/5;

(b) infinitely many optimal solutions: z = −11;

+ (1

− λ)

, 0 ≤ λ ≤ 1

x = λ 5

9.5

(a)

x1 = 0,

x2 = 10,

x3 = 5,

x4 = 15;

z = 155;

(b) a (finite) optimal solution does not exist;

9.6 x1 = 80, x2 = 30, x3 = 20, x4 = 0, x5 = 210, x6 = 0; z = 980;

9.7(a) a (finite) optimal solution does not exist;

(b)z = 24;

x1	=		5.5	+		−		10			≤		≤
x3			9.5		(1			14		0				1
x2		λ	4.5				λ)	0	,			λ

(c)the problem does not have a feasible solution.

9.8dual problem of problem 9.5 (a):

w = 400u5 + 30u6 + 5u7 → min!
s.t. 20u5	+	u6	≥	7
10u5	+	u6	≥	4
12u5	+ u6		+ u7 ≥ 5
16u5	+	u6	≥	6

uj ≥ 0; j = 5, 6, 7

dual problem of problem 9.7 (a):

w = 10u5 + 4u6 → max!

s.t	−3u4	+	u5	+		≤	1
	u4	+ 2u5		+	u6	≤ 1
	4u4	+		+	3u6	≤	−1
uj	≥ 0; j = 4, 5, 6

Selected solutions 505

dual problem of 9.7(c):
w = 4u5 + 9u6 + 3u7 → min!			≥
s.t. u5	+ 2u6	+ u7	≥	2
u5	+ 3u6	+ u7	≥ −1
−u5	− u6	+ 2u7	≥ 1
−u5	− 2u6		≥	0

u5 R; u6 R; u7 ≤ 0

9.9(a) primal problem: x1 = 0, x2 = 9/2, x3 = 1/2, x4 = 17/2; z = −18; dual problem: u5 = 1, u6 = 4, u7 = 1; w = −18;

(b)primal problem: x1 = 17, x2 = 0, x3 = 9, x4 = 3; z = 63; dual problem: u5 = 25/4, u6 = 3/4, u7 = 35/4; w = 63

9.10 optimal solution of problem (P): x1 = 4, x2 = 2; z = 14;

optimal solution of problem (D): u3 = 2/3, u1 = 1/3, u5 = 0; w = 14

9.11(c) optimal solutions:

(1)

= 0,

x2 = 100,

x3 = 50,

x4 = 40;

z = 190;

(2)

= 50,

x2 = 0,

x3 = 100,

x4 = 40;

z = 190

10 EIGENVALUE PROBLEMS AND QUADRATIC FORMS

= 3,

λ2 = −2,

x1 = t1

= t2

;

10.1 A:

λ1

1 ,

−4

B: λ1 = 3 + i, λ2 = 3 − i, x1 = t1

x2 = t2

;

1 + i

1 − i

C: λ1 = 1, λ2 = 2, λ3 = −1,

, x2

−1

, x3

D: λ1

1, λ2 = λ3 = 2, x1

, x2

−2

;

t1, t2, t3

= R; t1, t2, t3

10.2(a) λ1 = 1.1 greatest eigenvalue with eigenvector xT = (3a/2, a), a = 0;

(b)based on a production level x1 = 3a/2 and x2 = a (a > 0) in period t, it follows

a proportionate growth by 10 per cent for period t + 1: x1 = 1.65a, x2 = 1.1a;

(c)x1 = 6, 000; x2 = 4, 000; subsequent period: x1 = 6, 600; x2 = 4, 400; two periods later: x1 = 7, 260; x2 = 4, 840

10.3 (a) A:

λ1 = 1,

λ2 = 3,

λ3 = −2,

λ4 = 5,

4/15

1/4

, x2

, x4

, x3

−2/5

;

506

Selected solutions

B :

λ1 = λ2 = 4, λ3 = −2,

x1,2 = t1

+ t2

x3 = t3

;

t1, t2

, t3, t4

−

\ { }

10.4

xTBx = xTBsx with Bs =

−

1/2

, Bs is positive definite

−1/2

10.5

(a) A: λ1,2 = 2 ± √

B: λ1,2 = (3 ±

√

)/2,

λ2,3 = 3 ± √

C: λ1 = −4,

λ2 = 2,

λ3 = 3,

D: λ1 = 1,

(b)A and D are positive definite, B and C are indefinite

10.6 (a) a1 = 3, a2 = 1, a3 R;

(b)any vector x1 = (t, t, 0)T with t R, t = 0, is an eigenvector;

(d) no

11FUNCTIONS OF SEVERAL VARIABLES

11.1(a) f (x1, x2) = √x1x2

isoquants

surface in R3

(b)domains and isoquants

(i)

(ii)

Df = {(x, y) R2| x2 + y2 ≤ 9}

Df = {(x, y) R | x = y}

Selected solutions 507

(iii)

= R

y2x(y2 −1),

11.2

(a)

2x sin2y,

(b)

) ln x;

fy = 2x2 sin y cos y;

fy = 2y x(y

(c)

fx = yx

−

+ y

ln y,

(d)

fx =

fy = x

ln x

+ xy

−

;

fy =

;

(e)

ex2 +y2 +z2 (2

4x2), (f )

fx1

= x12

+xx22 + x32

4xyex

fx2

= x12

+xx22 + x32

fz =

4xzex

;

fx3

+ x2 + x3

1, 200, 000

32, 000, 000

11.3

(a)

Cx = 120 −

Cy = 800 −

;

Cy (240) ≈ 244.5

(b)

Cx (80) = − 67.5,

Cx (120) ≈ 36.67,

Cy (160) = − 450,

11.4

(a)

fx1 x2

= fx2 x1 = 6x2x33,

fx1 x3 = fx3 x1

= 9x22x32, fx2 x3

= fx3 x2 = 18x1x2x32,

fx1 x1 = 6x1 −2

x1−2,

fx2 x2 = 6x1x33,

fx3 x3 = 18x1x22x3 − x3−2;

(b)

fxx

fyy

4x2

fxy

fyx

2xy + 2

;

= (1 − xy)3

(1 − xy)3

(c) fxx =	4xy	,	fyy = fxx ,
	(x2 − y2)2

11.5(a) grad f (1, 0) = (a, b)T,

(b)grad f (1, 0) = (2, 1)T,

(c)grad f (1, 0) = (−1/2, 0)T,

fxy	=	fyx	=	−2(x2 + y2)
	=		=	(x2 − y2)2

grad f (1, 2) = (a, b)T; grad f (1, 2) = (3, 3.6)T;

grad f (1, 2) = (−1/2, −1)T

11.6the direction of movement is −grad f (1, 1) = (−1.416, −0.909)T

11.7

(a)

dz = y cos y dx −

cos y dy;

(b)

dz = (2x + y

) dx

+ (2xy

+ cos y) dy;

(c)

dz = (2x dx + 2y dy)e

;

(d)

dz = x dx + y dy

11.8

surface: S = 28π ,

absolute error: 4.08,

relative error: 4.6 per cent

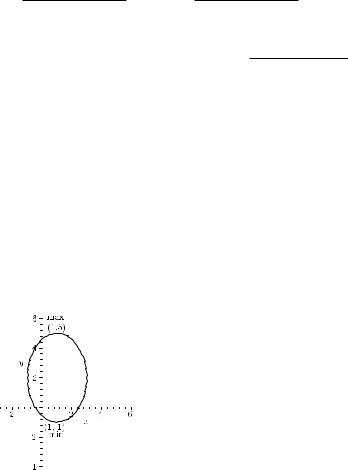
508

Selected solutions

dx1

dx2

11.9

(a)

= 2x1e

+ x1 e

;

(b)

(i)

2x1e

2 x

2t + x1 e

(ii)

2 x

2t =

t ln t ln t;

2x1e

+ x1 e

(c)

(i)

t6;

6t5,

(ii)

z = (ln t

+ t ln t) ln t

)

( t

3 √

√

∂ f

11.10

(a) = −

;

(a) = −

(a) =

∂ r1

∂ r2

∂ r3

11.11

(a)

grad C(3, 2, 1) = (8, 6, 10)

∂C

(P0) = 13.36;

∂r1

percentage rate of cost reduction: 5.52 per cent;

(b)The first ratio is better or equal

11.12	ρf ,x1	= 0.002;		ρf ,x2 = 0.00053;		εf ,x1	= 0.2;	εf ,x2 = 0.079
11.13	(a)	partial elasticities:
		εf ,x1		x1(3x12 + 2x22)	,	εf ,x2	x2(4x1x2 + 3x22)
			= 2(x13 + 2x1x22 + x2		3)		= 2(x13 + 2x1x22 + x23)
		f homogeneous of degree r = 3/2,				r > 1;

(b)f is not homogeneous

11.14

(a) y

; (b)

3x cos 3x

sin 3x ; (c) y

y(yxy − 1 + 2x2y)

−

x2−

= a x2

= − x( yxy ln x − 1 + yx2)

11.15

|J | = r;

for r = 0 : r = x

+ y , ϕ = arctan

resp. ϕ = arccos

x2 + y2

11.16local maximum at (x1, y1) = (1/2, 1/3); no local extremum at (x2, y2) = (1/7, 1/7)

11.17(a) local minimum at (x1, y1) = (0, 1/2) with z1 = −1/4;

(b)local minimum at (x1, y1) = (1, ln 43 ) with z1 = 1 − ln 43

11.18stationary point: (x0, y0) = (100, 200);

local minimum point with C(100, 200) = 824, 000

11.19local minimum point: x1 = (1, 0, 0),

x2 = (1, 1, 1), x3 = (1, −1, −1) are not local extreme points

11.20no local extremum

11.21	stationary point x = (30, 30,	15) is a local maximum point with P(30, 30, 15) =
	26, 777.5
11.22	(a) y = 10.05x − 28.25;		(b) y(18) = 152.64, y(36) = 333.5
11.23	P1: maximum; P2: minimum

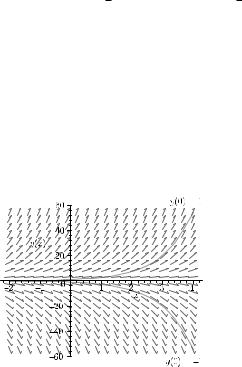
Selected solutions 509

11.24(a) local maximum at (x1, y1) = (4, 0) with z1 = 16;

(b)local minimum at (x11, x21, x31) = (−1/12, 37/12, −30) with z1 = −73/48

11.25local maximum point; values of the Lagrangian multipliers: λ1 = −13 and λ2 = −16

11.26length = breadth = 12.6 cm, height = 18.9 cm

11.27local and global maximum of distance Dmax = 84/9

√= (− 23 , − 23 √5);

=3 at point (x3, y3) = (−1, 0);1 min

local and global minimum of distance D2 min = 1 at point (x4, y4) = (1, 0)

11.28stationary point (x1, x2, x3; λ) = (25, 7.5, 15; 5); local minimum point with C(25, 7.5, 15) = 187.5

11.29136/3

11.3032/3

11.313/8

12DIFFERENTIAL EQUATIONS AND DIFFERENCE EQUATIONS

12.1(a), (c)

(b)

yP = ex

1 + ex

12.2

(a)

;

(b) y2

2 ln

12.3

ky · (x − 1) − y + 1 = 0

particular solution yP = xx2

12.4

general solution y = Cxx2 ,

12.5

y = Ct100e−t/2

12.6

The functions y1, y2, y3 form a fundamental system;

y = C1x + C2x ln x + C3 x

12.7

(a)

y = Ce

−

(b)

(1 + x);

5 cos x

5 sin x;

= e

(c)

y = C1e−x + C2ex/2 + ex ;

(d)

y = −ex cos 3x + x2 + 2.2 x + 1

y = C1 + e−x (C2 cos 2x + C3 sin 2x) +

12.8

(a)

cos x +

sin x;

(b)

y = C1ex + C2e−2x + C3xe−2x +

xex

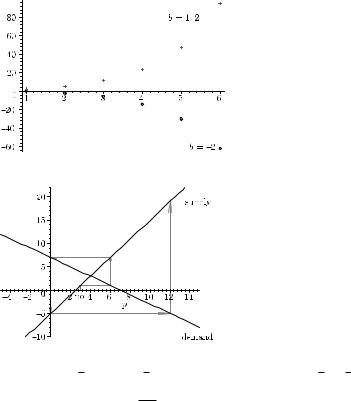
510

Selected solutions

12.9

(a)

= C1eax cos x+

C2eax sin x

(b) y1P

= 3e2x

C1eax sin x

C2eax cos x

= −

8e−x

2e2x

−

e2x

16e−x

12.10

(a)

= (1 + b)2t − b;

(b) strictly increasing for b > −1;

(c)

12.11	(a)	pt+1 = −2pt +12;		(b) pt = −(−2)t +4 with p0 = 3, p1 = 6, p2 = 0, . . .;
	(c)
		yt = 2t	2	2	;				1	2
12.12	(a)	yt = 2t	C1 cos 3 π t	+ C2 sin 3 π t	;		(b)	ytP	= 4t − (−2)t − 3 t −	3 ;
				1
	(c)	yt = C1(−1)t + C2t(−1)t + 100 · 4t						=	C1(1.5)t + C2(−0.1)t ;
12.13	(a)	yt+2	= 1.4yt+1	+ 0.15yt ;		(b)	yt	=	C1(1.5)t + C2(−0.1)t ;
	(c)	1,518.76 units
12.14	(a)		t 1			(b)	yt	= 3t y0 + 3t − t − 1
12.14	(a)	yt = 3t y0 + i=−1 (2i + 1)3t−i−1;				(b)	yt	= 3t y0 + 3t − t − 1

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1716 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.20161.12 Mб10LOGIKA_UMP_KL_STR_113_DLYa_PDF.pdf
#
03.03.201632.02 Mб17lМирошникова О.С. Microsoft Office Word.docx
#
03.03.20164.5 Mб277Manual_Maxwell_render.pdf
#
03.03.20161.44 Mб17matem_2_chast.pdf
#
03.03.2016626.51 Кб26MathCad_Metoda_Lab.pdf
#
03.03.20168.37 Mб25Mathematics of Economics and Business.pdf
#
03.03.20162.72 Mб18Mat_modeli_OSA_konspekt_lektsiy.pdf
#
03.03.20161.01 Mб21Mat_modeli_OSA_lab_rab.pdf
#
03.03.20166.75 Mб14Metodicheskie_ukazania.doc
#
03.03.20161.58 Mб11Metodicheskie_ukazania_ind.doc
#
03.03.20161.54 Mб3Metodicheskie_ukazania_prakt.doc