
ТеорПрактНаучнИссл_Устименко
.pdf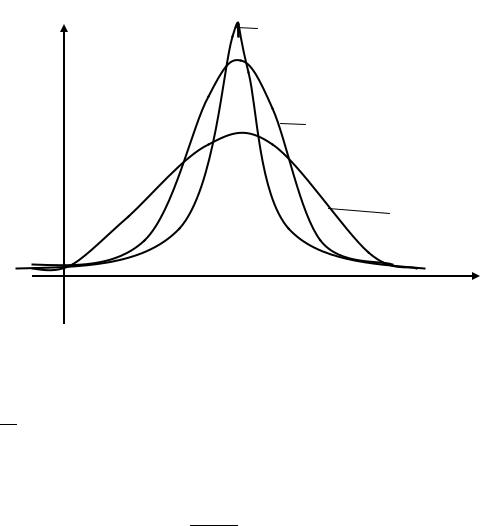
81
< 0 асимметрия называется правосторонней, в этом случае справедливо соотношение < . Для симметричного распределения справедливо = =
.
Эксцесс (коэффициент крутости). Эксцесс характеризует форму вершины кривой плотности распределения. Эксцесс указывает, насколько плотность распределения более заострена, или наоборот, полога по сравнению с плотностью нормального распределения.
E>0
f(x)
E=0
E<0
x
Рисунок 4.2 - К понятию коэффициента эксцесса
Оценка вычисляется как
= 44 − 3,
где 4- оценка центрального выборочного момента 4-го порядка рассчитывается по формуле
1
4 = − 1
− 4
=1
Эксцесс характеризует форму вершины кривой плотности распределения. Эксцесс указывает, насколько плотность распределения более заострена, или наоборот, приплюснута по сравнению с плотностью нормального распределения. Распределение считается близким к нормальному, если выборочные значения удовлетворяют условию , < 0.1. Коэффициент асимметрии и эксцесс нормально распределѐнной случайной величины равны нулю.
82
4.2.2. Оценка точности косвенных измерений
Часто интересующая нас величина непосредственно не может бить измерена, а определяется как функция других величин, которые находятся опытным путем. Например, расход воздуха в прямоугольном канале
=
где - ширина канала, м; - высота канала, м; - средняя скорость воздуха, м/с.
Для определения расхода измеряют ширину, высоту канала и среднюю скорость воздуха. При измерениях величин , и допускаются погрешности. Оценка их может быть выполнена по рассмотренной методике.
Погрешность определяемой величины зависит не только от погрешностей измеряемых, но и от вида функциональной связи между ними [4; 6].
Предположим, что величина, погрешность которой необходимо определить является произвольной функцией двух измеряемых переменных х и у:
= |
( , ) |
|
|
|
|
Подставим ряд параллельных опытов и по полученным данным найдем |
|||||
, , , . |
|
|
|
|
|
Необходимо определить Для |
-го измерения |
= + ∆ , |
= + ∆ |
, |
|
|
|
|
|
|
|
= + ∆ .
Если функция ( , ) непрерывна и во всех точках интересующего нас интервала и имеет производные, то ее, как известно, можно разложить ряд Тейлора. Выполним эту операцию и оставим в ряде только линейные члены:
+ ∆ = , + ( |
|
) |
|
∆ + ( |
|
) |
|
∆ |
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
, |
|
|||
Так как = ( , ), то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ = ( |
|
) |
|
∆ + ( |
|
) |
|
∆ |
|
|
||||||
|
|
|
|
|
|
|||||||||||
|
|
, |
|
|
|
|
|
, |
|
|
|
|
||||
Возведем правую и левую части последнего равенства в квадрат и просуммируем данные по всем измерениям:
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
(∆ )2 |
= |
(∆ )2 |
+ 2 |
|
∆ ∆ |
|
+ |
(∆ |
)2 |
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
, |
|
|
|
, |
|
|
|
|
|
|
|
|
=1 |
|
=1 |
|
, =1 |
|
|
, |
=1 |
|
Если закон распределения погрешностей симметричный, например нормальный, то ∆ , ∆ одинаково часто встречаются как со знаком "+", так и со знаком "-". Поэтому в последнем выражении
|
|
|
|
|
|
|
|
= 0 |
|
|
|
|
∆ ∆ |
|
|
|
|
||
, |
|
|
||
|
|
|
, =1 |
|
Следовательно,
|
|
|
|
83 |
|
|
|
|
|
|
2 |
|
|
|
|
(∆ )2 |
= |
(∆ )2 |
+ |
||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|
|
|
|
|
=1 |
|
, |
=1 |
|
|||
|
|
|
|
|
2
(∆ )2
, =1
Последнее равенство не нарушится, если все его члены разделить на − 1. Так как
|
|
|
|
|
∆ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
= 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
− 1 |
|
|
|
||||
|
|
=1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
2/( − 1) = 2 |
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
2/( − 1) = 2 ; |
|||||||||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
то получим |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= |
|
2 |
2 |
+ |
|
2 |
2 |
||||
|
|
|
|
|
|
|
||||||
|
|
|
, |
|
|
|
|
|
||||
|
|
|
|
|
|
, |
|
|||||
Пример. Известно, что расход воды через треугольный водослив
= 1.343 2.47,
где - уровень воды, м.
Относительная погрешность определения уровня = 1%. Определить относительную погрешность расхода.
В соответствии с полученным выше выражением
2 |
|
|
2 |
|
= |
|
2 |
, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
так как |
|
|
|
|
|
= 1,343 ∙ 2,47 (2,47−1), |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= 2 2 = |
|
1,343 ∙ 2,47 2,47 |
2/ 1,343 2,47 |
2) 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
После преобразования имеем |
|
|
|
|
|
|
|||||
|
|
|
|
2,472 |
2 |
|
|
|
|||
|
|
2 |
= |
|
|
|
|
; 2 = 2,472 2 |
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, в условиях данного примера |
= 2,47 |
= 2,47 ∙ 1% |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2,47% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2.3. Интервальные статистики
На практике в большинстве случаев параметры генеральной совокупности – математическое ожидание и дисперсия – неизвестны. Их точечные оценки – выборочное среднее и выборочная дисперсия – являются случай-

84
ными величинами, причем при условии < 25 эти оценки считаются не надежными. Поэтому часто используют т.н. интервальные статистики.
Двухсторонний доверительный интервал
Точечные оценки имеют тот недостаток, что по ним нельзя судить о точности полученных оценок. Поэтому возникает задача определения на основании выборочных значений такого интервала, который покрывал бы неизвестной значение параметра с заданной вероятностью.
В отличие от точечной оценки, интервальная оценка позволяет получить вероятностную характеристику точности оцениваемого параметра.
Выборочные параметры являются случайными величинами, их отклонения от генеральных (т.е. погрешности их определения) также будут случайными. Оценка этих отклонений носит вероятностный характер – можно лишь указать вероятность той или иной погрешности. Для этого в математической статистике пользуются доверительными интервалами и доверительными вероятностями.
Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.
Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.
Оценивание с помощью доверительного интервала – способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Рисунок 4.3 - Двухсторонний доверительный интервал
На числовой оси в обе стороны от оценки строится интервал с границами , в который оцениваемый параметр попадет с заранее выбранной вероятностью
− < = 1 − |
(4.1.) |
где - уровень значимости, обычно, = 0.1,0.05 |
или 0.01 . Часто выража- |
ется в процентах. Уровень значимости связан с доверительной вероятностью
(надежностью) формулой
= 1 − |
(4.2) |
Интервал − , + называется двухсторонним доверительным интерва-
лом, который покрывает параметр с надежностью (1 − ). Чем меньше
85
значение интервала для выбранной вероятности , тем точнее оценка параметра . Варианты вычисления доверительных интервалов для оценки математического ожидания и дисперсии рассмотрены в разделе 4.2.3.
Функции распределения
Вычисление доверительных интервалов, проверка статистических гипотез (раздел 4.5) и построение модели объекта с помощью факторного эксперимента (раздел 4.3) опирается на знание различных законов распределения вероятности. Более подробная информация о вероятностных законах распределения приведена в Приложении 1, ниже будут приведены способы применения основных законов распределения для построения доверительных интервалов при оценивании основных статистик.
Нормальное распределение. В инженерной практике при обработке экспериментальных данных обычно предполагается нормальный закон распределения случайных погрешностей измерений. Нормальный закон всегда проявляется там, где суммарная погрешность измерений есть результат совместного действия множества факторов, каждый из которых дает свой незначительный вклад в погрешность. При этом закон распределения каждого фактора в отдельности не имеет значения.
При обработке результатов эксперимента широко используется «правило 3 », или правило «трех стандартов». Суть его в том, что для нормального распределения справедливо соотношение
− < 3 = 2Φ 3 = 0.9973
Следовательно, можно считать, что практически все измеренные значения будут лежать в интервале − 3 < < − 3 . Так как обычно реально известны только выборочное среднее и выборочное среднеквадратическое отклонение , то можно считать, что все измеренные значения должны лежать в интервале − 3S < < − 3S и в этом случае следует говорить о «правиле 3 ». С его помощью обычно оценивают возможный разброс значений параметров технической системы.
Следует заметить, что если результат измерения отличается от выборочного среднего на величину, большую 3 , то необходимо более тщательно повторить измерения. Возможно, что полученный результат измерения не является промахом, а является выражением необычного поведения устройства и не укладывается в рамки существующих представлений о нем (например, имеет место явление резонанса).
При обработке случайных данных, имеющих нормальное распределение, возникает несколько новых видов распределений, а именно: 2 - распределение, распределение Стьюдента и − распределение, которые широко используются в экспериментальных исследованиях.
86
2-распределение. При увеличении числа степеней свободы N данное распределение медленно приближается к нормальному распределению. Область использования 2 - распределения - вычисление доверительного интервала для дисперсии, проверка гипотезы о значении дисперсии и законах распределения.
Распределение Стьюдента (t-распределение). При увеличении числа степеней свободы N данное распределение быстро приближается к нормальному распределению. Область использования t- распределения - вычисление доверительного интервала для математического ожидания, проверка гипотезы о значении математического ожидания.
Распределение Фишера (F-распределение) или распределение отноше-
ния дисперсий широко используется при решении многих технических задач, в частности для выявления роли факторов, определяющих свойства того или иного объекта, для оценки адекватности статистической модели.
Более подробная информация об этих и некоторых других вероятностных распределениях приведена в Приложении 1.
4.2.4. Расчет доверительных интервалов
Доверительные интервалы дают больше информации о параметре, чем точечная оценка, так как показывают совокупность допустимых значений.
Понятие доверительного интервала тесно связано с понятием точности прибора. Класс точности прибора – это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора. В измерительной технике в большинстве отраслей промышленности под предельной погрешностью понимается величина, равная двум среднеквадратическим отклонениям Например, если класс точности прибора = ( – )/ =
0.01 (1%) а этот прибор – манометр с максимальным значением давления по шкале 100кгс/см2, то абсолютная погрешность этого прибора
= ( − ) = 100 0.01 = 1ат = 2 х,
следовательно, х =0,5 ат .
Пусть имеется выборка объемом значений случайной величины. Оцен-
|
|
|
|
|
кой |
|
является среднее выборки: = |
=1 |
|
|
|
|||
|
|
|
||
|
|
|
|
Для построения доверительного интервала необходимо знать распределение этой оценки. Для выборок из генеральной совокупности, распределенной
нормально, |
доказано, что x также имеет нормальное распределение с матема- |
||||||||||||
тическим ожиданием |
|
и среднеквадратическим отклонением (стандартной |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ошибкой) |
|
= |
|
. Тогда |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
√ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
− |
|
≤ |
= = 2Φ( |
) |
(4.3) |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||

87
Задавшись доверительной вероятностью, определим по таблице значение функции Лапласа = / . Тогда доверительный интервал для математического ожидания будет иметь вид
− |
|
≤ |
|
≤ + |
или |
|
|
|
|
|
− /√ ≤ ≤ + /√
Из оценки видно, что уменьшение доверительного интервала обратно пропорционально квадратному корню из числа наблюдений. Следовательно, если надо уменьшить возможную ошибку в два раза надо увеличить число наблюдений в 4 раза.
Если закон распределения оценки не известен, то в математической статистике применяют обычно два метода:
1)приближенный – при более 50 заменяют неизвестные параметры их оценками;
2)от случайной величины переходят к другой случайной величине, закон распределения которой не зависит от оцениваемого параметра , а зависит только от объема выборки и от вида распределения величины Х. Такого рода величины наиболее подробно изучены для нормального закона. В качестве доверительных границ берут симметричные квантили
1− /2 ≤ ≤ 1+ /2
Если выразить через ,
|
≤ ≤ |
/2 |
1−/2 |
На практике, как правило, число измерений конечно и не превышает
10…30. При малом числе измерений фактическая дисперсия 2 неизвестна, по-
этому для построения доверительного интервала математического ожидания
используют выборочную дисперсию 2 и приведенную случайную величину:
= −√
– случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы( – распределение или распределение Стьюдента). При больших значениях распределение Стьюдента приближается к стандартному нормальному распределению. И, по аналогии, получаем по-
строение доверительного интервала |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
− |
, |
|
≤ ≤ + |
, |
|||||
|
|
|
|
|
|
|
|||
|
|
|
√ |
||||||
|
|
√ |
|
||||||
4.2.5. Определение необходимого количества опытов
Необходимое количество измерений (образцов, проб и т.д.) n можно определить заранее в том случае, когда известно действительное значение средне-

88
квадратического отклонения, а экспериментальные данные подчиняются нормальному закону распределения.
Действительно, при этих допущениях число измерений можно определить из системы неравенств:
− /√ ≤ ≤ + /√
Анализируя формулу доверительного интервала, можно заметить, что:
а) увеличение объема выборки приводит к уменьшению длины доверительного интервала;
б) увеличение доверительной вероятности приводит к увеличению дли-
ны доверительного интервала, т.е. к уменьшению точности = |
|
|
; |
|||
|
|
|||||
|
|
|
√ |
|||
в) если задать точность и доверительную вероятность , то из соотноше- |
||||||
ния = |
|
|
можно найти минимальный объем выборки, который обеспечи- |
|||
|
||||||
|
|
|||||
√
вает заданную точность.
Однако, в эксперименте значение оценивают, исходя из конечного числа измерений, количество которых обычно не превышает 5-10. Поэтому точность оценивания невелика. Это вносит дополнительную неопределенность в окончательный результат. Чтобы ее учесть, необходимо расширить границы доверительного интервала, заданного для точно известной величины . Понятно, что меньшему количеству отдельных измерений должен соответствовать
более широкий доверительный интервал. Поэтому |
на практике используется |
||||
формула |
|
|
|
|
|
− |
|
≤ ≤ + |
, |
||
α, |
|
|
α, |
|
|
Где α, - квантиль распределения Стьюдента, |
определяемый уровнем |
||||
значимости α и количеством степеней свободы = − 1.
4.2.6. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии
Пусть каким-либо образом известна дисперсия 2 генеральной совокупности. Тогда доверительный интервал для математического ожидания определяется как
|
|
− ε |
≤ ≤ + ε |
||||
причем |
= |
, где |
= |
|
|
- стандартная ошибка, - квантиль |
|
|
|
|
|||||
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
||
нормального распределения порядка. Квантиль есть решение уравнения |
|||||||
|
|
|
|
|
|
|
|
|
|
2Φ |
|
= = 1 − |
|||
|
|
|
|
|
|
|
|
где Φ - функция Лапласа. Квантиль может быть определен из таблиц функции Лапласа. Таким образом, можно говорить, что математическое ожи-

|
|
89 |
дание |
|
с вероятностью 1 − 100% лежит в доверительном интервале |
|
|
|
(118). |
|
|
Из анализа вышеизложенного следует, что:
Чем больше объем выборки , тем выше точность интервального оценивания, так как уменьшается значение интервала ε ;
Чем больше значение дисперсии , тем ниже точность интервального оценивания, так как увеличивается значение интервала ε ;
Чем больше значение надежности оценки 1 − , тем ниже точность интервального оценивания, так как увеличивается квантиль и, соответственно,
увеличивается значение интервала ε .
Заметим, что правило «трех стандартов» для данного случая представляет собой доверительную оценку истинного значения измеряемой величины
− < 3
√
с надежностью 2Φ 3 ≈ 0.9973 независимо от количества из-
мерений.
4.2.7. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии
В этом случае доверительный интервал для математического ожидания
определяется в соответствии с ( ), но значение интервала вычисляется как
= 1− , √
где - выборочное среднеквадратическое отклонение, 1− - квантиль распределения Стьюдента порядка 1 − и с числом степеней свободы − 1.
При объемах выборки > 100 вместо квантиля 1− можно использовать квантиль нормального распределения , который не зависит от значения объема выборки .
Заметим, что правило «трех стандартов» для данного случая представляет
собой доверительную оценку истинного значения измеряемой величины |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
− < |
3 |
|
с надежностью1 − , зависящей от количества измерений. За- |
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
|
|
√ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
висимость надежности от количества измерений N представлена в таблице 5. |
|||||||||
|
|
|
|
|
|
|
Таблица 4.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
0.960 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
0.985 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
0.993 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
0.995 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
150 |
|
0.997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.9973 |
|
|
|
|
|
|
|
|
|
|
|
90
4.2.8. Доверительный интервал для дисперсии нормальной генеральной совокупности
Доверительный интервал для дисперсии нормальной генеральной совокупности вычисляется как
( − 1) 2 |
|
( − 1) 2 |
||
|
|
|
< 2 < |
|
|
2 |
|
2 |
|
|
|
|
||
1−2 |
|
2 |
||
где |
2 |
- |
выборочная дисперсия, |
2 |
|
, |
2 |
- квантили порядка соответст- |
|||||
|
|
|
|||||||||||
|
|
|
|
1− |
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
2 |
|
|
||||
венно 1 − |
|
и |
|
2-распределения с − 1 степенями свободы. |
|||||||||
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
4.3 Проверка статистических гипотез 4.3.1. Постановка задачи
Проверка статистических гипотез является одной из основных задач математической статистики. Суть этой задачи состоит в том, что на основании выборочных данных должно быть принято или отвергнуто некоторое предположение (статистическая гипотеза) относительно генеральной совокупности.
Процедура сопоставления гипотезы с выборочными данными называется
проверкой гипотез.
Задача статистической проверки ставится в следующем виде: относительно некоторой генеральной совокупности высказывается та или иная гипотеза Н. Из генеральной совокупности извлекается выборка. Требуется указать правило, при помощи которого можно было бы по выборке решить вопрос, следует ли принять гипотезу Н, либо отклонить ее. Например, эффективнее ли лекарство, испытанное на определенном числе людей, по сравнению с другими способами лечения? Аналогично можно поставить вопрос о новых правилах приема в вуз, методах обучения, преимуществах новой разрабатываемой техники т.п.
Выдвигаемая гипотеза может быть правильной или неправильной, поэтому возникает задача ее проверки.
Итак, под статистической гипотезой будем понимать всякое высказывание о генеральной совокупности, проверяемое по выборке.
Статистические гипотезы делятся на параметрические (гипотезы о параметрах распределения) и непараметрические (о виде неизвестного распределения). Например:
Математическое ожидание |
равно конкретному числу (параметри- |
||
|
|
|
0 |
ческая гипотеза) |
|
|
|
Дисперсия 2 |
равна конкретному числу 2 |
(параметрическая); |
|
|
|
0 |
|
Генеральная совокупность распределена по нормальному закону (непараметрическая);
