
Nazarova_Met-ka_po_DM_2006
.pdf
29
4.6 Фиктивные аргументы ФАЛ
Две ФАЛ f1(x1, x2, … , xn) и f2(x1, x2, … , xn) называются равными, если они принимают одинаковые значения на всех возможных наборах аргументов.
ФАЛ называется существенно зависящей от аргумента xi, если имеет место неравенство:
f1(x1, x2, … , xi-1, 0, xi+1, … , xn) ≠ f2(x1, x2, … , xi-1, 1, xi+1, …, xn).
В противном случае говорят, что функция несущественно зависит от xi, и xi является ее фиктивным аргументом.
ФАЛ не изменится, если к ее аргументам приписать или вычеркнуть любое количество фиктивных аргументов.
4.6.1Алгоритм нахождения фиктивных аргументов Для нахождения фиктивных аргументов необходимо задать ФАЛ таблично:
1)Разбить множество наборов аргументов ФАЛ на 2 подмножества: 1-
еподмножество, на котором функция принимает значение 0, и 2-е подмножество, где функция принимает значение 1, соответственно множества Т0 и Т1.
2)Для проверки фиктивности аргумента xi вычеркиваем столбец, который ему соответствует, и проверяем, не появились ли в двух подмножествах одинаковые наборы. Если такие наборы не появились, то xi является фиктивным.
Например: |
|
|
|
|
Имеет ли функция |
F ( x , y , z ) = x ≡ y ↓ z y & ( |
|
) |
фиктивные |
z → x |
||||
аргументы? |
|
|
|
|
Решение |
|
|
|
|
30
x |
y |
z |
F(x, y,z) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
|
Множество Т0: |
|
|||
x |
y |
z |
F(x, y,z) |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
|
Множество Т1: |
|
|||
x |
y |
z |
F(x, y,z) |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
Если вычеркнуть x во множестве Т0 и Т1, то появятся одинаковые наборы. Следовательно, х не является фиктивным аргументом функции F(x,y,z). Аналогично для аргументов y и z. В результате, функция F(x,y,z) не имеет фиктивных аргументов.
4.7 |
Законы булевой алгебры |
|
|
|
|
Коммутативность |
Свойства констант |
|
x 1 |
x 2 = x 2 x 1 |
x 1 =1 |
x 1 |
& x 2 = x 2 & x 1 |
x 0 = x |
Ассоциативность |
x &1 = x |
|
x1 & (x2 & x3 ) = (x1 & x2 ) & x3 |
x & 0 = 0 |
|
x1 (x2 x3 ) = (x1 x2 ) x3 |
Законы де Моргана |
|
Дистрибутивность |
|
|

31
x1 & (x2 x3 ) = x1 & x2 x1 & x3
x1 (x2 & x3 ) = (x1 x2 ) & (x1 x3 )
Идемпотентность
x x = x
x & x = x
Закон отрицания отрицания
x = x
Закон исключающего третьего
x x =1
Закон противоречия x & x = 0
x1 & x2 = x1 x2
x1 x2 = x1 & x2
Законы поглощения x1 x1 x2 = x1
x1 (x1 x2 ) = x1
Правила склеивания
x1 x2 x1 x2 = x1
(x1 x2 ) & (x1 x2 ) = x1
Обобщенное склеивание
x1 x3 x2 x3 x1 x2 = x1 x3 x2 x3
Правило вычеркивания
x1 x1 x2 = x1 x2
Свойства ↓, , , →
Свойства импликации x → x =1
x → |
|
= |
|
|
|
|
x1 → x2 |
= |
|
x2 |
→ |
x1 |
||||
x |
x |
|||||||||||||||
x →1 =1 |
x1 → x2 |
→ x1 = x1 |
||||||||||||||
|
|
|
x1 x2 = |
|
|
→ x2 |
||||||||||
x → 0 = |
|
|
|
x1 |
||||||||||||
x |
||||||||||||||||
0 → x =1 |
|
|
|
|
||||||||||||
x1 & x2 = x1 → |
|
|
|
|||||||||||||
x2 |
||||||||||||||||
1 → x = x |
|
|
|
|
|
|
|
|
|
|
||||||
x1 → x2 ≠ x2 → x1
x1 → (x2 → x3 ) ≠ (x1 → x2 ) → x3
Свойства
x1 x2 = x2 x1
x1 (x2 x3 ) = (x1 x2 ) x3 x x = 0
x 0 = x x 1 = x x x =1
x1 x2 = x1 x2 x1 x2
Свойства функций Шеффера и стрелки Пирса
x1 | x2 = x2 | x1 x1 ↓ x2 = x2 ↓ x1
(x1 | x2 ) | x3 ≠ x1 | (x2 | x3 )
(x1 ↓ x2 ) ↓ x3 ≠ x1 ↓ (x2 ↓ x3 )
x | x = |
x |
x ↓ x = |
|
|
|
||||||||
x |
|||||||||||||
x |1 = |
|
|
x ↓ 0 = |
|
|
|
|
||||||
x |
|
x |
|
||||||||||
x | |
|
=1 |
x ↓ |
|
= 0 |
||||||||
x |
|||||||||||||
x |
|||||||||||||
x | 0 =1 |
x ↓1 = 0 |
||||||||||||
Функции ↓ и связаны соотношениями аналогичными формулам де Моргана
x1 | x2 = x1 ↓ x2
x1 ↓ x2 = x1 | x2
4.8 Выражение одних элементарных функций через другие

32
x1 → x2 = x1 x2
x1 x2 = x1 ≡ x2 = x1 x2 x1 x2 = ( x1 x2 ) ( x1 x2 ) x1 ≡ x2 = x1 x2 x1 x2 = x1 x2 = ( x1 x2 ) ( x1 x2 )
x1 x2 = x1 x2 x1 x2 = x1 x2
x1 | x2 = x1 x2 = x1 x2 x1 ↓ x2 = x1 x2 = x1 x2
4.9 Аналитическая запись ФАЛ
Рассмотрим методы перехода от табличного способа задания функций к аналитическому методу (в виде формул).
4.9.1 Дизъюнктивная нормальная форма (ДНФ)
Конъюнкция называется элементарной, если в ней каждая переменная встречается не более одного раза.
Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).
Например:
Используя законы алгебры логики преобразовать пошагово функцию F(x,y,z) в ДНФ.Для полученного результата составить таблицу истинности.
Решение
Выполним преобразования по действиям:
1.z → x = z x
2.z x = x z
3.y ↓ z = y z = y z
4.x z & y = x y z
5.x ≡ y z = x y z x y z = x y z x y x z
6. (x y z x y x z) x y z = (x y z x y x z) x y z (x y z x y x z) x y z =
(x y z x y x z) (x y z) (x y z x y x z) x y z =
(x y z x x y x x z x y y x y z x y z x z z) (x y z) (x y) (x z) x y z = (x y z x y z x y z) (x y z) (x y) (x z) x y z =
(x y z x y z x y z) (x y z) (x y) (x x y z z x y z) =
(x y z x y z x y z) (x y z) (x y) 0 = x y z x y z x y z .
Составим таблицу истинности для полученного результата:
33
Таблица 5. Таблица истинности для полученного результата
x |
y |
z |
x |
y |
z |
x y z |
x y z |
x y z |
F(x, y,z) |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Сравнив столбцы, соответствующие функциям в таблицах №4 и №5, необходимо получить одинаковые значения функции.
И так как в построенных таблицах соответствующие столбцы равны, можно сделать вывод, что перевод в ДНФ верен.
4.9.2 Дизъюнктивная совершенная нормальная форма (ДСНФ)
Любая таблично заданная ФАЛ f(x1, x2, …, xn) (кроме тождественного нуля) может быть представлена в следующем аналитическом виде:
f ( x1 ,x2 ,...,xn ) = x1α1 & xα2 2 & ...& xαn n
T1
Представление ФАЛ в таком виде называется дизъюнктивной совершенной нормальной формой этой функции (ДСНФ).
4.9.3Алгоритм перехода от табличного задания функции к ДСНФ
1.Выбрать в таблице все наборы аргументов, на которых функция обращается в единицу.
2.Выписать конъюнкции, соответствующие этим наборам аргументов. При
этом, если аргумент xi входит в данный набор как 1, он вписывается без изменения в конъюнкцию, соответствующую данному набору. Если xi входит в данный набор как 0, то в конъюнкцию вписывается его отрицание.
4.9.4Конъюнктивная совершенная нормальная форма (КСНФ)
Любая таблично заданная ФАЛ f(x1, x2, …, xn) (кроме тождественной единицы) может быть представлена в следующем аналитическом виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( x ,x |
|
,...,x |
|
) = |
|
α |
x |
α |
... x |
α |
|
||||
|
|
x |
1 |
2 |
|
n |
|||||||||
1 |
2 |
|
n |
|
& |
1 |
|
|
2 |
|
|
n |
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

34
Представление ФАЛ в таком виде называется конъюнктивной совершенной нормальной формой этой функции (КСНФ).
4.9.5Алгоритм построения конъюнктивной совершенной нормальной формы
1.Выбрать в таблице все наборы аргументов, на которых функция обращается в
0.
2.Выписать дизъюнкции, соответствующие этим наборам аргументов. При этом,
если аргумент xi входит в данный набор как 0, он вписывается без изменения в дизъюнкцию, соответствующую данному набору. Если xi входит в данный набор как 1, то в дизъюнкцию вписывается его отрицание.
Например:
Построить ДСНФ и КСНФ для функции F(x,y,z).
F ( x , y , z ) = x ≡ y ↓ z y & ( z → x )
Решение
Для нахождения ДСНФ выбираем из таблицы №4 только те строки, в которых стоят наборы значений аргументов, обращающие функцию в единицу. Это вторая, третья и пятая строки. Выпишем конъюнкции, соответствующие выбранным строкам:
x y z, x y z , x y z .
Соединяя эти конъюнкции знаками дизъюнкции, получаем:
F( x, y, z) = x y z x y z x y z .
Для нахождения КСНФ выбираем из таблицы №4 только те строки, в которых стоят наборы значений аргументов, обращающие функцию в ноль. Выпишем соответствующие дизъюнкции и соединим их знаками конъюнкции.
Получим:
F( x, y, z ) =( x y z )( x y z )( x y z )( x y z )( x y z ) .
4.10 Полные системы ФАЛ
Система ФАЛ {f1, f2,…, fn} называется полной в некотором классе функций, если любая функция из этого класса может быть представлена суперпозицией этих функций.
Система ФАЛ, являющаяся полной в некотором классе функций, называется базисом.
35
Минимальным базисом называется такой базис, для которого удаление хотя бы одной из функций fi, которые его образуют, превращает эту систему функций в неполную.
Любая функция может быть представлена с помощью элементарных функций {¬, &, }. Эта система ФАЛ образует универсальный базис.
Наиболее популярными в алгебре логики являются базисы{ ,¬},{&,¬}, {↓},{|}, которые являются минимальными.
Например:
Представить функцию F ( x , y , z ) = x ≡ y ↓ z y & ( z → x ) в базисах { , ¬}, {|}. Для проверки результата составить таблицу истинности.
Решение
Для перевода в базис { , ¬} применим закон де Моргана к ДСНФ функции.
F (x, y, z) = x y z x y z x y z = x y z x y z x y z
Для перевода функции в базис {|} применим следующие соотношения к ДСНФ функции:
x y = x | y x y = x | y x = x | x
Обозначим F( x, y,z ) = x y z x y z x y z
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
B |
|
|
C |
|||
Выполним перевод в базис {|} по действиям. |
||||||||||||||||||||||||||||
1 |
|
|
|
|
= ( x y ) z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A |
( x | y ) z = x | y | z = [( x | ( y | y ))| ( x | ( y | y ))| ( z | z )] | |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[( x | ( y | y )) | ( x | ( y | y )) | ( z | z )] |
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
= ( x y ) z = |
|
|
|
|
| z = [(( x | x )| ( y | y ))| (( x | x )| ( y | y ))| z ] | |
||||||||||||||||||||
|
B |
x | y |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[(( x | x ) | ( y | y )) | (( x | x ) | ( y | y )) | z ] |
||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
= x y z = |
|
|
|
|
|
| z = [(( x | x ) | y ) | (( x | x )| y )| ( z | z )] | |
||||||||||||||||||
C |
x | y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[(( x | x ) | y )| (( x | x ) | y ) | ( z | z )] |
||||||||||||
4 |
|
F( x, y,z ) = ( |
|
|
|
) |
|
= ( A | B ) |
|
= |
|
| C = [( A | B ) | ( A | B )] | C |
||||||||||||||||
|
A |
B |
C |
C |
A | B |
|||||||||||||||||||||||
Проверим преобразования с использованием таблицы истинности:

36
A = [( x | ( y | y )) | ( x | ( y | y )) | ( z | z )] | [( x | ( y | y ))| ( x | ( y | y )) | ( z | z )]
2 |
1 |
|
3 |
|
5 |
4 |
6 |
|
|
|
|
|
|
|
||
Таблица 6. Таблица истинности для выражения |
|
: |
||||||||||||||
A |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
№ |
x |
Y |
z |
y | |
x | (y | |
3 |
z | |
5 |
6 |
|
x y z |
|||
|
|
|
|
|
|
|
y |
y) |
|
|
z |
|
|
|
|
|
|
|
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
|
0 |
|
|
|
1 |
0 |
|
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
|
|
|
2 |
0 |
|
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
|
|
|
3 |
0 |
|
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
|
|
|
4 |
1 |
|
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
|
|
|
5 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
0 |
|
|
|
6 |
1 |
|
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
0 |
|
|
|
7 |
1 |
|
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
|
Аналогично, проверяем B и C .
Для проверки, построим таблицу истинности для полученной формы функции F(x, y, z).
F( x, y,z ) = ( A B ) C = ( A | B ) C = A | B | C = [( A | B ) | ( A | B )] | C
Таблица 7. Таблица истинности для F(x, y, z)
№ |
x |
y |
z |
|
|
|
|
|
|
|
|
|
A |
B |
C |
A | |
|
|
|
|
A | B |
| C |
|
A |
|
|
B |
|
|
C |
A | B |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
|
1 |
1 |
1 |
0 |
1 |
|
0 |
|
|||||
1 |
0 |
0 |
1 |
0 |
|
1 |
|
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
|
|||||
2 |
0 |
1 |
0 |
0 |
|
0 |
|
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
|
|||||
3 |
0 |
1 |
1 |
0 |
|
0 |
|
0 |
|
1 |
1 |
1 |
0 |
1 |
|
0 |
|
|||||
4 |
1 |
0 |
0 |
1 |
|
0 |
|
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
|
|||||
5 |
1 |
0 |
1 |
0 |
|
0 |
|
0 |
|
1 |
1 |
1 |
0 |
1 |
|
0 |
|
|||||
6 |
1 |
1 |
0 |
0 |
|
0 |
|
0 |
|
1 |
1 |
1 |
0 |
1 |
|
0 |
|
|||||
7 |
1 |
1 |
1 |
0 |
|
0 |
|
0 |
|
1 |
1 |
1 |
0 |
1 |
|
0 |
|
|||||
Cтолбцы, соответствующие функции F(x, y, z) в таблицах №7 и №4 равны, следовательно, преобразования выполнены правильно.
4.11 Контрольные вопросы
1.Определение двоичного набора.
2.Определение булевой функции или функции алгебры логики (ФАЛ).
37
3.Область определения и область значений ФАЛ.
4.Фиктивные аргументы ФАЛ.
5.ФАЛ от одной переменной.
6.Элементарные ФАЛ от двух переменных.
7.Основные законы алгебры логики.
8.Полные системы функций, минимальный базис.
9.Аналитическое описание ФАЛ: дизъюнктивная и конъюнктивная нормальные формы.
38
5 МЕТОДЫ МИНИМИЗАЦИИ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ.
5.1 Основные определения
Буква − переменная или ее отрицание.
Элементарная конъюнкция – конъюнкция, в которой каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма(ДНФ) – дизъюнкция элементарных конъюнкций.
Ранг элементарной конъюнкции – количество переменных, которые ее образуют.
Дизъюнктивная совершенная нормальная форма (ДСНФ) – ДНФ,
состоящая из конъюнкций ранга n, где n – количество переменных. Длина ДНФ ( L ) – число конъюнкций, которые ее составляют.
Кратчайшая ДНФ – ДНФ, имеющая наименьшую длину L по сравнению с другими ДНФ, эквивалентными данной функции.
Минимальная ДНФ – ДНФ, имеющая наименьший суммарный ранг по сравнению с другими ДНФ, эквивалентными данной функции.
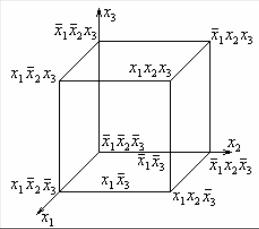
5.2 Минимизация ФАЛ на кубе
Рассмотрим проблему минимизации для геометрического способа задания ФАЛ на кубе.
Сопоставим различным геометрическим элементам куба (вершинам, ребрам, граням и кубу) конъюнкции различных рангов. Сумма размерности геометрического эквивалента и ранга конъюнкции, ему соответствующей, равна числу аргументов ФАЛ.
Каждый геометрический элемент меньшей размерности покрывается геометрическими элементами большей размерности.
Каждая конъюнкция большего ранга покрывается всеми конъюнкциями меньшего ранга.
Геометрические эквиваленты называют интервалами.
