Информатика_всем

for j:=1 to M do

if A[i,j]>Max then Max:=A[i,j];

for i:=1 to N do for j:=1 to M do

A[i,j]:=A[i,j]/Max;

Транспонирование

Транспонирование – процесс замены строк в матрице столбцами. Т.е., например, если исходная матрица имеет вид:

Алгоритм обмена таков: for i:=1 to N do

for j:=1 to i do begin

buf := A[i,j]; A[i,j] := A[j,i]; A[j,i] := buf;

end;

Матричное умножение

Матричное умножение важная операция, при перемножении матриц имеет значение порядок следования, т.е. Ошибка! Объект не может быть создан из кодов полей редактирования.. Перемножение матриц происходит по принципу «строка на столбец», для этого необходимо, чтобы число столбцов в первой матрице равнялось числу строк во второй:

На языке Pascal алгоритм таков: for i:=1 to Na do

for j:=1 to Mb do begin

C[i,j]:=0;

for k:=1 to MaNb do C[i,j]:=C[i,j]+A[i,k]*B[k,j];

end;

Определитель матрицы

Один из наиболее простых для реализации методов расчета определителя матрицы основан на методе исключения Гаусса. Суть его сводится к тому, что исходная матрица преобразуется к диагональному виду. Т.е., например, к виду верхней треугольной, что означает равенство нулю всех элементов под главной диагональю. Для треугольной матрицы определитель считается очень просто: он равен произведению элементов стоящих на главной диагонали.

Метод исключения Гаусса основывается на факте что любые строки или столбцы в матрице можно складывать между собой, умножая на произвольный коэффициент.

Сначала домножаем первую строку на соответствующий коэффициент для каждой строчки ниже, вычитая полученные значения из текущей. Таким образом, обнуляем все элементы под элементом a11 . Далее домножаем вторую

строку на нужные коэффициенты для каждой строчки ниже второй для последующего ее вычитания. Этим добиваемся чтобы под элементом a22

стояли все нули. Так продолжаем до тех пор, пока все элементы под главной диагональю не будут обнулены.

и так далее, пока не будет получена верхняя треугольная матрица. Представленный алгоритм подразумевает, что на главной диагонали

элементы не равны нулю. Если же мы будем составлять алгоритм для более общего случая, то это исключение придется учитывать. Делается это очень просто. Нужно попытаться переставить строку с нулем на главной диагонали с любой строкой ниже, которая, встав на место текущей, не будет обладать данным недостатком. Следует напомнить, что перестановка строк эквивалентна умножению определителя на –1.

Итак, алгоритм расчета определителя, предполагающий отсутствие нулей на главной диагонали следующий:

for k:=1 to N-1 do for i:=k+1 to N do

begin buf:=A[i,k]; for j:=k to N do

A[i,j]:=A[i,j]-A[k,j]*buf/A[k,k]; end;

det:=1;

for k:=1 to N do det:=det*A[k,k];

7.ПОДПРОГРАММЫ

7.1Иерархия. Черный ящик. Подпрограмма

Сознание человека устроено таким образом, что восприятие окружающей действительности происходит по принципам подобия. Это значит, например, что научившись некоторым базовым операциям, мы впоследствии опираемся на полученный опыт, пытаясь применить его к новой ситуации. Человек воспринимает мир иерархически. Отчасти это связано с особенностью способности мыслить методами формальной логики используя язык, с помощью которого человек общается с другими людьми.

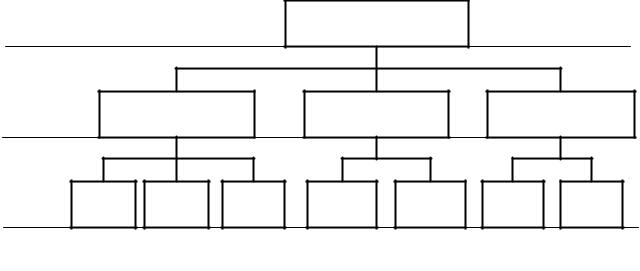
Законы иерархии предполагают наличие в воспринимаемом объекте различных уровней с четкими законами подчинения. Именно по законам иерархии наиболее часто строятся схемы управления людскими коллективами. Т.е. такие схемы, которые предполагают наличие начальника сверху, нескольких начальников чуть ниже, подчиняющихся главному. У каждого из них, соответственно, есть свои подчиненные и т.д. (Рисунок 7.1). Одна из самых жестких систем такого типа – это система военной субординации. Важным свойством систем подобных изображенной на (Рисунок 7.1) является самоподобие. Самоподобие позволяет для задания экземпляра системы описать лишь порядок взаимодействия между родительским и подчиненным модулем, а далее эти свойства распространить на все урони иерархии.

Программирование, как мы помним, тоже является средством управления. Только здесь в качестве подчиненных выступают не люди, а информация. Иерархия при программировании строится по схеме аналогичной Рисунок 7.1. Следует обратить внимание на отсутствие связей между блоками на одном иерархическом уровне.

Рисунок 7.1 Иерархическая организация

Рисунок 7.3 Графическое обозначение подпрограммы

Подпрограмма описывается один раз и может быть затем неоднократно вызвана в разделе операторов программы или другой подпрограммы. Вызов подпрограммы (т.е. ее реальное использование) приводит к выполнению входящих в нее операторов. После их выполнения работа программы продолжается с оператора, который следует непосредственно за вызовом подпрограммы, в вызывающем блоке.

При вызове подпрограмма может получать исходные данные от вызывающего блока и, при необходимости, возвращать ему результат работы.

В Pascal подпрограммы бывают двух видов: процедуры и функции. Разница между ними достаточно условна1. Суть этой разницы сводится к различию методов работы с ними.

Использование подпрограмм позволяет вывести процесс программирования на качественно иной уровень. Т.к. подпрограммы, по сути, являются независимыми блоками, то их разработку можно вести последовательно, шаг за шагом. Более того, различные участки кода, объединенные в общие библиотеки можно поручать разным программистам. Это позволяет более четко выделить сферы ответственности и разбить процесс программирования во времени и по степени сложности. Кроме того, выделив в подпрограммы многократно повторяющиеся действия, можно получить существенное сокращение программного текста, чем достигается более высокая наглядность и меньшая загруженность памяти ЭВМ.

Как процедуры, так и функции, являясь алгоритмами написанными пользователем языка программирования Pascal, и имеющими уникальное имя на своем уровне иерархии в программе, на блок-схемах изображаются блоком предопределенного процесса, имеющего вид Рисунок 7.3.

7.2 Подпрограммы в языке Pascal

Использование подпрограмм вносит иерархическую зависимость в алгоритм решения задачи, т.е. одна часть программы подчиняется другой, также соблюдается принцип вложенности, то есть любой блок может содержать внутренние блоки. Поэтому рекомендуется придерживаться следующей последовательности описаний для каждого блока:

- заголовок блока;

1 Более того, в большинстве современных языков программирования вообще нет деления на процедуры и функции (например в C существуют только функции, а процедурой можно назвать функцию не возвращающую значения (void)). Даже в Pascal существует возможность настройки компилятора таким образом, чтобы не существовало различий между процедурами и функциями.

-описание констант;

-описание типов;

-описание переменных;

-внутренние блоки.

Таким образом, структура у подпрограмм такая же, как и у основной программы, за исключением того, что в подпрограмме нельзя описывать список используемых библиотек, а после операторов подпрограммы стоит end с точкой с запятой, тогда как программа заканчивается end с точкой.

Как отмечалось выше, в языке Pascal два вида подпрограмм: процедуры

и функции.

Функция – подпрограмма языка Pascal, реализующая некоторый алгоритм, результатом которого является формирование некоторого единственного значения. Обращение к функции происходит через ее имя. Функция всегда возвращает, как минимум, один параметр, причем возвращение параметра происходит через операцию присваивания, путем помещения имени функции справа от этой операции. Функции Pascal очень похожи на обычные функции, используемые в математике. Часть функций уже изначально встроена в базовый набор языка и рассматривалась ранее.

Это, например, sin(x), cos(x), ln(x), pi, frac(x), trunc(x). Видно, что у перечисленных функций есть аргумент, но не у всех. Так, функция pi его не имеет, поскольку число Пи является фундаментальной константой и ни от чего не зависит. Хоть здесь они и не представлены, однако существуют функции с числом аргументов более одного.

Стандартные функции языка Pascal представляют собой некоторый алгоритм, реализующий последовательность действий с максимальной оптимальностью. Так, например, арифметико-логическое устройство микропроцессоров не может напрямую реализовать вычисление функции sin, потому, на первом этапе sin раскладывается в ряд, что позволяет используя только базовые арифметические операторы (+, –, *, / ) вычислять сложные тригонометрические функции. Естественно, что нам не нужно заботиться о программировании этих рядов, поскольку, в виду частоты использования, их уже описали авторы базовых библиотек Pascal. Потому работа с этими функциями достаточно проста. Однако, если бы в базовый набор не был встроен sin, то, вспомнив, что разложение синуса в ряд имеет вид:

мы бы могли написать функцию: function sin(x:real):real; var xx,S:real;

i:byte;

f:longInt; begin

S:=0;

f:=1;

xx:=x;

i:=1;

while i<20 do begin

S:=S+xx; {добавление в сумму неч. члена с плюсом} i:=i+1; {четное значение}

xx:=xx*x; {четная степень} f:=f*i; {четный факториал} i:=i+1; {нечетное значение} xx:=xx*x; {нечетная степень} f:=f*i; {нечетный факториал}

S:=S-xx; {добавление в сумму неч. члена с минусом} end;

sin:=S;

end;

Здесь для простоты понимания принципа работы функции, мы ограничились первой двадцаткой членов ряда. Кроме того, здесь учтено, что период повтора знака у членов равен четырем (четные члены в сумму не включаются, однако используются для вычисления нечетных).

Далее рассмотрим порядок обращения к функциям, или, как принято говорить «вызов». Совершенно естественной выглядит запись обращения:

y:=sin(x);

z:=exp(y);

в то время, как такая запись бессмысленна: sin(x) := y; (! не верно!)

exp(y) := z; (! не верно!)

Синтаксис Pascal не допускает подобных общений. Всегда имя функции ставится справа от операции присваивания. Единственным исключением является определение значения функции при ее описании в собственном теле. Т.е. при описании для задания значения мы имя функции без параметров ставим слева от операции присваивания.

Описание состоит из заголовка и тела. Заголовок выглядит следующим образом:

function имя_функции (список формальных параметров) : тип результата;

Здесь:

имя_функции – идентификатор пользователя, используемый затем для ее вызова;

список формальных параметров – набор параметров, состоящий для функции, как правило, только из входных переменных. Для каждого формального параметра указывается его тип и способ передачи. Параметры одного типа и с одинаковым способом передачи, перечисляются через запятую, все остальные через точку с запятой.

Результат работы функции возвращается в вызывающий модуль через ее имя. Тип результата указывается в заголовке. Чтобы вернуть результат, необходимо чтобы в разделе операторов (теле) функции присутствовал хотя