Информатика_всем
.pdf



78 |
4.2 Задачи на использование циклов |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
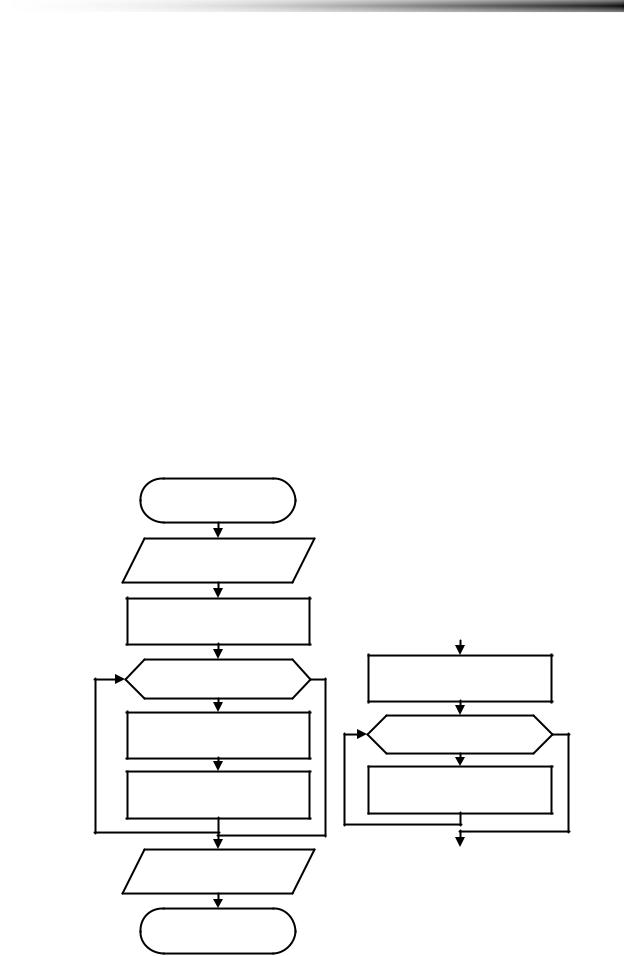
Рисунок 4.8 Поиск максимума среди значений |
функции |
действия до тех пор, пока все точки не будут рассмотрены. Описанный алгоритм представлен на (Рисунок 4.8).

4. Решение типовых задач на развилки и циклы |
79 |
Программа такова: program maxF;
var x,y,max,Xmax:real; begin
cls; x:=-1;
max:=-2*x*x*x+5*x*x+3*x-1; Xmax:=x;
while x<=4 do begin
y:=-2*x*x*x+5*x*x+3*x-1; if y>max then
begin max:=y; Xmax:=x;
end;
x:=x+0.1;
end;
writeLn('максимум достигается в точке ', x:6:2); writeLn('и он равен ',max:10:5);
end.
В результате получается, что программа нам выведет такой результат:
максимум достигается в точке 4.00
и он равен |
9.03200 |
что, судя по графику, соответствует истине.
А теперь усложним задачу таким образом, чтобы функция, которую придется табулировать, имела пару аргументов. Итак,
ПРИМЕР
Протабулировать функцию z = cos(y sin (x3 )), причем вывести только
те точки, которые больше чем 0,6 . Переменная y меняется на интервале [−2;1] с шагом y =1, переменная x меняется на интервале [13;15] с шагом x = 0,8 .
Эта задача решается в два цикла, причем один будет вложен в другой. Пусть цикл по y будет внешним, а цикл по x – внутренним. Это означает,
что мысленно зафиксировав значение y мы изменяем весь диапазон значений
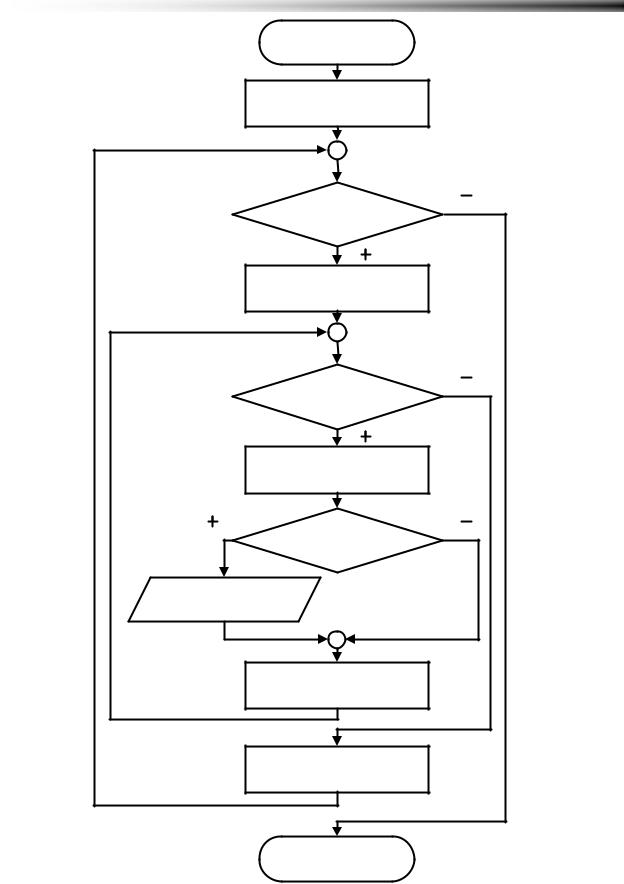
x . По своей сути изменение внутреннего цикла представляет простую табуляцию функции с одной переменной. Когда перебор всех значений переменных во внутреннем цикле окончен, мы меняем на значение шага переменную внешнего цикла и снова проходим по всем значениям цикла внутреннего. Действия повторяем до тех пор, пока не будет пройден весь диапазон изменения внешней переменной. Описанный алгоритм зафиксирован на (Рисунок 4.9).

4. Решение типовых задач на развилки и циклы |
81 |
program ddd; var x,y,z:real; begin
writeLn('табуляция функции cos(y*sin(x*x*x)):'); y:=-2;
while y<=1 do begin
x:=13;
while x<=15 do begin
z:=cos(y*sin(x*x*x)); if z<0.6 then
writeLn('z(',x:6:3,', ',y:6:3,') =',z:6:2); x:=x+0.8;
end;
y:=y+1;
end;
end.
В результате на консоли появится сообщение:
табуляция функции cos(y*sin(x*x*x)): z(13.000, -2.000) = -0.14
z(13.800, -2.000) = -0.40 z(14.600, -2.000) = -0.28 z(13.800, -1.000) = 0.55 z(13.800, 1.000) = 0.55
Рассмотрим еще одну интересную задачу.
ПРИМЕР
Для функции y =ex / x2 где x изменяется от точки x =1 с шагом x = 0,5 в положительном направлении, определить на каком шаге будет выполнено условие y >104 .
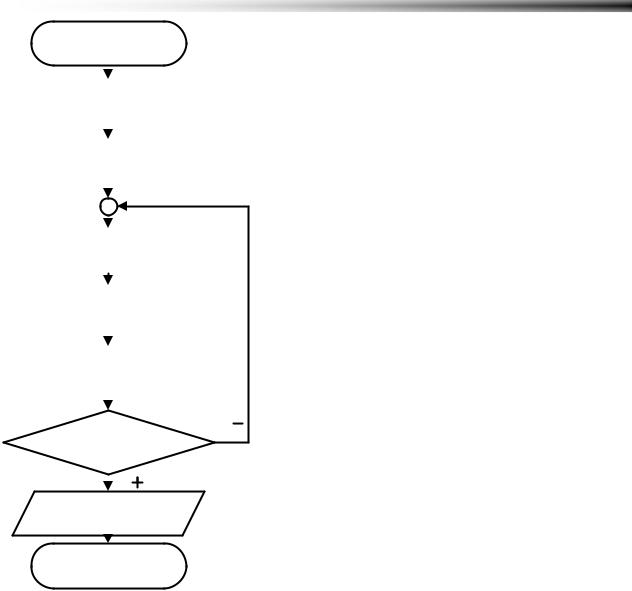
Решение задачи достаточно простое и представлено на блок-схеме
(Рисунок 4.10).
Программная реализация: program ddd;
var x,y:real; k:integer;
begin
x:=1; k:=0; repeat
y:=exp(x)/sqr(x);
inc(k);
x:=x+0.5; until y>1e4;
writeLn('условие достигается в точке ', x:8:1); writeLn('на ',k,'-м шаге' );
end.
82 4.2 Задачи на использование циклов
|
Начало |
|
В результате получим такой ответ: |
|||||||||
|
|
|
|
|||||||||
|
|
|
|
условие |
достигается |
в |
точке |
|||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
x := 1 |
|
15.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
на 29-м шаге |
|
|
|
|
||||
|
|
|
|
Как |
уже |
отмечалось |
ранее, |
при |
||||
|
k := 0 |
|
||||||||||
|
|
программировании |
циклов |
важную |
роль |
|||||||
|
|
|
|
|||||||||
|
|
|
|
играют рекуррентные формулы, которые |
||||||||
|
|
|
|
достаточно |
просто |
|
позволяют получить |
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||
|
y := ex/x2 |
|
значение |
|
элемента |
|
некоторой |
|||||
|
|
|
|
последовательности |
методом |
вычисления |
||||||
|
|
|
|
всех ее членов начиная с первого и |
||||||||
|
|
|
|
|||||||||
|
k := k + 1 |
|
заканчивая тем, который нам необходим в |
|||||||||
|
|
|
|
конкретной |
|
задаче. |
Эти |
формулы |
||||
|
|
|
|
использовались абсолютно во всех задачах на |
||||||||
|
|
|
|
|||||||||
|
x := x + 0.5 |
|
циклы, которые здесь были рассмотрены. |
|||||||||
|
|
|
|
Напомним, что рекуррентной называется |
||||||||
|
|
|
|
|||||||||
|
|
|
|
такая последовательность, у которой каждый |
||||||||
|
y > 104 |
|
последующий ее член основан на значении |
|||||||||
|
|
|
|
предыдущего. |
Это |
означает, |
что |
|||||
|
|
|
|
рекуррентными будут, в частности, все те |
||||||||
|
|
|
|
|||||||||
|
Вывод x, k |
|
операции присваивания, у которых слева от |
|||||||||
|
|
операции стоит |
переменная |
встречающаяся |
||||||||
|
|
|
|
справа. Наиболее часто используемая форма |
||||||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
Конец |
|
рекуррентной записи – это форма |
|||||||||
|
|
|
|
рекуррентного подсчета суммы. В задачах на |
||||||||
|
Рисунок 4.10 Поиск шага на |
табуляцию |
таковой |
формой |
обладают |
|||||||
котором монотонная функция |
действия |
по |
изменению |
аргумента ( |
||||||||
|
превысит некоторый порог |
x := x + |
x ). Изменение значения переменной |
|||||||||
инкрементацией. Если |
|
по |
такой |
|
формуле |
называют |
||||||
переменная |
не |
увеличивается, |
а уменьшается |
|||||||||
(используется формула |
x := x − |
x ), то действие зазывается декрементацией. |
||||||||||
Стоит отметить, что даже поиск максимума, по своей сути рекуррентен, поскольку каждое последующее его значение основано на предыдущем (хотя и не так явно, как в операциях присваивания).
Практически всегда, когда производят расчет суммы, за начальное значение принимают ноль. Рассмотрим, например, такую задачу:
ПРИМЕР
6
Найти значение суммы S = ∑k 2 . Расписывается эта сумма достаточно
k =1
просто S =12 + 22 +32 + 42 +52 +62 . В результате будем иметь 91. Блок схема изображена на (Рисунок 4.11 а)).

|
|
4. Решение типовых задач на развилки и циклы |
83 |
|||||||||
|
|
Начало |
|
|
Начало |
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
ввод N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
S := 1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P := 1 |
|
|
|
|
|
k := 1 , 6 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k := 1 , N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
S := S+k2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P := P*2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
вывод S |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
вывод P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Конец |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
|
|
Конец |
б) |
|||
Рисунок 4.11 Задачи на поиск суммы (а)) и произведения (б))
program SumS; var s:real;
k,N:integer; begin
s:=0;
for k:=1 to 6 do s:=s+sqr(k);
writeLn('сумма равна ', s:8:2); end.
При решении задач на произведения в качестве начального значения принимают 1.
ПРИМЕР
Найти значение выражения P = 2N не используя операцию возведения в
N
степень. Эта задача эквивалентна расчету такой формулы: ∏2 = 2 2 2 ... 2
k =1
(всего N двоек). Решение показано на (Рисунок 4.11 б)). program PrP;
var k,N:integer; P:longInt;
begin
writeLn('введите N'); readLn(N);
p:=1;