
Информатика_всем
.pdf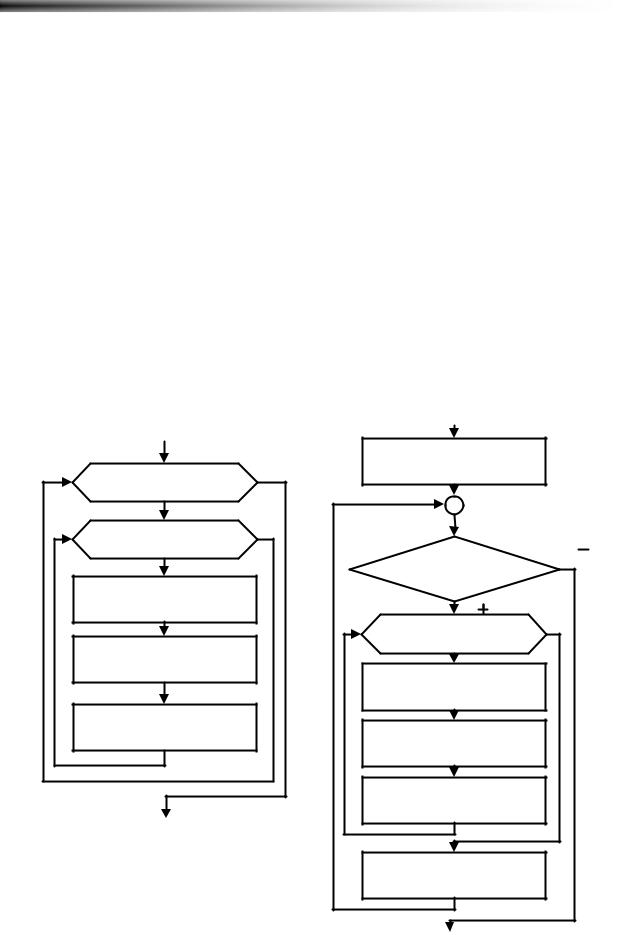
146 |
6.4 Квадратные матрицы |
6.4 Квадратные матрицы
Достаточно интересным и важным классом двумерных массивов являются квадратные. Квадратные матрицы – это такие матрицы у которых число элементов в строке равно числу элементов в столбце, т.е. M=N.
В квадратных матрицах выделяют некоторые особенные группы элементов. Это, прежде всего, главная и побочная диагонали.
Особенностью элементов на главной диагонали является тот факт, что для каждого из них индекс строки равен индексу столбца, т.е. i=j. Если внимательно посмотреть на (Рисунок 6.17), то можно вывести правило принадлежности элемента к побочной диагонали. Это правило можно выразить формулой для индексов j=N-i+1.
Для матрицы изображенной на (Рисунок 6.17) это действительно так. Покажем это:
|
N = 4 => |
|
|
|
|
|
|
A[1,4](i=1, j=4) j=4-1+1=4 |
|
|
|
|
|
|
A[2,3](i=1, j=4) j=4-2+1=3 |
|
|
|
|
|
|
A[3,2](i=1, j=4) j=4-3+1=2 |
|
|
|
|
|
|
A[4,1](i=1, j=4) j=4-4+1=1 |
|
|
|
|
|
|
Если смотреть на |
элементы |
|
|
|
|
диагоналей, то видно что они похожи |
|
|
|
|
||
|
|
|
|
|||
на |
одномерные |
массивы, |
|
|
|
|
расположившиеся вдоль |
диагоналей. |
|
|
|
|
|
Потому для их обработки достаточно |
Рисунок 6.17 Диагонали в матрице |
|||||
одного цикла. |
|
|
|
|
|
|
ПРИМЕР
Найти среднее арифметическое отрицательных элементов главной диагонали.
Решение таково (Рисунок 6.18): k:=0; S:=0;
for i:=1 to N do if A[i,i]<0 then
begin k:=k+1;
S:=S+ A[i,i]; end;
if k<>0 then begin
SrA:=S/k; writeLn(‘SrA =’, SrA:8:2); end
else
writeLn(‘На гл. диагонали нет отриц. элементов’);
|
|
6. Двумерные массивы |
147 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 6.18 Среднее арифметическое отрицательных элементов гл. диагонали
А теперь рассмотрим такую задачу:
ПРИМЕР
Обменять элементы главной и побочной диагоналей местами. Обмен происходит следующим образом:
|
4 |
2 |
8 |
9 |
|
9 |
2 |
8 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
вход: A = |
3 |
6 |
0 |
1 |
выход: A = |
3 |
0 |
6 |
1 |
|
6 |
7 |
8 |
0 |
6 |
8 |
7 |
0 |
|||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
3 |
2 |
1 |
|
1 |
3 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
148 |
6.4 Квадратные матрицы |
Алгоритм простой (Рисунок 6.19): for i:=1 to N do
begin buf := A[i,i];
A[i,i] := A[i ,N-i+1]; A[i ,N-i+1] := buf;
end;
Далее к особенным элементам стоит отнести верхний и нижний треугольники.
Нижним треугольником называют главную 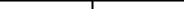 диагональ и элементы под нею. Верхним треугольником называют главную диагональ и
диагональ и элементы под нею. Верхним треугольником называют главную диагональ и  элементы над нею. Треугольники в матрице
элементы над нею. Треугольники в матрице 
показаны на Ошибка! Источник ссылки не найден..
Условие нахождения элемента в нижнем треугольнике такое: i≥j. Для верхнего треугольника неравенство обратное: i≤j.
Кроме элементов над и под главной, выделяют также элементы над и под побочной диагональю. Условие нахождения над побочной диагональю такое: j<N-i+1, а под побочной такое: j>N-i+1.
|
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
2,1 |
2,2 |
2,3 |
2,4 |
2 |
2,1 |
2,2 |
2,3 |
2,4 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
3 |
3,1 |
3,2 |
3,3 |
3,4 |
3 |
3,1 |
3,2 |
3,3 |
3,4 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
4 |
4,1 |
4,2 |
4,3 |
4,4 |
4 |
4,1 |
4,2 |
4,3 |
4,4 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
i≥j i≤j
Рисунок 6.20 Верхний и нижний треугольники в матрице
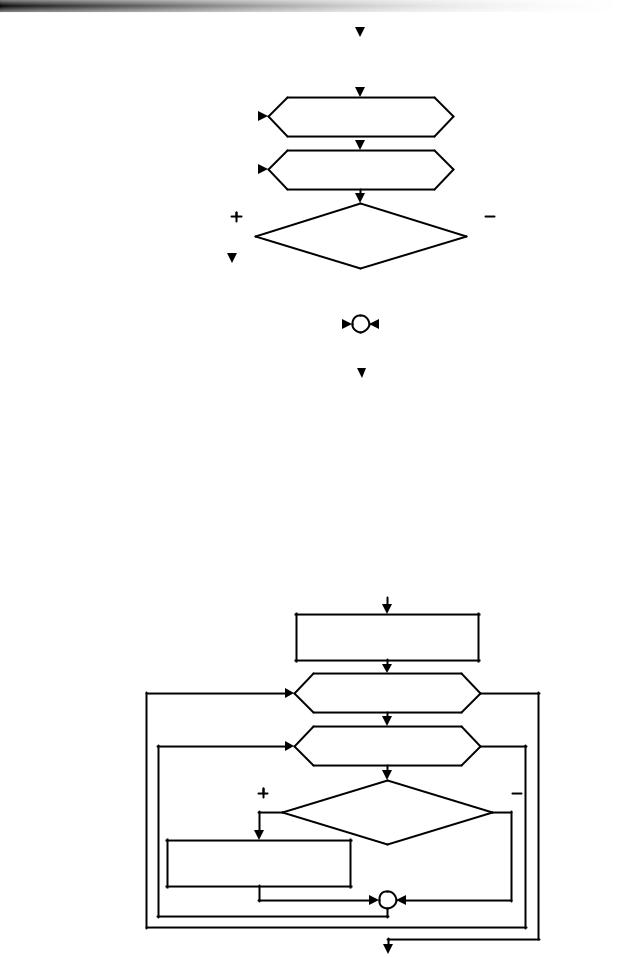
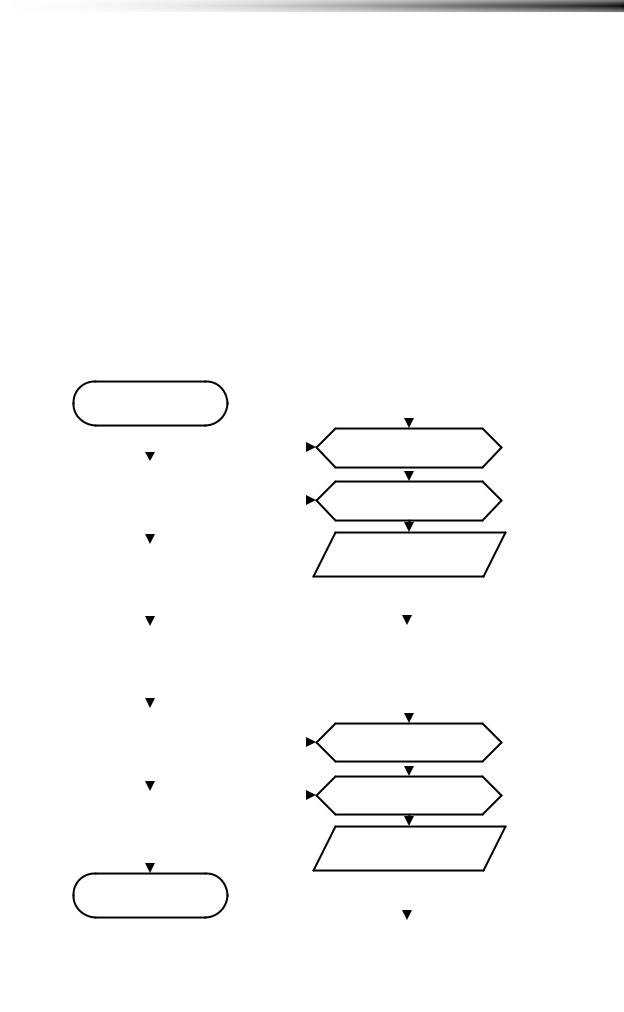
Для обработки элементов из треугольников матриц можно пользоваться двумя способами. Первый заключается в просмотре всех элементов с последующей проверкой условия принадлежности индексов элемента тому или иному треугольнику. Такой способ более надежен, однако зря расходует системные ресурсы, просматривая всю матрицу целиком. Треугольник – это примерно половина матрицы. Для более рационального использования ресурсов можно иначе задать границы изменения циклов. Однако, в этом случае есть риск ошибиться и тогда задача будет решена вообще неправильно.

6. Двумерные массивы |
151 |
program ZeroMax; const L=10;
type T2Mx = array[1.. L,1..L] of integer; var A: T2Mx;
i,j,N,M:byte;
Max:integer; begin
{шаг 1-2: ввод матрицы} writeLn('Введите размерность матрицы:'); readLn(N);
for i:=1 to N do for j:=1 to N do
begin write('A[',i,',',j,']='); readLn(A[i,j]);
end;
{шаг 2-3: вывод матрицы до преобразования} writeLn('Матрица до преобразования:'); for i:=1 to N do
begin
for j:=1 to N do write(A[i,j]:4);
writeLn;
end;
{шаг 3-4: поиск максимума} Max:=A[1,1];
for i:=1 to N-1 do for j:=1 to N-i do
if A[i,j]>Max then Max:=A[i,j];
writeLn('Max =', Max);
{шаг 4-5: замена} for i:=1 to N do for j:=1 to N do
if A[i,j]=0 then A[i,j] := Max;
{шаг 5-6: вывод матрицы после преобразования} writeLn('Матрица после преобразования:'); for i:=1 to N do
begin
for j:=1 to N do write(A[i,j]:4); writeLn;
end;
end.
152 |
6.4 Квадратные матрицы |
|
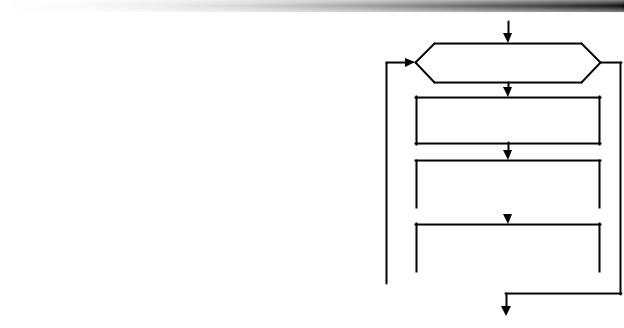
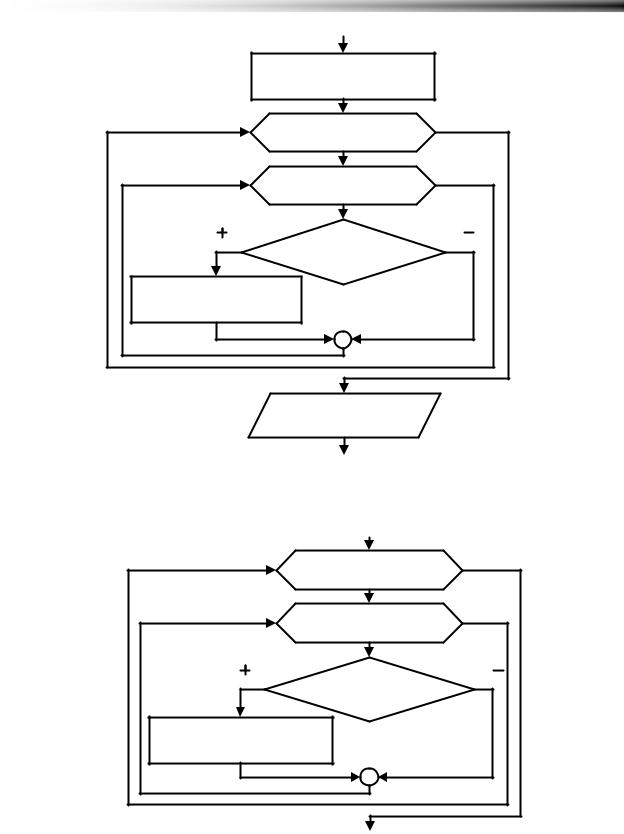
Шаг 3-4 Поиск Max |
|
Max := A[1, 1] |
|
i := 1 , N-1 |
|
j := 1 , N-i |
|
A[i, j]>Max |
|
Max:=A[i, j] |
Вывод Max
Рисунок 6.24 Поиск максимума над побочной диагональю |
Шаг 4-5 Замена нулей |
i := 1 , N |
j := 1 , N |
A[i, j]=0 |
A[i, j] := Max |
Рисунок 6.25 Замена нулей найденным максимумом |
Стоит отметить, что помимо квадратных матриц достаточно часто используют другие, более экзотические их виды. Это, например, треугольные (т.е. такие матрицы у которых число элементов в строке/столбце зависит от того в каком столбце/строке оно содержится). Есть еще разреженные матрицы, т.е. такие у которых не все ячейки заполнены элементами и т.д.
|
|
|
|
6. Двумерные массивы |
153 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
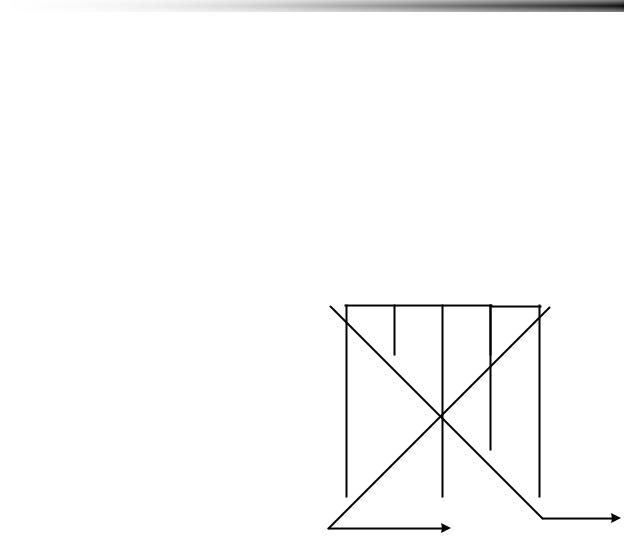
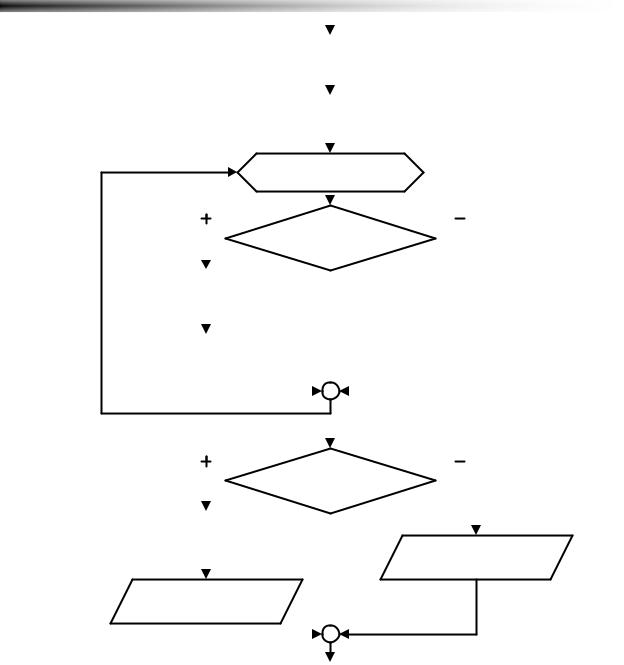
Рисунок 6.26 Удаление строки и столбца из матрицы
6.26 Удаление строки и столбца из матрицы
Среди прочего, может быть интересен алгоритм для решения такой задачи (хотя он и не относится к квадратным матрицам):
ПРИМЕР
Удалить из матрицы строку и столбец содержащие максимум всей матрицы.
Вот что требуется сделать:
|
1 |
|
2 |
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
5 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
вход: |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
|
30 |
|
|
9 |
|
|
, Imax=3; Jmax=4; выход: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
7 |
8 |
9 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
|
14 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
15 |
16 |
17 |
19 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
15 |
|
|
16 |
|
17 |
|
|
18 |
|
|
19 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Блок-схема алгоритма без программной реализации показана на Рисунок 6.26. Здесь не приводится стандартный поиск максимума. Считается, что координаты максимума Imax и Jmax были найдены ранее.
6.5 Линейная алгебра и матрицы
Матрицы широко применяются в математике и технике, а потому автоматизация процесса основных алгоритмов применяемым к матрицам будет весьма полезна. Подобно тому, как мы рассматривали основы линейной алгебры для одномерных массивов (векторов), рассмотрим основные операции для двумерных (матриц). В основе работы всех алгоритмов на матрицах лежат поэлементные операции.

