Информатика_всем

readLn(N); S_ext:=0;

for k:=1 to N do begin

S_int:=0;

for j:=k to 2*k do S_int:=S_int+cos(j);

S_ext:=S_ext+k*S_int; end;

writeLn('сумма равна ', S_ext:8:2); end.

Иногда, несмотря на кажущуюся сложность, задача решается несколько проще, чем полагалось изначально.

ПРИМЕР

Найти значение суммы S = ∑N k 2 .

k =1 k!

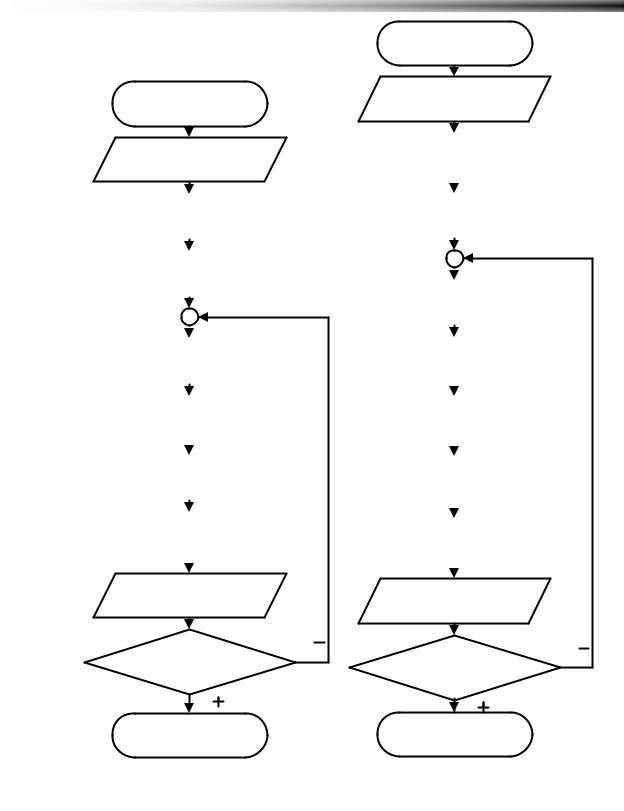
Здесь для подсчета внешней суммы потребуется на каждой новой итерации вычислять факториал для текущего значения k . На первый взгляд, без вложенного цикла на произведение не обойтись. Однако, если посмотреть внимательно на формулу и вспомнить замечательное свойство факториала заключающееся в том, что для вычисления последующего значения достаточно знать предыдущее, то алгоритм запишется намного короче (Рисунок 4.13 а)). И, что самое главное, без вложенных циклов.

На комбинацию program ddd; var s:real;

f,k,N:integer; begin

cls; writeLn('введите N'); readLn(N);

s:=0;

f:=1;

for k:=1 to N do begin

f:=f*k;

s:=s+sqr(k)/f;

end;

writeLn('сумма равна ', s:8:2); end.

ПРИМЕР

Найти значение выражения x + x + x +... (всего 20 корней).

Для вычисления этого выражения необходимо самостоятельно придумать рекуррентную формулу. Это уже будет и не сумма и не произведение, а нечто более сложное. Чтобы понять, какая формула здесь

S := S + k2/f

Вывод S

Вывод S

Конец

Рисунок 4.13 Сложная сумма - а) и нестандартная рекуррентная формула - б)

применяется, можно последовательно начать расписывать вычисляемое значение на каждом шаге. Итак,

начальное значение, достаточно просто составить алгоритм для вычисления

S (Рисунок 4.13 б)).

Программа представлена ниже: program sqrtS;

var k:integer; x,s:real;

begin cls;

writeLn('введите x'); readLn(x);

s:=0;

for k:=1 to 20 do s:=sqrt(x+s);

writeLn('s равно ', s); end.

При x=30 сумма получается равной 6, а, например, при x=7, она становится такой: 3.19258240356725.

Весьма интересными являются задачи на перекрестные рекуррентные зависимости. Перекрестными рекуррентными зависимостями называют такие, у которых каждое последующее значение вычисляется на основе нескольких предыдущих значений. Самый простой пример – это авторегрессионные последовательности. Наиболее известная последовательность задаваемая рекуррентно на основе двух предыдущих значений является последовательность Фибоначчи. Последовательность задается таким образом: a1 =1 , a2 =1, a3 = a1 + a2 , a4 = a3 + a2 , ak = ak −2 + ak −1 .

ПРИМЕР

Вывести 10 первых членов последовательности Фибоначчи.

Решается задача в один цикл. Решение представлено на (Рисунок 4.14

а)).

Ниже идет программа: program ddd;

var ak_3,ak_2,ak_1,ak:real; k:integer;

begin ak_2:=1; ak_1:=1; k:=2;

writeln(1:5,' z=',ak_1); writeln(2:5,' z=',ak_2); repeat

ak:=ak_1+ak_2; ak_2:=ak_1; ak_1:=ak; inc(k);

writeln(k:5,' z=',ak); until k=10;

end.

8z=21

9z=34

10z=55

Можно несколько модифицировать предыдущую последовательность и сделать так, чтобы в авторегрессионной формуле участвовало три предыдущих члена.

ПРИМЕР

Вывести N ( N ≤3 ) первых членов последовательности заданной рекуррентно ak = ak −1 + ak −2 + ak −3 , a1 =1 , a2 = 2 , a3 =3.

При решении этой задачи важно понять суть перехода от пары переменных к трем. В алгоритме на каждой итерации применяется так называемый циклический сдвиг переменных. Т.е. переменные принимают значения тех, которые им предшествуют. Ну а самая последняя, т.е. текущая переменная принимает свое значение согласно заданной рекуррентной формуле (Рисунок 4.14 б)). Имена переменным даны согласно порядку их расположения в последовательности, т.е. ak = ak , ak −1 = ak _1, ak −2 = ak _ 2 ,

ak −3 = ak _ 3 . Программа такова:

program ddd;

var ak_3,ak_2,ak_1,ak:real; k,N:integer;

begin

writeLn('введите N'); readLn(N);

while N<=3 do begin

writeLn('введите N'); readLn(N);

end; ak_3:=1; ak_2:=2; ak_1:=3; k:=3;

writeln(1:5,' z=',ak_3); writeln(2:5,' z=',ak_2); writeln(3:5,' z=',ak_1); repeat

ak:=ak_1+ak_3+ak_2; ak_3:=ak_2; ak_2:=ak_1; ak_1:=ak;

inc(k);

writeln(k:5,' z=',ak); until k=N;

end.

а во внутреннем – многократный вывод числа соответственно номеру строчки. Блок схема показана на Рисунок 4.15 а). Язык Pascal вот такой:

program BAC;

var i,j,N,k:integer; begin

writeLn('введите N'); readLn(N);

k:=1;

for i:=1 to N do begin

for j:=1 to i do write(k:5);

writeLn;

inc(k);

end;

end.

В результате мы увидим на консоли:

ПРИМЕР

Ввести число N, выяснить сколько раз цифра 3 входит в запись этого числа.

Алгоритм основан на последовательном рассмотрении остатка от деления на 10 младшего разряда рассматриваемого числа. Алгоритм представлен на (Рисунок 4.15 б)). Здесь переменная y хранит число равное целой части от деления текущего числа на 10. Переменная y1 – буферная переменная для хранения предыдущего (неделенного на 10) числа. Соответственно, остаток от деления проверяется для чисел y*10 и y1. Если остаток равен 3, то мы производим инкрементацию переменной k, в которой хранится количество встреченных троек.

program cifra3;

var x,y,y1,k,N:integer; begin

writeLn('введите N'); readLn(N);

y:=N;

while y>0 do begin

y1:=y;

y:=y1 div 10;

x:= (y1-y*10) mod 10; if x=3 then

inc(k);

end;

writeLn('цифра3 вх. в число ',N,'всего ',k,' раз'); end.

Вот что будет на консоли в результате работы программы:

введите N 3331333

цифра 3 вх. в число 3331333 всего 5 раз

ИмяПеременной: array [от..до] of ТипЭлементов;

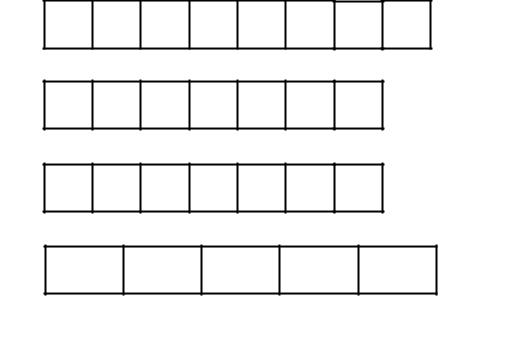
Пример объявления массивов, изображенных на рисунке (Рисунок 5.1) запишем ниже

Var

A:array [1..8] of byte;

B:array [1..7] of real;

C:array [1..7] of boolean;

D:array [1..5] of string;

Здесь представлены переменные типа «массив», которые имеют в своем составе ровно столько элементов, сколько заявлено на рисунке (Рисунок 5.1). Однако, объявление переменной есть процесс выделения под нее памяти. Еще до начала работы программы мы должны знать, какого размера массив нам потребуется в процессе ее исполнения. К сожалению, не всегда заранее известно о точной его длине. Потому приходится использовать динамические массивы (которых мы пока касаться не будем), иные эвристические подходы или просто избыточное выделение памяти.

Избыточное выделение памяти есть действие, направленное на резервирование памяти достаточной для хранения наибольшего из предполагаемых массивов в процессе выполнения программы. Так, например, если нам нужно объявить переменную, в которой будут храниться средние рейтинговые оценки академической группы студентов в 100-бальной шкале, то логичным будет длину массива ограничить 40-ка элементами, поскольку, практически не встречается групп, состоящих более чем из 40-ка человек. Хотя реально может использоваться, скажем, 25 из 40 ячеек. Остальные ячейки просто будут занимать память и не использоваться. В итоге программа становится более массовой, т.е. менее чувствительной к качеству входных данных. К сожалению, в программировании, как и в других отраслях деятельности человека, часто приходится идти на компромиссы.

Кроме прямого объявления можно использовать объявление через вспомогательный раздел type. Приведем пример такого объявления для массивов изображенных на рисунке (Рисунок 5.1).

Const

LengthA = 40;

LengthB = 50;

LengthC = 120;

LengthD = 40;

A:T1mByte;

B:T1mRe;

C:T1mBool;

D:T1mStr;