Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

KonspektElektrotekhnika_i_elektronika

.pdf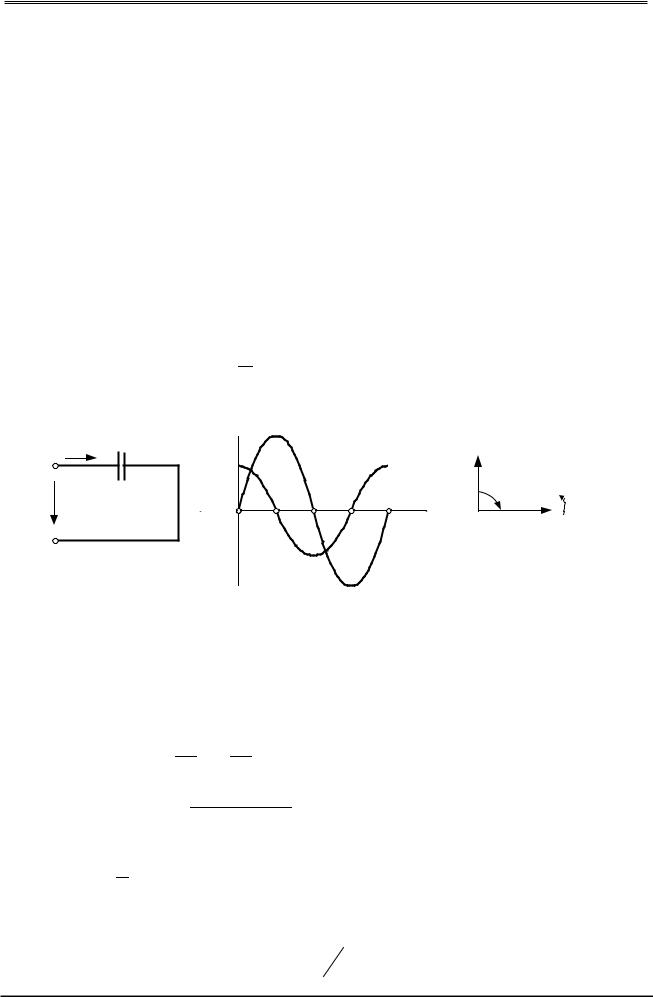

Скачиваний:

Добавлен:

03.03.2016

Размер:

6.68 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

Электротехника и электроника

2.3.3. Поверхностный эффект

Причина явления, получившего название «поверхностный эффект» (п.2.3) кроется в том, что при переменном электрическом токе части проводника рас- положенные ближе к оси охватываются большим магнитным потоком, величи- на которого уменьшается по мере удаления от оси к поверхности. Но чем меньше магнитный поток, тем меньше индуктивность и индуктивное сопротив- ление. Поэтому плотность тока неодинакова в различных точках поперечного сечения проводника: у поверхности проводника она получается больше, чем при постоянном токе, а в центре – меньше. Переменный ток как бы вытесняется к поверхности провода.

Разница в плотностях тока у оси и на периферии провода возрастает с уве- личением диаметра провода, проводимости материала, его магнитной прони- цаемости и частоты переменного тока.

Отношение активного сопротивления проводника r к его сопротивлению R при постоянном токе (омическому сопротивлению) называется коэффициентом

поверхностного эффекта ξ = r .
			R
2.3.4. Цепь с емкостным элементом
i	С	u, i		u
			i				I	ϕ=− 900	ω
u			i			ω t		ϕ=− 900

		0	π/2	π	2π
		0	π/2	π	2π				U
	a)			б)				в)
				Рис. 2.15
В цепь с напряжением u = Um sin ωt включен конденсатор. В схеме замеще-
ния (рис. 2.15,а) он представлен емкостным элементом с емкостью С. Конден-
сатор периодически заряжается и разряжается, то есть в цепи протекает пере-
менный ток:

i = dq = С du , где q = C·u - величина заряда. dt dt

Тогда: i = С d (U m sin ω t) = Сω U m cos ω t или i= Im sin (ωt+90о), dt

где амплитуда тока:

Im = Um ωC.

Разделив на 2 амплитуды тока и напряжения, получим выражение закона Ома для действующих значений:

I = ωCU =	U	=	U	,
	1
			X С
	ωC

- 30 -

					2. Однофазные электрические цепи

где ХС	=	1	=	1	- емкостное сопротивление [Ом].
где ХС	=		=	2πfС	- емкостное сопротивление [Ом].
		ωС		2πfС

Ток изменяется синусоидально (временная диаграмма - рис. 2.15,б).

Начальная фаза тока	ψi	=	π	= 90o .

		2
Угол сдвига фаз	ϕ = ψu − ψi				= −	π	,

					2

то есть напряжение отстает от тока на 90º. Векторная диаграмма напряжения и тока представлена на рис. 2.15,в.

Мгновенная мощность:

p = ui = U		I		sin ω t cosω t = I U		sin 2ω t	= UI sin 2ω t
	m		m		m
				m		2

изменяется синусоидально с частотой, вдвое большей частоты переменного то- ка (рис. 2.16). Мгновенная мощность положительна, пока возрастает напряже- ние на конденсаторе - конденсатор заряжается;

	р		происходит накопление энергии в его электри-
	u		ческом поле. Когда напряжение понижается,
	u		конденсатор разряжается на источник, то есть
		i	конденсатор разряжается на источник, то есть
		i	энергия из электрического поля возвращается
			энергия из электрического поля возвращается
0	π	ω t	назад к источнику.
0	π	2π	Средняя за период (активная) мощность:
			Р = 0 .
			В цепи происходит обмен энергией между
			источником и приемником. Эта энергия харак-
			теризуется реактивной емкостной мощно-
	Рис. 2.16		стью:
	Рис. 2.16		QС = U·I = I2·XС, [вар].
			QС = U·I = I2·XС, [вар].
Таким образом, емкостной элемент является реактивным элементом.

Пример 2.6. Построить векторную диаграмму, найти активную мощность Р и потребление энергии емкостным приемником ХС за время работы t = 1 час, если известно U = 200 B, I = 10 A. Определить реактивную емкостную мощ-

ность.						I
Решение. Для емкостного приемника: P = 0 Вт.						I

						-90o
Потребляемая энергия W = I	2	r t = P t = 0 1 = 0	Вт·час.			-90o
Потребляемая энергия W = I		r t = P t = 0 1 = 0	Вт·час.
Угол сдвига фаз между напряжением и током ϕ = −				π	, то	U
Угол сдвига фаз между напряжением и током ϕ = −					, то	U

	2
	есть на векторной диаграмме (рис. 2.17) вектор напряжения U	Рис. 2.17
	отстает от вектора тока I на 90º:	Рис. 2.17
	отстает от вектора тока I на 90º:
	Реактивная емкостная мощность:
	QС = U·I = 200·10= 2000 Вар= 2 квар.

- 31 -

Электротехника и электроника

2.4. ЦЕПЬ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ РЕЗИСТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО ЭЛЕМЕНТОВ

В цепь с напряжением u = U m sin ωt включены последовательно соединен-

ные резистор с сопротивлением r, катушка с индуктивностью L и конденсатор с
емкостью С. В схеме замещения (рис. 2.18,а) они представлены идеальными
элементами. При прохождении тока на выводах элементов возникают напряже-
ния: ua – на резистивном элементе, uL –					на индуктивном элементе, uС – на емко-
стном элементе.			Согласно второму закону Кирхгоффа, мгновенное значение
						полного напряжения:
i	r	L	C			u = ua + uL + uС.
				UL		Ток и напряжения изменя-
				UL		ются синусоидально. Это по-
	ua	uL	uС	UC	ω	ются синусоидально. Это по-
u	ua	uL	uС	U		зволяет перейти к векторному
						зволяет перейти к векторному
						изображению величин. Дейст-
				Up		изображению величин. Дейст-
			ϕ	Ua	I	вующее значение полного на-
						пряжения U равно геометриче-
		а)		б)		ской сумме напряжений на от-
		а)		б)		дельных элементах:
			Рис. 2.18			дельных элементах:
			Рис. 2.18			U = Ua + UL + UC,
						U = Ua + UL + UC,

где Ua = I·r - активное напряжение совпадает по фазе с током I (φа = 0);

UL = I XL - индуктивное напряжение опережает ток на 90° ( φL = 90о); UC = I XC - емкостное напряжение отстает от тока на 90° ( φС = - 90о).

Для определения полного напряжения построим векторную диаграмму (рис. 2.18,б). Начинаем с вектора тока I, который является общим для всей схе- мы. Под углом 0о относительно вектора тока проводим вектор Ua, из конца ко- торого под углом φL = 90о откладываем вектор UL; из конца вектора UL под уг- лом φС = - 90о относительно вектора I проводим вектор UС. Допускаем, что XL>XC , поэтому вектор UL длиннее вектора UC. Результирующий вектор U со- единяет начало вектора Ua с концом вектора UC.

Общее напряжение на реактивных элементах называется реактивным на- пряжением U L + U C = U р . Так как векторы индуктивного и емкостного на-

пряжений имеют противоположные направления, то действующее значение ре- активного напряжения:

Uр= UL - UC .

Векторы U, Uа, Uр являются сторонами прямоугольного треугольника - треугольника напряжений, где действующее значение полного напряжения:

U = U a2 + U p2 = U a2 + (U L − UС )2 .

Активная и реактивная слагающие напряжения:

U a = U cosϕ ; U p = U sinϕ .

Угол между векторами U и Uа:		U L − UC
ϕ	U p
	= arctg	= arctg

	U a		U a

- угол сдвига фаз между напряжением U и током I.

- 32 -

2. Однофазные электрические цепи

Разделив все стороны треугольника напряжений на величину тока I, полу-

чим треугольник сопротивлений (рис. 2.19), где:

r =

U a

- активное сопротивление;

Z =

- полное сопротивление;

X =

U p

- результирующее реактивное сопротивление,

Рис. 2.19

X = XL - XC, где X L =

U L

- индуктивное сопротивление;

X C = C - емкостное сопротивление.

Таким образом, знак Х позволяет определить, является ли оно индуктив- ным или емкостным.

Из треугольника сопротивлений получим:

					; X = Z sinϕ ; r = Z cosϕ ,
		Z =	r 2 + (X L − X C )2
где ϕ = arctg	X	= arctg	X L − X C	- угол сдвига фаз межу напряжением и током.

	r		r

Величина и знак угла φ позволяют определить характер нагрузки (показы- вает, какие элементы присутствуют в эквивалентной схеме замещения):

φ > 0 – активно-индуктивная (r и L); φ < 0 – активно-емкостная (r и С); φ = 0 – активная (r); φ = 90о – индуктивная (L); φ= - 90о – емкостная (С).

Таким образом, возможны пределы изменения − π ≤ φ ≤ π в зависимости

от соотношения r, XL, XC.		2	2
от соотношения r, XL, XC.
Выражение закона Ома для этой цепи:
I =	U	= U .
r 2	+ ( X L − X C )2	Z

Пример 2.7. В цепи с последовательным соединением элементов r, L, C из- вестны U = 100 B, r = 4 Oм, XL = 5 Oм, XC = 2 Oм. Найти ток І и напряжения на выводах элементов Ur, UL, UC. Построить векторную диаграмму.

Решение. Полное сопротивление цепи:

Z = r 2 + (X L − X C )2 = 42 + (5 − 2)2 = 5 Ом.

= U = 100 =

Действующее значение тока I 20 А.

Z 5

Действующие значения напряжений на элементах:

U а = U r = I r = 20 4 = 80 В;

U L = I X L = 20 5 =100 В; UC = I X C = 20 2 = 40 В.

Для полученных значений напряжений векторная диаграмма изображена на рис. 2.18,б.

- 33 -

Электротехника и электроника

Если все стороны треугольника напряжений умножить на величину тока I,

то получим треугольник мощностей (рис. 2.20), где:

P = Ua·I - активная мощность [Вт];	S

Q = Up·I - реактивная мощность [вар];
	Q
S = U·I - полная мощность. Единица - вольт-ампер [ВА].
	ϕ P
Q = QL - QC ,

где QL = UL·I - реактивная индуктивная мощность; QC = UC·I - реактивная емкостная мощность. Из треугольника мощностей следует:


	S =			P2	+ Q2		.
Так как S = U I, а U = I·Z, то S = I2·Z.
P = S cosϕ	= UI cosϕ . Так как U·cosϕ				= Ua= I r, то
Q = S sinϕ	= UI sinϕ . Так как U·sinϕ				= Up= I Х, то
Угол сдвига фаз:						QL − QC
	ϕ = arctg	Q	= arctg					.

		P					P

Рис. 2.20

P = Ua·I= I2·r.

Q = Up·I= I2·Х.

Поскольку Q = QL - QC, то знак реактивной мощности позволяет определить, является ли она индуктивной «+» или емкостной «-». При этом соответственно угол сдвига фаз будет ϕ > 0 или ϕ < 0.

Если в цепи находится два или более последовательно соединенных одно- типных приемника, то для вычисления полной мощности нужно сначала найти суммарные активную и реактивную мощности:

		=					.
S = (∑P )2	+ (∑Q )2	=	(∑P )2	+ (∑Q	Lk	− ∑Q )2	.
k	k		k		Lk	Ck

Выражение активной мощности отличается от выражения мощности по- стоянного тока наличием множителя cos φ, называемого коэффициентом мощ-

ности:

cosϕ = P =	P	.
	P2 + Q2
S

Коэффициент полезного действия - отношение полезно используемой при- емником мощности Р2 к потребляемой им из сети мощности Р1:

η =	P	=	P − ∆ P
	2		1	,
	P		P	,
	P		P
	1		1
где потери мощности ∆P= P1 - P2.

Пример 2.8. По значениям U = 100 B, I = 10 A, ϕ = -30° определить Р, Q, S цепи. Указать характер нагрузки. Найти энергию, которую получает нагрузка за t = 30 с работы.

Решение. Полная мощность S = U I =100 10 =1000 ВА.

Активная мощность P = S cosϕ =1000 cos30o =1000	3	= 860 Вт.
	2
			1
Реактивная мощность Q = S sinϕ =1000 sin(− 30) = −1000				= −500 вар.

	2

- 34 -

2. Однофазные электрические цепи

Так как Q отрицательная, то она является емкостной мощностью. Следова- тельно, полная мощность имеет две составляющие: активную и реактивную ем- костную. Характер нагрузки: активно – емкостной.

Потребляемая электрическая энергия W = P t = 860 0,5 = 450 Вт·час.

2.4.1. Резонанс напряжений

Возникает в цепи с последовательным соединением резистивного, индук- тивного и емкостного элементов при условии:

XL = XC .

Следовательно, реактивные индуктивное UL = IХL и емкостное UС = IХС на- пряжения компенсируют друг друга UL – UС = 0. Векторная диаграмма пред- ставлена на рис. 2.21.

Полное сопротивление Z = r 2 + ( X L − X C )2 = r имеет минимальное зна-

чение.

Ток I = U = U максимален.

X L − X C

Угол сдвига фаз ϕ

= arctg

= 0,

то есть ток совпадает по фазе с

напряжением.

пряжением.

Полное

напряжение

цепи

= I r

U =

U a2 + (U L − UС )2

= U a

приложено к

актив-

ному сопротивлению.

I r

U=Ua

Из соотношений

полу-

I X

Рис. 2.21

чим

U L = UC = U

X L

= U

X C

Таким образом, если индуктивное XL и емкостное XC сопротивления цепи больше ее активного сопротивления, то напряжения на XL и XC при резонансе

напряжений превосходят приложенное к цепи напряжение в X L = X C раз, то r r

есть на участках с XL и XC возникают перенапряжения. Вследствие этого в элек- тротехнических установках может быть пробита изоляция. Например, если в кабельную линию включить последовательно катушку какого-нибудь аппарата, индуктивность которой находится в резонансном соотношении с емкостью ка- беля.

Однако во многих областях электротехники резонанс находит полезное применение. Например, в радиотехнике для усиления электрических сигналов, настройке радиоприемников на частоту передатчика.

Цепь, содержащая индуктивный и емкостной элементы, представляет со- бой колебательный контур. Если в первую четверть периода конденсатор с ем-

костью С заряжается; в электрическом поле запасается энергия W = CU m 2 .

- 35 -

Электротехника и электроника

В течение следующей четверти периода конденсатор разряжается на ка- тушку с индуктивностью L. В магнитном поле накапливается энергия

W = LI m 2 . После этого энергия магнитного поля катушки индуктивности

преобразуется в энергию электрического поля конденсатора. Таким образом, происходит непрерывный обмен энергией между индуктивным и емкостным элементами. Поступающая от источника энергия полностью преобразуется в тепловую W = r I 2t в резистивном элементе с активным сопротивлением r.

Пример 2.9. Цепь с последовательным соединением элементов r, L, C ра- ботает в режиме резонанса напряжений. Известны:

U = 100 B, Ur = 100 В, UL = 30В, І = 1 А.

Найти UС и емкостное сопротивление конденсатора.

Решение. При резонансе: U		= U		= 30 B, тогда X		=	U	С	=	30	= 30 Ом.
	L		C		C
							I		1

2.5. ЦЕПЬ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ РЕЗИСТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО ЭЛЕМЕНТОВ

В цепь с напряжением u = U m sin ωt включены параллельно соединенные

резистор с сопротивлением r,

ia iL iC

u r

L C

а)

Рис. 2.22

катушка с индуктивностью L и конденсатор с ем-

						костью С. В схеме замещения
				U	ω	(рис. 2.22,а) они представлены
ϕ		Ia			ω	идеальными элементами. Со-
						идеальными элементами. Со-
			I			гласно первому закону Кирх-
	I		I			гласно первому закону Кирх-
			р			гоффа мгновенное значение
						гоффа мгновенное значение
			IC	IL		полного тока (тока в нераз-
						полного тока (тока в нераз-
						ветвленной части цепи):
						ветвленной части цепи):
						i = ia + iL + iС,
		б)				где ia – ток в ветви с рези-
						стивным элементом, iL – ток в
						ветви с индуктивным элемен-

том, iС – ток в ветви с емкостным элементом.

Токи изменяются синусоидально, поэтому переходим к их векторному изо- бражению. Действующее значение полного тока I представляет собой геомет- рическую сумму токов отдельных ветвей:

I = I a + I L + I C ,

где

, I

- действующие значения соответственно актив-

X L

X C

ного, индуктивного и емкостного токов.

Для определения полного тока строим векторную диаграмму (рис. 2.22,б). Общим для всех ветвей является напряжение. Приняв начальную фазу ψu = 0, проводим вектор U горизонтально. Под углом φа = 0о относительно вектора U проводим вектор Ia (ток Ia совпадает по фазе с напряжением U), из конца кото- рого под углом φL = 90о относительно U откладываем вектор IL, учитывая, что ток IL отстает от U; из конца вектора IL под углом φС = - 90о относительно U

- 36 -

2. Однофазные электрические цепи

проводим вектор IC, учитывая, что ток IC опережает U. Допускаем, что XL < XC (поэтому вектор IL длиннее вектора IC). Результирующий вектор I соединяет на- чало вектора Ia с концом вектора IC.

Общий ток ветвей с реактивными элементами называется реактивным током I L + I C = I p . Так как векторы индуктивного и емкостного токов имеют

противоположные направления, то действующее значение реактивного тока:

I р= I L - I C .

Векторы I, Iа, Iр являются сторонами прямоугольного треугольника - тре-

угольника токов, где полный ток:

I = Ia2 + I p2 = Ia2 + (I L − IC )2 .

Активная и реактивная слагающие тока:

	Ia = I cosϕ		; I p = I sinϕ .
Угол между векторами I и Iа:						− I
ϕ	= arctg	I p	= arctg	I	L		C
		Ia				Ia

- угол сдвига фаз между напряжением и током.

Разделив все стороны треугольника токов на напряжение

угольник проводимостей (рис. 2.23), где:

ϕ G

Рис. 2.23

U, получим тре-

G =

- активная проводимость;

Y =

- полная проводимость;

B =

I p

- результирующая реактивная проводимость.

В= BL - BC

, где BL =

I L

– реактивная индуктивная проводимость;

X L

– реактивная емкостная проводимость.

X C

Из треугольника проводимостей следует:

G= Y·cos φ; B= Y·sin φ; Y = G 2 + B2 =

G 2 + (B

− B )2 ,

где угол сдвига фаз

BL − BC

ϕ = arctg

= arctg

Закон Ома для параллельного соединения выражается

формулой:

I = U Y .

Рис. 2.24

Если умножить стороны треугольника токов на напряже-

ние U то получим треугольник мощностей (рис. 2.24), в кото-

ром катеты треугольника изображают активную Ia·U = P и реактивную Ip·U = Q мощности, а гипотенуза — полную мощность U·I =S.

- 37 -

Электротехника и электроника

Реактивная мощность цепи Q = QL - QC имеет две составляющие: IL·U = QL

– реактивную индуктивную мощность и IC·U = QC - реактивную емкостную мощность.

Гипотенуза S и катет P образуют между собой угол φ, равный углу сдвига фаз между напряжением U и током I.

Таким образом, имеем: S = P2 + Q2 .

P = S cosϕ

= UI cosϕ ; но I cosϕ

= Ia

; тогда P = Ia

U =

U 2

Q = S sinϕ

= UI sinϕ

; но I sinϕ

= I p

; тогда Q = I p

U =

U 2

S=U I; I =

; S =

U 2

Соотношение, определяющее угол сдвига фаз: ϕ = arctg Q .

Пример 2.10. В цепи с параллельным соединением элементов r, L, C из-

вестны U = 100 B, r = 25 Oм, XL = 20 Oм, XC = 50 Oм. Определить токи І, Ir, IL, IC.

Построить векторную диаграмму.

Решение. Активный ток Iа

= I r

100

= 4 A.

r 25

Индуктивный ток I L =

100

= 5 A.

X L

Емкостный ток IC =

100

= 2 A.

X C

Общий ток I = I r2 + (I L − IC )2 = 42 + (5 − 2)2 = 5 A.

Задаемся направлением вектора напряжения, относительно которого откла- дываем вектора токов. Ток Ia совпадает по направлению с U; из конца вектора Ia откладываем вектор тока IL, который отстает от U на 90о; из конца вектора IL – вектор IС, который опережает U на 90о. Результирующий вектор соединяет на- чало вектора Ia с концом вектора IC. Для полученных значений токов векторная диаграмма соответствует рис. 2.22,б.

2.5.1. Резонанс токов

Возникает в цепи с параллельным соединением индуктивного и емкостного элементов при условии:

	U	ω			BC = BL.
			При этом реактивные токи: индуктивный IL = U·ВL и
I= I
I= I
a			емкостный IC = U·ВС, компенсируют друг друга IL – IС= 0.
			емкостный IC = U·ВС, компенсируют друг друга IL – IС= 0.
IC	I		Векторная диаграмма представлена на рис. 2.25.
	L		Полная проводимость равна активной проводимости
			Полная проводимость равна активной проводимости

			Y = G 2 + (B	L	− B )2 = G , то есть имеет минималь-
			Y = G 2 + (B		− B )2 = G , то есть имеет минималь-
Рис. 2.25					C
Рис. 2.25			ное значение.

- 38 -

2. Однофазные электрические цепи

Общий ток I также имеет минимальное значение:

I = Ia2 + (I L − IС )2 = Ia = U G

ипротекает в ветви с резистором. Угол сдвига фаз:

ϕ= arctg ВL − ВC = 0,

то есть ток совпадает по фазе с напряжением.

При резонансе токи IL, IC замыкаются в контуре, образуемом ветвями с ин- дуктивным и емкостным элементами. Они могут во много раз превосходить ток I в неразветвленной части цепи, что может быть опасно.

В цепи происходит непрерывный обмен реактивной энергией между ин- дуктивным и емкостным элементами (QC = QL). Энергия от источника покрыва-

ет только потери в ветви с активным сопротивлением ( S = P2 + Q2 = P = Ia2 r ).

Пример 2.11. В цепи с параллельным соединением элементов r, L, C из- вестны U = 100 B, Ir = 4 A, IL = 3 A. Найти ток ІC и емкостное сопротивление конденсатора, чтобы в цепи состоялся резонанс токов.

Решение. Вследствие резонанса I L = IC = 3 A. Тогда:

X C	=	U	=	100	= 33,3 Ом.

		IC 3
				2.6. КОЭФФИЦИЕНТ МОЩНОСТИ И ЕГО
				ТЕХНИКО-ЭКОНОМИЧЕСКОЕ ЗНАЧЕНИЕ

Коэффициентом мощности называют отношение активной мощности P к полной S. Численно он равен косинусу угла сдвига фаз между напряжением и током:

P = UI cosϕ = ϕ cos .

SUI

Сточки зрения рационального использования электрических машин и ап- паратов, которые служат источниками электрической энергии, желательно иметь как можно более высокий коэффициент мощности, то есть приближаю- щийся к cos φ = 1. Например, для питания приемника мощностью Р = 100 кВт при cos φ = 0,7 источник питания должен быть рассчитан на полную мощность:

S =	P	=	100	=143кВА,
	cosϕ
		0,7

а при cos φ = 1 – только на 100 кВА.

Высокий коэффициент мощности желательно также иметь для уменьшения потерь при передаче энергии по проводам ЛЭП. При мощности приемника в


конце ЛЭП P = U·I·cos φ ток						I =		P	, а мощность потерь энергии в линии:
конце ЛЭП P = U·I·cos φ ток						I =		U cosϕ	, а мощность потерь энергии в линии:
∆ P	= I 2r	=		P2			r ,
∆ P	= I 2r	=	U 2 cos2		ϕ		r ,
ЛЭП	ЛЭП		U 2 cos2		ϕ		ЛЭП

то есть чем больше cos φ, тем меньше потери в ЛЭП.

- 39 -

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.05.2019166.4 Кб10jittya_cinnist.doc
#
03.03.2016804.45 Кб20k481.pdf
#
03.03.201676.43 Кб16khuy.docx
#
03.03.2016387.96 Кб15Komponenty_sredy_Grasshopper.pdf
#
03.03.20162.51 Mб12Komunalne_pravo_metodichka.rtf
#
03.03.20166.68 Mб37KonspektElektrotekhnika_i_elektronika.pdf
#
22.11.20194.08 Mб8Konspekt_lektsiy.doc
#
01.07.20251.95 Mб0Konspekt_lektsiy_z_TsZ_04_12_2012.docx
#
03.03.20163.71 Mб40konspekt_lektsy_mikro.doc
#
03.03.2016871.94 Кб13Konspekt_po_PE_1chast.doc
#
03.03.20166.04 Mб31kpi Moy Kurcach.docx