Том-1_РУ

Электромагнетизм

где величину max NBS можно рассматривать как амплитудное значение пе-

ременной эдс.

Возникновение эдс индукции во вращающейся в магнитном поле рамке явилось основой для создания генераторов переменного тока. Если концы витка присоединить к вращающимся вместе с ним двум медным кольцам, соприкасающимся с двумя неподвижными угольными щетками, а к щеткам присоединить электрическую цепь, то по цепи потечёт переменный ток i, изменяющийся так же, как изменяется эдс ε.

По закону Ома:

где imax NBSR максимальное (амплитудное) значение силы тока; i мгновенное значение тока.

Большинство приборов, измеряющих переменный ток и переменное напряжение, показывают не мгновенные значения тока и напряжения, а действующие (эффективные) значения. Действующие значения силы тока Iд и

напряжения Uд определяются мощностью, выделяемой в цепи переменного то-

ка. Они связаны с амплитудными значениями силы тока и напряжения следующими соотношениями:

Действующие значения напряжения и тока являются важнейшими электротехническими параметрами устройств. Именно эти величины указываются в паспортах любых электроустановок и устройств.

58.3 Токи Фуко

Индукционные токи, которые возникают в сплошных массивных проводниках, находящихся в переменных магнитных полях, называют вихревыми то-

ками или токами Фуко*.

В соответствии с правилом Ленца токи Фуко выбирают внутри проводника такие направления, чтобы своим действием возможно сильнее противиться причине, которая их вызывает. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Это используют для демпфирования (успокоения) подвижных частей гальванометров, сейсмографов и др. приборов.

Тепловое действие токов Фуко используются в индукционных печах. Такая печь представляет собой катушку, питаемую высокочастотным током

________________________________________________________________________________________________________________________

*Фуко Жан Бернар Леон (1819–1868), французский физик-экспериментатор.

201

Электромагнетизм

большой силы. Если поместить внутрь катушки проводящее тело, в нем возникают интенсивные вихревые токи. Эти токи могут разогреть тело до плавления. Таким способом осуществляют плавление металлов в вакууме, это дает возможность получать материалы исключительно высокой чистоты.

Токи Фуко бывают и нежелательными. В электрических машинах и трансформаторах они приводят к значительным потерям энергии. Поэтому сердечники трансформаторов набирают из тонких пластин разделенных изолирующими прослойками. Пластины располагают так, чтобы возможные направления токов Фуко были к ним перпендикулярными.

В проводах, по которым текут переменные токи, также возникают токи Фуко. Они направлены так, что ослабляют ток внутри провода и усиливают вблизи поверхности. В результате быстропеременный ток как бы вытесняется на поверхность проводника. Это явление называется скин-эффектом (skin – кожа). Из-за скин-эффекта внутренняя часть проводников в высокочастотных цепях оказывается бесполезной. Поэтому в высокочастотных цепях применяют проводники в виде трубок.

§59 Самоиндукция

Самоиндукция это явление возникновения электродвижущей силы в

проводящем контуре при изменении электрического тока, идущего по это-

му контуру. Самоиндукция является частным случаем электромагнитной индукции. При изменении тока в контуре меняется поток магнитной индукции через поверхность, ограниченную этим контуром. В результате этого в нем возбуждается эдс самоиндукции. При увеличении в цепи силы тока эдс самоиндукции препятствует его возрастанию, а при уменьшении тока – его убыванию. Можно сказать, что самоиндукция подобна явлению инерции в механике. Из эксперимента следует, что величина эдс самоиндукции пропорциональна скорости изменения силы тока и величине, называемой индуктивностью.

59.1 Индуктивность контура

Электрический ток, текущий в проводящем контуре, создает в окружающем пространстве магнитное поле. Полный магнитный поток Ψ, пронизывающий контур (сцепленный с ним), будет прямо пропорционален току:

Коэффициент пропорциональности L между полным магнитным потоком (потокосцеплением) и силой тока называется индуктивностью контура или коэффициентом самоиндукции контура.

Индуктивность (L) это скалярная физическая величина, характеризующая магнитные свойства электрической цепи и равная отношению полного магнитного потока, сцепленного с контуром, к силе тока, текущему по контуру и создающему этот поток:

202

Линейная зависимость Ψ от I наблюдается только в том случае, если магнитная проницаемость μ среды, которой окружен контур, не зависит от напряженности поля Н. Это означает, что среда должна быть неферромагнитная. В противном случае μ сложным образом зависит от тока и, следовательно, зависимость полного магнитного потока от тока также будет довольно сложная. Однако, соотношение (59.1) распространяют и на этот случай, считая индуктивность L функцией тока I.

Из сказанного следует, что индуктивность зависит от геометрической формы и размеров контура, а также магнитных свойств среды, в которой он находится. Если контур жесткий и вблизи него нет ферромагнетиков, то индуктивность является величиной постоянной.

За единицу индуктивности в СИ принимается индуктивность такого проводника (контура), у которого при силе тока в нем 1 А возникает сцепленный с ним полный проток Ψ, равный 1 Вб. Эту единицу называют генри (Гн).

L ВбА Гн (генри*).

Индуктивность можно рассчитывать на основе геометрии проводника. Пример. Расчет индуктивности соленоида.

Возьмем соленоид такой длины, чтобы его можно было считать бесконечным. На практике это означает, что d l (рис. 59.1). При протекании по обмотке тока I внутри соленоида возбуждается однородное магнитное поле, индукция которого

B 0 In ,

где B индукция магнитного поля;

S площадь поперечного сечения соленоида.

Записанные соотношения подставим в формулу (59.2), получим:

________________________________________________________________________________________________________________________

*Генри Джозеф (1799–1878), американский физик.

203

Электромагнетизм

где lS V объем соленоида.

Из формулы (59.4) следует, что индуктивность соленоида, не имеющего ферромагнитного сердечника, пропорциональна квадрату плотности намотки витков.

59.2. Эдс самоиндукции

Самоиндукция является частным случаем явления электромагнитной индукции. Воспользуемся законом Фарадея для электромагнитной индукции (см.

формулу (58.2)):

s ddt .

Согласно (59.1) полный магнитный поток:

LI .

Если контур жесткий и вблизи него нет ферромагнетиков, то индуктивность L является величиной постоянной, и ее называют статической. В этом случае:

так как в выражении (59.7) производная индуктивности по току при этих условиях обращается в нуль: dLdI 0.

204

Электромагнетизм

Из формул (59.8) и (59.9) следует, что эдс самоиндукции пропорциональна скорости изменения силы тока. Знак « » обусловлен правилом Ленца, согласно которому индукционный ток всегда направлен так, чтобы противодействовать причине его вызывающей.

Соотношение (59.9) дает возможность определить индуктивность как коэффициент пропорциональности между скоростью изменения силы тока в контуре и возникающей вследствие этого эдс самоиндукции. Однако, такое определение правомерно лишь в случае, когда L const .

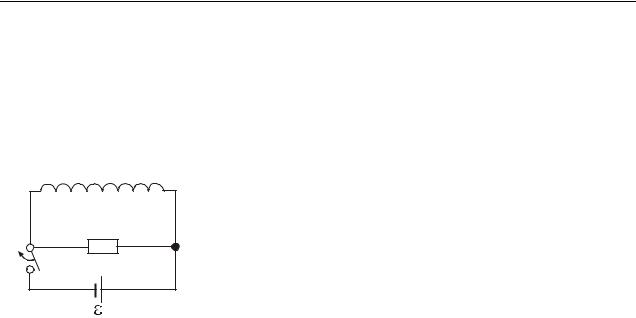
59.3 Токи при замыкании и размыкании цепи

При замыкании цепи, содержащей постоянную эдс, сила тока за счет эдс самоиндукции устанавливается не мгновенно, а через некоторый промежуток времени. При выключении источника (размыкании цепи) ток не прекращается мгновенно. Это объясняется тем, что в контуре появляется индукционный ток, который по правилу Ленца противодействует изменению тока в цепи, вызвавшего явление самоиндукции. Индукционный ток, накладываясь на основной ток, замедляет его возрастание или препятствует его убыванию.

Установим характер изменения тока в цепи, содержащей индуктивность. Будет считать, что индуктивность не зависит от тока, т.е. L const .

205

Электромагнетизм

тивность цепи и больше ее сопротивление, тем быстрее нарастает ток.

б) Размыкание цепи.

В момент времени t=0 отключим источник переключателем П (рис. 59.2). Сила тока начнет убывать, в цепи возникает эдс самоиндукции. По закону Ома:

IR s L dIdt .

Разделим уравнение на L, получим:

dIdt RL I 0 .

Решая данное линейное однородное дифференциальное уравнение (попробуйте выполнить это самостоятельно) и учтя, что при t=0 сила тока имела значение I0, получим:

Взаимной индукцией называется явление возникновения электродвижущей силы в одном из контуров при изменении тока в другом.

Рассмотрим два близко расположенных контура 1 и 2 (рис. 60.1). В контуре 1 течет ток I1, который создает магнитный поток Ф21, пронизывающий контур 2:

где L12 – коэффициент взаимной индукции контуров 2 и 1.

Взаимная индуктивность – это скалярная физическая величина, характеризующая магнитную связь двух или более контуров. Взаимная индуктивность зависит от размеров и формы контуров 1 и 2, расстояния между ними, от

206

Электромагнетизм

их взаимного расположения, а также от магнитной проницаемости окружающей их среды. Измеряется взаимная индуктивность в генри.

Согласно закону электромагнитной индукции при изменении тока I1 в контуре 2 индуцируется эдс:

Если контуры находятся в неферромагнитной среде, то L12 L21. Поэтому

можно не делать различия между L12 и L21 и просто говорить о взаимной индуктивности двух контуров.

Найдем взаимную индуктивность двух катушек, намотанных на общий тороидальный железный сердечник (рис. 60.2). Если в первой катушке N1 витков и по ней течет ток I1, то по закону полного тока (см. формулу (51.7)):

Сравнение выражения (60.8) с формулой (60.1) позволяет сделать вывод,

что

Аналогичное значение можно получить для L12:

В данном случае нельзя утверждать, что L12 равно L21, т.к. величина μ, входящая в формулы, зависит от напряженности H поля в сердечнике.

207

так как ток при этом уменьшается от первоначального значения I до нуля.

Работа, вычисленная по формуле (61.2), идет на нагревание сопротивления R, соленоида и соединительных проводов. Совершение работы сопровож-

дается исчезновением магнитного поля, которое существовало в соленоиде. Так

как никаких других изменений не произошло, можно сделать вывод, что маг-

нитное поле является носителем энергии, за счет которой совершается работа. По закону сохранения энергия магнитного поля:

Выразим энергию магнитного поля через величины, характеризующие само поле. Если соленоид длинный, то его индуктивность

L 0 n2V ,

Напряженность поля внутри соленоида

(см. формулы (59.4) и (50.17)).

Подставим значение L и I в выражение (61.3) и, проведя преобразования, получим:

208

Так как магнитное поле бесконечного соленоида однородно, то энергия распределена по его объему с постоянной плотностью w.

Объемная плотность энергии магнитного поля равна отношению энергии к объему:

Используя соотношение (49.3), можно формуле (61.5) придать вид:

Из формулы (61.6) следует, что носителем энергии является магнитное поле, которое локализовано в пространстве с объемной плотностью w. Объемная плотность энергии пропорциональна квадрату напряженности магнитного поля.

§62 Магнитные измерения

Магнитные измерения это измерения характеристик магнитного поля

или магнитных свойств веществ (материалов). К измеряемым характеристикам магнитного поля относятся: вектор магнитной индукции B , напряженность

магнитного поля H , поток вектора магнитной индукции (магнитный поток) Ф, градиент магнитного поля и др.

Для измерения магнитных характеристик применяют следующие методы:

баллистический, магнетометрический, электродинамический, индукционный,

мостовой, нейтронографический, резонансный и др.

Баллистический метод основан на измерении баллистическим гальвано-

метром количества электричества q, переносимого индукционным током через

надетую на образец измерительную катушку с числом витков N при быстром изменении сцепленного с ней магнитного потока Ф. Изменение магнитного потока

Ф qRN ,

где R сопротивление цепи.

Баллистическим методом определяют основную кривую индукции

B = f(H), кривую намагничивания J = f(H), петлю гистерезиса, различные виды

проницаемости.

Магнетометрический метод основан на воздействии исследуемого намагниченного образца на расположенный вблизи него постоянный магнит. Распространен действующий по этому принципу астатический магнитометр. Он со-

209

Электромагнетизм

стоит из двух одинаковых последовательно включенных в цепь катушек намагничивающей и компенсационной, между которыми на подвесе укреплен магнитный датчик: система из двух линейных магнитов одинаковых размеров с равными магнитными моментами (астатическая система). Магниты расположены параллельно друг другу полюсами в разные стороны. Действие магнитных полей катушек на астатическую систему взаимно компенсировано. Образец, помещаемый в намагничивающую катушку, нарушает скомпенсированность

полей и вызывает поворот системы магнитов. По углу поворота системы опре-

деляют магнитный момент образца. Далее можно вычислить J, B и H. Метод дает возможность найти зависимость B(H) и J(H), петлю гистерезиса и магнитную восприимчивость. Благодаря высокой чувствительности магнитометриче-

ского метода его применяют для измерения геомагнитного поля и решения ряда

метрологических задач.

Иногда для измерения характеристик магнитного поля, в частности в

промышленных условиях, применяется электродинамический метод, при котором измеряется угол поворота рамки с током, находящейся в магнитном поле намагниченного образца. Преимущество метода возможность градуирования шкалы прибора непосредственно в единицах измеряемой величины в Тл

(для B) и А/м (для Н).

Для исследования ферромагнитных веществ в широком интервале значений Н используют индукционный метод, который позволяет измерять B(H), J(H), петлю гистерезиса и различные виды проницаемости. Он основан на из-

мерении эдс индукции, которая возбуждается во вторичной обмотке, намотан-

ной на образец, при пропускании намагничивающего переменного тока через первичную обмотку. Этот метод может быть также использован для измерения намагниченности в сильных импульсных магнитных полях и магнитной вос-

приимчивости диа- и парамагнитных веществ в радиочастотном диапазоне.

Этот метод используется, в частности, в индукционном магнитометре, в котором исследуемый образец колеблется в магнитном поле и при этом возбуждает эдс в измерительных катушках.

Приборы для магнитных измерений классифицируют по их назначению, условиям применения, по принципу действия чувствительного элемента (дат-

чика, или преобразователя). Приборы для измерения напряженности магнитно-

го поля H его индукции B , магнитного момента и ряда других магнитных характеристик вещества обычно называют магнитометрами, из них некоторые имеют свое наименование: для измерения магнитного потока флюксметры или веберметры; потенциала поля магнитные потенциалометры; градиента

градиентометры; коэрцитивной силы коэрцитиметры и т.д.

Индуктивность элементов электрических цепей определят с помощью прибора, который называют измерителем индуктивности (генриметр). Современные генриметры обеспечивают измерение индуктивности в диапазоне 10–8÷105 Гн при погрешности до 0,1%.

210