Вопрос№61

Кроме математического ожидания и дисперсии, для оценки случайной величины используются начальные и центральные моменты случайной величины. Начальным моментом порядка k случайной величины называют математическое ожидание величины :

Центральным моментом порядка k случайной величины X называют математическое ожидание величины: ;

Начальный момент первого порядка равен математическому ожиданию самой случайной величины Х

Центральный момент первого порядка равен нулю:

Центральный момент второго порядка представляет собой дисперсию случайной величины :

Для дискретных случайных величин:

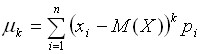
Определение. Математическим ожиданием случайной величины x (иногда применяется термин среднее или генеральное среднее) называется число (другие распространенные обозначения: , равное :

если - дискретная случайная величина и если - непрерывная случайная величина.

Вопрос№62

Пусть  – непрерывная случайная величина. Рассмотрим для некоторого числа х вероятность неравенства х <  < х + х

P(х <  < х + х).

Здесь х – величина малого интервала.

Очевидно, что если х  0, то P(х <  < х + х)  0. Обозначим р(х) предел отношения P(х <  < х + х) к х при х  0, если такой предел существует:

(1)

Функция р(х) называется плотностью распределения случайной величины. Из формулы (1) следует равенство, справедливое для малых величин х, которое также можно считать определением функции р(х):

P(х <  < х + х)  p(x)х (2)

Очевидно, что p(x) – неотрицательная функция. Для определения вероятности того, что случайная величина  примет значение из промежутка [a, b] конечной длины, нужно выбрать на промежутке произвольные числа x₁, х₂,,  х_n удовлетворяющие условию а=х₀<х₁<x₂<<x_n<b=x_n+1. Эти числа разобьют промежуток [a, b] на n+1 частей, представляющих собой промежутки [х₀, х₁), [х₁, х₂), ,[х_n, b]. Введём обозначения:

х₀= х₁ – х₀, х₁= х₂ – х₁, , х_n = b – х_n,

и составим сумму.

Вопрос№63

Вероятность попадания нормальной случайной величины в заданный интервал

Во многих практических задачах требуется определить вероятность попадания случайной величины в заданный интервал. Эта вероятность может быть выражена в виде разности функции распределения вероятности в граничных точках этого интервала:

В случае нормального распределения:

сделаем замену переменной: ,

Тогда:

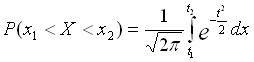
Вероятность попадания в интервал: , , Ф*(Х)=1/2+Ф(Х)

Вопрос№64

У дискретной случайной величины функция распределения ступенчатая.

Вопрос№65

Пусть определено произвольное вероятностное пространство , и случайная величина (или случайный вектор). X индуцирует вероятностную меру называемую распределением случайной величины X.

Определение 3. Если распределение абсолютно непрерывно относительно меры Лебега, то его плотность называется плотностью случайной величины X. Сама случайная величина X называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

Плотность распределения обладает свойствами:

(f1) для любого (f2) ….

Вопрос№66

Пусть непрерывная случайная величина Х задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [a,b]. Математическим ожиданием  непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интегралЕсли возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:Средним квадратичным отклонением называется квадратный корень из дисперсии.Модой М₀ дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным. Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным. Медианой M_D случайной величины Х  называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

Вопрос№67

Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Х^k.Для непрерывной случайной величины: .Начальный момент первого порядка равен математическому ожиданию. Центральным моментом порядка k случайной величины Х называется математическое ожидание величины

Для непрерывной случайной величины: .

Вопрос№68

Математическое ожидание числа есть само число.

M[a] = a — константа;

Математическое ожидание линейно, то есть

M[aX + bY] = aM[X] + bM[Y],

где X,Y — случайные величины с конечным математическим ожиданием, а — произвольные константы;

Математическое ожидание сохраняет неравенства, то есть если почти наверное, и Y — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины X также конечно, и более того

Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если X = Y почти наверное, то

M[X] = M[Y].

Математическое ожидание произведения двух независимых случайных величин X,Y равно произведению их математических ожиданий

M[XY] = M[X]M[Y].