Вопрос№36

Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

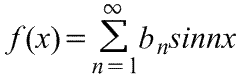
где коэффициенты ряда Фурье,

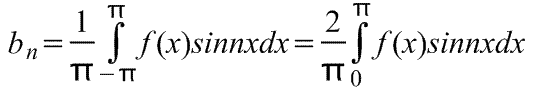
Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

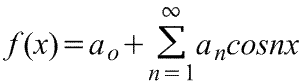
где коэффициенты ряда Фурье,

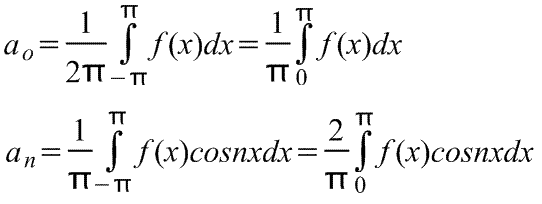
Вопрос№37

Комплексные числа являются расширением множества действительных чисел. В результате расширения множества действительных чисел было введено понятие мнимой единицы , которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:

часто мнимую единицу обозначают через i . Тогда комплексное число z можно представить в виде:

где носит название действительной части или реальной части и обозначается а носит название действительной части или реальной части и обозначается ,а b носит название мнимой части и обозначается как

Операции над комплексными числами

Арифметические операции над комплексными числами были определены в предыдущем пункте. Эти операции обладают следующими свойствами:

1 Коммутативность сложения: z1 + z2 = z2 + z1 для любых Z_1 ,Z₂

2 Ассоциативность сложения: (z1 + z2) + z3 = z1 + (z2 + z3) для любых Z_1 ,Z₂

3 Существует такое число z = 0, которое обладает свойством z + 0 = z для любых Z

4 Для любых двух чисел z1 и z2 существует такое число z, что z1 + z = z2. Такое число z называется разностью двух комплексных чисел и обозначается z = z2 – z1.

5 Коммутативность умножения: z1 z 2 = z 2 z1 для любых Z_1 ,Z₂

6 Ассоциативность умножения: (z1 z2) z3 = z1 (z2 z3) для любых Z_1 ,Z₂ Z ₃

7 Дистрибутивность сложения относительно умножения: z1(z2 + z3) = z1 z2 + z1 z3 для любых Z_1 ,Z₂ Z ₃

8 Для любого комплексного числа z: z · 1 = z.

9 Для любых двух чисел Z₁ N Z₂ существует такое число z , что Такое число z называется частным двух комплексных чисел и обозначается

Деление на ноль невозможно.

Тригонометрическая форма записи комплексных чисел

Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть

и φ = arg z. Тогда по определению аргумента имеем:

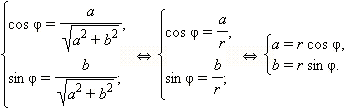
Отсюда получается z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Вопрос№38

Производная комплексной переменной

Определение. Если каждому комплексному числу z

принадлежащему области G

комплексной плоскости (z)

поставлено в соответствие некоторое комплексное число (w),

то говорят, что в области (G)

определена комплексная функция w= f(z)

Множество комплексных чисел {w} соотвествующим всем z э G называется множеством значений функций f (z).

Пусть z= x + iy и w = f(z) . Тогда фнкция w=f(z)

может быть представлена с помощью двух действительных функций U= U(x,y) и V= V(x,y) действительных переменных X и Y:

w=f(z)=u+iy=u(x,y) +iv(x,y),

где: u(x,y) = Ref(z), v(x,y)=Imf(z).

Предел функции компл переменной

Определение. Число w₀ называется предельным значением функции f(x) в точке z₀ если для любого числа e>0 найдется такое число δ>0 что для всех точек z, удовлетворяющих условию

[z –z₀ ]<δ справедливо неравенство

[f(z) – w₀]< e

Непрерывность

Определение. Функция f(z) , заданная на множестве E, называется непрерывной в точке z₀эE если предельное значение этой функции в точке Z₀ существует, конечно и равно частному значению f(Z₀) функции f(z) в точке Z₀ , то есть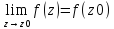

Если функция f(z) , заданная на множестве Е, непрерывна во всех точках этого множества, то говорят, что функция f(z) непрерывна на множестве Е.

Из непрерывности функции комплексной переменной

f(z)=u(x,y) + iv (x,y)

следует непрерывность ее действительной u(x,y) и мнимой v(x,y) частей (по совокупности переменных x и y). Верно и обратное утверждение: если u(x,y) и v(x,y) непрерывные функции переменных x, y в некоторой точке (x₀,y₀) , то функция: f(z)= u(x,y) + iv (x,y)

является функцией комплексной переменной z=x+iy, непрерывной в точке z₀=x₀+iy_0. Это позволяет перенести на функции комплексной переменной основные свойства непрерывных функций двух действительных переменных.

Вопрос№39

Понятие производной вводится для однозначной в D функции

w=f{z).

О: Приращением функции w =f(z) в т. z называется

Производной f(z) функции w =f(z) в т. z называется если предел существует и конечен при любом способе стремления Δz к 0.

Т: Пусть u(х, у), v(x, у) дифференцируемы в т. z. Для того чтобы однозначная функция w =f(z) = u(х, у) + iv(x, у) была дифференцируема в т. z = х + iy, необходимо и достаточно выполнения условий Коши—Римана:

Используя условия Коши—Римана имеем следующие формулы:

Понятие аналитической функции.Правила Диференцирования

аналитичность функции f(z) в области D означает, что она дифференцируема

в каждой точке области D

4.точка z=z₀ является нулем k-го порядка функции f(z) тогда и только тогда,

когда в некоторой

окрестности этой точки функция аналитическая и не равна 0

4.особой точкой функции f(z) называется точка, в которой f(z) не аналитическая

4.функция f(x,y)=u(x,y)+iv(x,y) – однозначно определена и непрерывна в области G,

Г – кусочно-гладкая кривая в области G, тогда равен

если функция f(z) аналитична в некоторой окрестности точки

z₀, а в самой точке z₀ не аналитична, то

точка z₀ называется изолированной особой точкой

Если функции f и g дифференцируемы в точке то в этой же точке дифференцируемы сумма, произведение и частное (если ) этих функций, причем

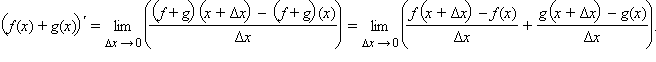
По свойству предела суммы получаем …

Постоянный множитель C можно выносить из-под знака производной:

В частности,