3. Расчёт геометрических размеров колёс

Проектировочный и приближенный расчет главного и основных параметров передач из условия обеспечения изгибной прочности зубьев выполняется для колес с твердостью рабочих поверхностей зубьев более 350 НВ.

z₁ =z3= 16, z2=27

Минимальное значение модуля зацепления для косозубых и шевронных передач:

Выбираем угол наклона зубьев для первой передачи

В приведенную формулу подставляем значения менее прочного элемента (колеса или шестерни) у которого отношение меньше. Для косозубых и, шевронных и конических колесвыбирают по таблице по эквивалентному числу зубьев.

Расчет будем вести по шестерне, так как

K_F – коэффициент нагрузки (предварительно K_F = 1,5);

- коэффициент ширины зуба, принимаем 15;

Коэффициент, который учитывает угол наклона зубьев

Коэффициент, который учитывает участие в зацеплении одновременно несколько пар зубьев:

где -торцевой коэффициент перекрытия

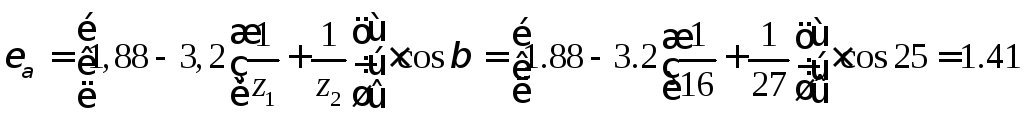
Таким образом

мм

мм

Из стандартного ряда выбираем модуль m=14

Для первой передачи:

Межосевое расстояние

мм

Диаметры окружностей:

делительной:

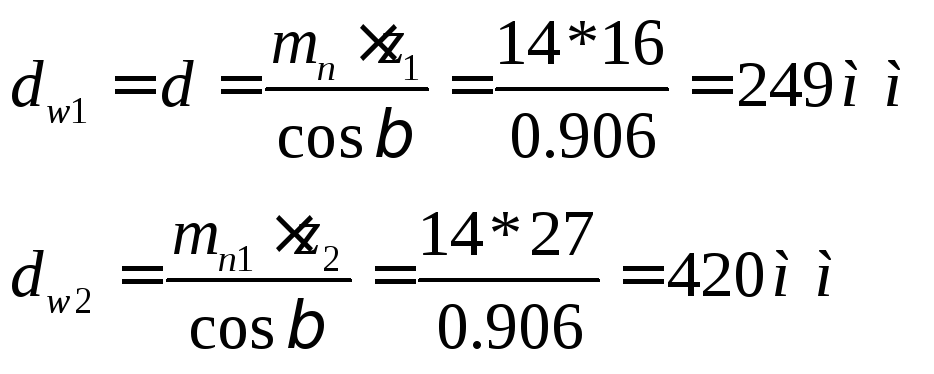
впадин:

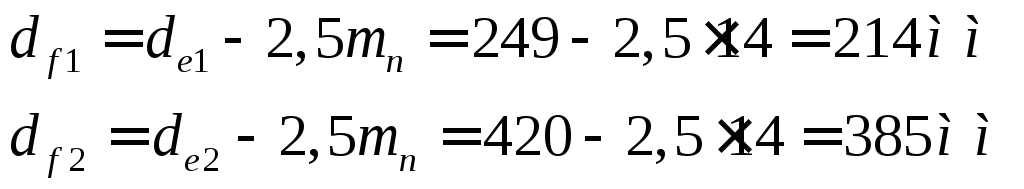
выступов:

Ширина зубчатого венца:

15*14=210мм

мм

Исходя из понятия паразитного редуктора (U=1) принимаем параметры третього колеса идентичные первому.

210мм

Уточним фактический угол наклона зубьев:

Елемент зацепления	Шестерня	Шестерня	Колесо
m, мм	14	14	14
β, град	25	25	25
d, мм	249	420	249
df, мм	214	385	214
da, мм	277	488	277
aω, мм	334	334	334
bω, мм	210	214	210

Определяем ориентировочное значение диаметров валов.

Согласно стандартного ряда d_в1=170 мм, d_в2=210 мм, d_в3=175 мм.

2.4 Назначение степени точности передач

Назначим степень точности изготовления зубчатых передач в зависимости от окружной скорости:

,

.

Принимаем “9” степень точности для обоих передач согласно рекомендациям таблицы 1.11 [2].

2.5 Уточнение расчетной нагрузки

Дополнительные нагрузки учитываются коэффициентом нагрузки при расчете на усталость изгибу k_F, и k_H – при расчете на контактную усталость.

k_F = k_F k_FV и k_H = k_H k_HV

Значение коэффициентов неравномерности распределения нагрузки по ширине венца при расчете на усталость в случае изгиба k_F [2,с.31] ; а при расчете на контактную усталость k_H[2,с.32].

Значение коэффициента динамичности при расчете на усталость изгибу k_FV [2,с.33], а при расчете на контактную усталость k_HV[2,с.34].

k_FV=1.03 k_HV=1.04

k_F=1.04 k_H= 1.04

k_F =1,041,03=1,07 k_H =1,041,04=1,082

2.6 Расчет фактических, изгибающих и контактных напряжений

Фактические напряжения изгиба _F в опасных сечениях основания зубьев шестерен определяем по формуле.

Величина окружного усилия F_t:

Фактические напряжения изгиба в опасных сечениях зуба колеса определяем по упрощенной зависимости:

МПа

МПа

Уточненный расчет фактических контактных напряжений. Фактические контактные напряжения на рабочих поверхностях зубьев _Н определяют по формуле Для цилиндрических передач:

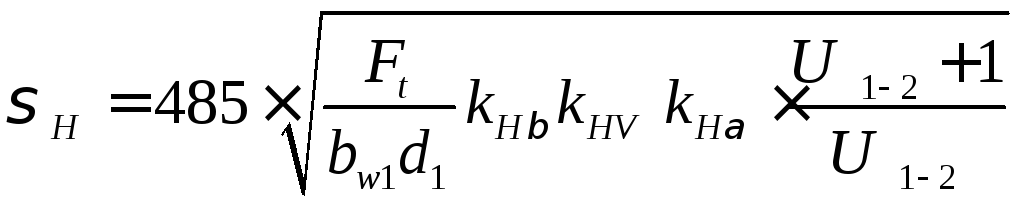
k_H =1,15

МПа