Пример модели простейшей системы
Вероятность
поступления
вызовов
за время
для
закона распределения Пуассона определяется
по следующей формуле:
, (5.1)
где
– интенсивность случайного потока,
т.е. среднее число поступающих заявок
в единицу времени.
Временной
интервал
между
заявками в простейшем потоке подчиняется
экспоненциальному закону распределения:
,
. (5.2)
Предположим,
что длительность обслуживания
заявки
также подчиняется экспоненциальному
закону распределения:
,
, (5.3)
где
– интенсивность обслуживания, т.е.
среднее число обслуженных заявок в
единицу времени.
Рисунок 5.5. – Схема имитационной модели простейшей системы массового обслуживания
5.3 Алгоритм обслуживания заявок
В процессе разработки программы следует придерживаться следующего алгоритма.
Генератор
заявок генерирует некоторый случайным
образом распределенный во времени поток
событий. Система обслуживания с
каналами работает следующим образом:
1-ая заявка поступает на 1-ый канал,
следующая заявка в случае, если занят
1-ый канал – поступает на 2-ой, следующая
заявка поступает на 3-ий, если первые
два канала заняты и т.д. Если все
каналов заняты, то поступившая заявка
получает отказ и формируется файл в
виде случайного потока отказов. Если
освобождается несколько каналов, то
текущая заявка поступает в канал, имеющий
меньший номер. Система обслуживания
обрабатывает заявки, исходя из собственного
времени обслуживания каждого канала и
выдает потоки обслуженных заявок. На
выходе системы должны быть сформированы
файлов в виде случайных потоков
обслуженных заявок.
Порядок выполнения работы
Генератр заявок представляется в виде подпрограммы, генерирующей поток событий, сформированный каждым студентом в 4-ой лабораторной работе.
Время обслуживания текущей заявки
для каждого канала является случайной
величиной и определяется согласно
данных варианта и уравнения (5.3).
Соответствующая подпрограмма, имитирующая
время обслуживания, создается на основе
использования простейшего генератора
случайного события, имеющего Пуассоновское
распределение. Соответствующий алгоритм
приведен в указаниях к выполнению 4-ой
лабораторной работе на рисунке 4.1.Вся система должна функционировать в соответствии с алгоритмом, приведенным в пункте 5.3.
В результате иммитационного моделирования необходимо сформировать
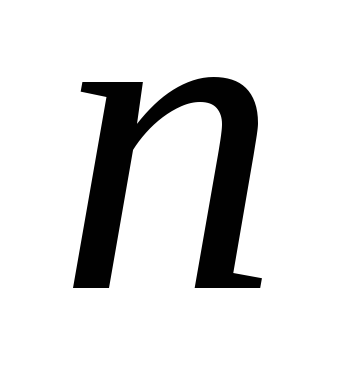файлов для потока обслуживаемых заявок
и 1 файл для потока отказов.Найти количество обслуженных заявок по каждому каналу и количество отказов. Определить среднюю интенсивность обслуженных заявок в единицу времени и интенсивность отказов.
Определить вероятность отказов и вероятность обслуживания для каждого канала по числу отказов и обслуживаний и числу всех событий.
Варианты заданий
|
№ |
Число каналов |
|
|
|
|
|
Приме-чание |
|
1 |
3 |
0,03 |
0,05 |
0,01 |
– |
– |
|
|
2 |
4 |
0,06 |
0,08 |
0,04 |
0,09 |
– |
|
|
3 |
5 |
0,08 |
0,07 |
0,06 |
0,05 |
0,03 |
|
|
4 |
3 |
0,04 |
0,03 |
0,01 |
– |
– |
|
|
5 |
4 |
0,03 |
0,05 |
0,07 |
0,02 |
– |
|
|
6 |
5 |
0,07 |
0,04 |
0,03 |
0,09 |
0,075 |
|
|
7 |
3 |
0,04 |
0,01 |
0,02 |
– |
– |
|
|
8 |
4 |
0,05 |
0,02 |
0,05 |
0,06 |
– |
|
|
9 |
5 |
0,09 |
0,005 |
0,01 |
0,05 |
0,07 |
|
|
10 |
3 |
0,01 |
0,02 |
0,04 |
– |
– |
|
|
11 |
4 |
0,02 |
0,05 |
0,01 |
0,04 |
– |
|
|
12 |
5 |
0,07 |
0,06 |
0,09 |
0,02 |
0,08 |
|
|
13 |
3 |
0,03 |
0,04 |
0,05 |
– |
– |
|
|
14 |
4 |
0,05 |
0,03 |
0,08 |
0,07 |
– |
|
|
15 |
5 |
0,07 |
0,05 |
0,09 |
0,04 |
0,08 |
|
|
16 |
3 |
0,04 |
0,07 |
0,06 |
– |
– |
|
|
17 |
4 |
0,03 |
0,02 |
0,01 |
0,01 |
– |
|
|
18 |
5 |
0,09 |
0,07 |
0,05 |
0,08 |
0,04 |
|
|
19 |
3 |
0,05 |
0,09 |
0,07 |
– |
– |
|
|
20 |
4 |
0,02 |
0,07 |
0,01 |
0,04 |
– |
|
|
21 |
5 |
0,07 |
0,01 |
0,06 |
0,02 |
0,01 |
|
|
22 |
3 |
0,04 |
0,06 |
0,02 |
– |
– |
|
|
23 |
4 |
0,06 |
0,04 |
0,03 |
0,07 |
– |
|
|
24 |
5 |
0,02 |
0,08 |
0,01 |
0,07 |
0,08 |
|
|
25 |
3 |
0,04 |
0,08 |
0,007 |
– |
– |
|
