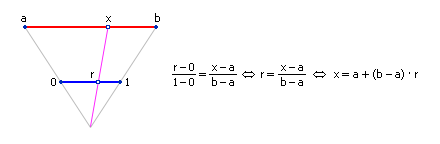- •Министерство образования и науки, молодежи и спорта Украины
- •Лабораторная работа № 1 Определение площади геометрических фигур методом Монте-Карло
- •1.1 Общие положення
- •1.2 Пример нахождения площади круга методом Монте-Карло
- •1.3 Варианты заданий
- •1.3 Контрольные вопросы
- •1.4 Рекомендуемая литература
- •Лабораторная работа № 2 Исследование особенностей и построение моделей сложных объектов и явлений
- •2.1 Порядок выполнения работы
- •2.2 Варианты заданий
- •2.3 Рекомендуемая литература
- •Лабораторная работа №3 Вероятностные модели случайных величин с заданным законом распределения
- •3.1 Общие положения
- •3.1.1 Краткие сведения о распределениях вероятностей случайных величин
- •3.1.2 Источники случайных чисел
- •3.1.3 Детерминированные гпсч
- •3.1.4 Гпсч с источником энтропии или гсч
- •3.2 Порядок выполнения работы
- •3.3. Варианты заданий
- •3.4 Контрольные вопросы
- •3.5 Рекомендуемая литература
- •Лабораторная работа №4 Вероятностные модели случайных потоков событий
- •4.1 Общие положения
- •4.1.2 Простейший (пуассоновский поток)
- •4.1.3 Нестационарный пуассоновский поток
- •4.1.4 Поток Пальма
- •4.1.5 Потоки Эрланга
- •4.2 Создание генераторов потоков случайных событий
- •4.3 Порядок выполнения
- •4.4 Варианты заданий
- •4.5 Контрольные вопросы
- •5.1 Общие положения
- •Пример модели простейшей системы
- •5.3 Алгоритм обслуживания заявок
- •Порядок выполнения работы
- •Варианты заданий
- •5.6 Контрольные вопросы
- •5.7 Рекомендуемая литература
- •Метод генерации нормально распределенных чисел, использующий центральную предельную теорему
- •Метод Мюллера
5.6 Контрольные вопросы
Основные свойства простейшего потока?
Что характеризует параметр
 в экспоненциальном законе распределения?
в экспоненциальном законе распределения?Что характеризует параметр
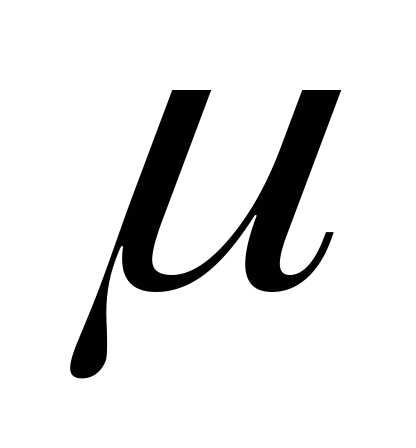 в экспоненциальном законе распределения?
в экспоненциальном законе распределения?Что описывает закон распределения Пуассона?
Что представляет собой последействие в случайном потоке?
Каковы особенности потока Пальма?
Какая величина изменяется случайным образом в случайном потоке: а) на входе сервера (системы обслуживания); б) на выходе сервера?
Что такое пропускная способность СМО?
Что представляет собой производительность источника?
5.7 Рекомендуемая литература
Е.С. Вентцель Теория вероятностей: учебник для втузов / Е.С. Вентцель. 8-е изд., перераб. и доп. – М. : Физматлит, 1999. – 576 с.
Моделирование информационных систем: уч. пос. /ред. О.И. Шелухина. – М.: Радиотехника, 2005. – 368 с.
Приложение А. – Основные сведения по генераторам случайных чисел
В
основе метода Монте-Карло лежит генерация
случайных чисел, которые должны быть
равномерно распределены в интервале
![]() .
.
Если генератор выдает числа, смещенные в какую-то часть интервала (одни числа выпадают чаще других), то результат решения задачи, решаемой статистическим методом, может оказаться неверным. Поэтому проблема использования хорошего генератора действительно случайных и действительно равномерно распределенных чисел стоит очень остро.
Математическое
ожидание
![]() и дисперсия
и дисперсия![]() такой последовательности, состоящей
из
такой последовательности, состоящей
из![]() случайных чисел
случайных чисел![]() ,
должны быть следующими (если это
действительно равномерно распределенные
случайные числа в интервале от 0 до 1):
,
должны быть следующими (если это
действительно равномерно распределенные
случайные числа в интервале от 0 до 1):
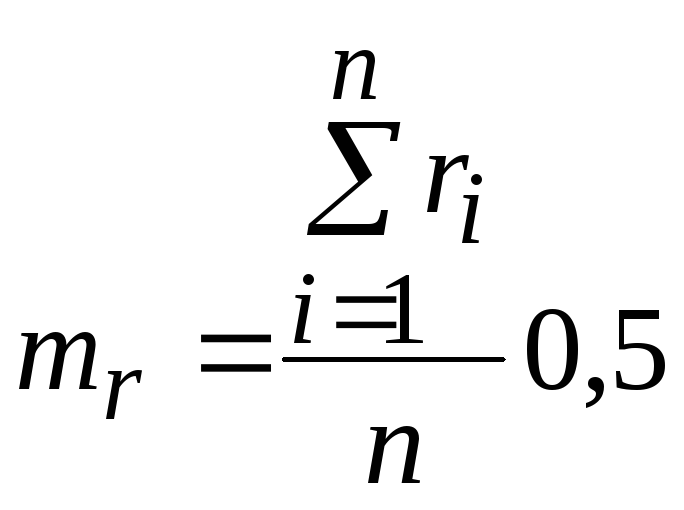 ,
,
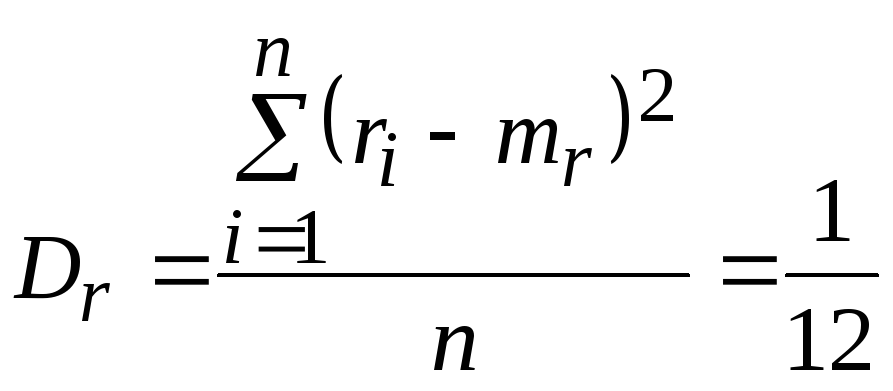 .
.
Если
пользователю потребуется, чтобы случайное
число x
находилось в интервале
![]() ,
отличном от
,
отличном от![]() ,
нужно воспользоваться формулой
,
нужно воспользоваться формулой![]() ,
где
,
где![]() – случайное число из интервала
– случайное число из интервала![]() .
Законность данного преобразования
демонстрируется на
рисунке
А.1.
.
Законность данного преобразования
демонстрируется на
рисунке
А.1.
|
|
Рис.
А.1. Схема перевода числа из интервала
![]() в
интервал
в
интервал
![]()
Теперь
![]() – случайное число, равномерно
распределенное в диапазоне от
– случайное число, равномерно
распределенное в диапазоне от![]() до
до![]() .
.
За
эталон генератора
случайных чисел
(ГСЧ) принят такой генератор, который
порождает последовательность
случайных чисел с равномерным
законом распределения в интервале
![]() .
За одно обращение данный генератор
возвращает одно случайное число. Если
наблюдать такой ГСЧ достаточно длительное
время, то окажется, что, например, в
каждый из десяти интервалов
.
За одно обращение данный генератор
возвращает одно случайное число. Если
наблюдать такой ГСЧ достаточно длительное
время, то окажется, что, например, в
каждый из десяти интервалов![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() попадет практически одинаковое количество
случайных чисел – то есть они будут
распределены равномерно по всему
интервалу
попадет практически одинаковое количество
случайных чисел – то есть они будут
распределены равномерно по всему
интервалу![]() .
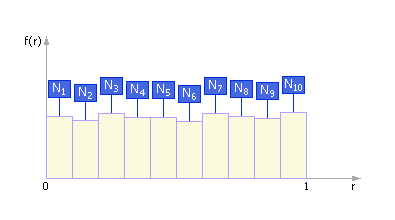
Если изобразить на графике
.
Если изобразить на графике![]() интервалов и частоты
интервалов и частоты![]() попаданий в них, то получится
экспериментальная кривая плотности
распределения случайных чисел (см.рис.
А.2).
попаданий в них, то получится
экспериментальная кривая плотности
распределения случайных чисел (см.рис.
А.2).
|
|
Рис. А.2. Частотная диаграмма выпадения случайных чисел, порождаемых реальным генератором
Заметим,
что в идеале кривая плотности распределения
случайных чисел выглядела бы так, как
показано на
рисунке
А.3.
То есть в идеальном случае в каждый
интервал попадает одинаковое число
точек:
![]() ,
где
,
где![]() – общее число точек,
– общее число точек,![]() – количество интервалов,
– количество интервалов,![]() .
.
Функциональные преобразования для имитации случайных процессов
Случайные процессы имитируются в основном с использованием равномернораспределенного генератора случайных чисел.
Нормальное распределение моделируется следующими способами.
Табличный метод генерации нормально распределенных чисел
Для
этого
нормальное число можно взять из
справочника в таблице функции Лапласа
и получить случайное число по методу
взятия обратной функции:
![]() ,
где
,
где![]() – интегральная функция Лапласа.
– интегральная функция Лапласа.
Технически
это означает, что надо разыграть случайное
равномерно распределенное число
![]() из интервала
[0; 1] стандартным
ГСЧ, найти равное ему число в
таблице
значений функции Лапласа
в столбце F
и по строке определить случайную величину
из интервала
[0; 1] стандартным
ГСЧ, найти равное ему число в
таблице
значений функции Лапласа
в столбце F
и по строке определить случайную величину
![]() ,
соответствующую этому числу.
,
соответствующую этому числу.
Недостатком метода является необходимость хранения в памяти компьютера всей таблицы чисел функции Лапласа.