glava04
.pdf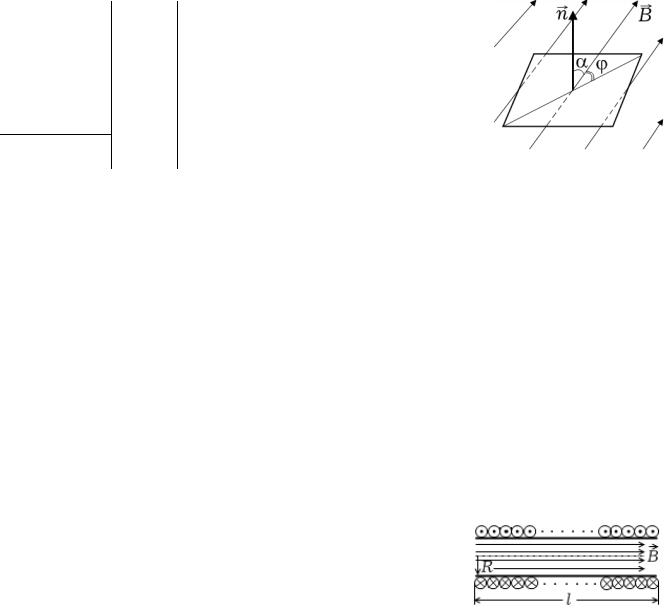
Решение
Поток вектора магнитной индукции через поверхность ограниченную контуром определяется по формуле
Φ = BS cos α ,
где S = a2 – площадь поверхности контура, α = 90°−ϕ – угол между нормалью к поверхности контура и направлением силовых линий магнитного поля. С учетом этого формула для магнитного потока имеет вид
F= Ba2 cos(90° - j) = Ba2 sin j .
Вполученное выражение подставим числовые значения
F= 0,02 Тл×(0,05 м)2 ×sin 30° = 2,5 ×10−5 Вб = 25 мкВб .
Задача 2. Найдите магнитный поток, пронизывающий поперечное сечение длинного соленоида, если ток в нем 1 А, плотность намотки 25 витков/см, а ради-
ус соленоида 10 см. |
|
|
|
|
|
Дано: |
СИ |
Решение |
I =1 А |
|
Магнитный поток, |
n = 25 витков/см |
2500 витков/м |
пронизывающий |
R =10 см |
0,1 м |
поперечное сечение соленоида определяется |
|
|
|
Φ = ? |
|
по формуле |
|
|
|
Φ = BS ,
где S = pR2 – площадь поперечного сечения соленоида; B индукция магнитного поля внутри соленоида, которая определяется по формуле
B = μ0NI . l
Учитывая, что плотность намотки витков определяется выражением n = N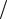
l , для магнитного потока получаем следующее равенство
Φ = μ0πR2nI .
Подставим числовые значения
F = 4 ×3,14 ×10−7 Гн/м×3,14 ×(0,1 м)2 × 2500 витков/м×1 А » 10−4 Вб = 100 мкВб.
§ 44
Работа по перемещению проводника и контура с током в магнитном поле
Определим работу, которую совершает магнитное поле по перемещению не закрепленного проводника с током. По закону Ампера на проводник действует сила равная
F = IBl .
Под действием этой силы проводник перемещается из точки 1 в точку 2 на отрезок dx.
Магнитное поле совершает работу равную
dA = Fdx = IBldx = IBdS = IdΦ .
Таким образом, |
|
dA = IdΦ . |
(44.1) |
Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
Вычислим работу по перемещению замкну-
того контура с постоянным током в магнитном
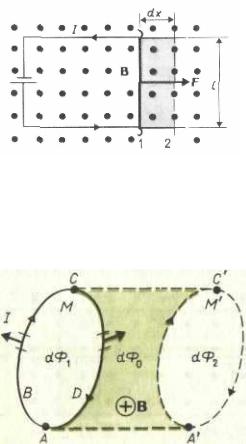
поле. Контур M разобьем мысленно на два соединенных своими концами провод-
ника: ABC и CDA. Работа совершаемая силой Ампера по перемещению контура в магнитном поле равна
dA = dA1 + dA2 , |
(44.2) |
где dA1 – работа по перемещению проводника ABC, dA2 – |
работа по перемеще- |
нию проводника DCA. |
|
Силы, приложенные к проводнику CDA, образуют острый угол с направле-
нием перемещения и, следовательно, dA2 > 0 . Тогда согласно формуле (44.1):
dA2 |
= I(dΦ0 + dΦ 2 ) , |
(44.3) |
|
где dΦ0 – |
поток сквозь поверхность, находящуюся между начальным и конеч- |
||
ным положением конура; dΦ 2 – |
поток сквозь контур в его конечном положении. |
||
Силы, действующие на участок ABC, образуют с направлением перемеще- |
|||
ния тупой угол dA1 |
< 0 : |
|
|
dA1 = −I(dΦ 0 |
+ dΦ1 ), |
(44.4) |
|
где dΦ1 – |
поток через поверхность контура в первоначальном положении. |
||
Подставляя (44.3) и (44.4) в (44.2), получим выражение для элементарной работы:
dA = I(dΦ 2 − dΦ1 ),
где dФ2 −dΦ1 = dΦ′ – |
изменение магнитного потока через площадь, ограничен- |
ную контуром с током. |
|
dA = IdΦ′ . |
(44.5) |
Проинтегрировав (44.5), получим выражение для работы силы Ампера при про-
извольном конечном перемещении
A = IΔΦ . |
(44.6) |
Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.
Задача 1. В однородном магнитном поле с индукцией 0,05 Тл перпендику-
лярно линиям поля движется равномерно провод длиной 20 см со скоростью 10
м/с. По проводу течет ток силой 1 A. Найдите работу по перемещению провода за время 20 с.
Дано: |
СИ |
Решение |
B = 0,05 Тл |
|
На проводник с током в магнитном поле, как показа- |
l = 20 см |
0,2 м |
но на рисунке, действует сила Ампера, направление кото- |
v =10 м/с |
|
рой определяется по правилу левой руки, а ее величина – по |
I = 1 А |
|
формуле |
t = 20 с |
|
F = IBl . |
|
|
При перемещении проводника из положения 1 в положение |
A = ? |
|
|
|
|
2 магнитное поле совершает элементарную работу |
|
|
dA = Fdx = IBldx ,
где dx = vdt – перемещение проводника за промежуток времени dt . С учетом этого работа равна
dA = IBlvdt .
Тогда работа, совершенная полем за промежуток времени t , будет равна
t |
t |
t |
A = ∫dA = ∫IBlvdt = IBlv∫dt = IBlvt . |
||
0 |
0 |
0 |
Подставим числовые значения в полученное выражение для работы поля
A = 1 А×0,05 Тл×0,2 м×10 м/с× 20 с = 2 Дж .
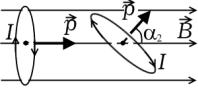
Задача 2. Виток радиусом 10 см, по которому течет ток 1 A, свободно уста-
новился в однородном магнитном поле с индукцией 0,1 Тл. Виток повернули от-
носительно диаметра на угол 45°. Определите совершенную при этом механиче-
скую работу. |
|
|
|
||
Дано: |
|
СИ |
|
Решение |
|
|
|
||||
R = 10 см |
|
0,1 м |
|
При повороте витка с током в |
|
I = 1 А |
|
|
|
магнитном поле |
внешние силы |
B = 0,1 Тл |
|
|
|
совершают механическую работу, которая равна работе поля |
|
α1 = 0° |
|
|
|
со знаком минус, т.е |
|
α2 = 45° |
|
|
|
A = -IDF , |
|
|
|
|
|
где ΔΦ = Φ2 −Φ1 – |
изменение магнитного потока через |
A = ? |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
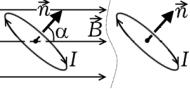
поверхность, ограниченную витком; Φ1 = BS cos α1 – магнитный поток пронизы-
вающий эту поверхность до поворота витка и Φ2 = BS cos α2 – магнитный поток после поворота витка; S = pR2 – площадь поверхности, ограниченной витком.
Подставив все величины в формулу для работы, получим
A= -I(F2 - F1 ) = IBS(cos a1 - cos a2 ) = pIBR2 (cos a1 - cos a2 ) .
Вполученное выражение подставим числовые значения
A= 3,14 ×1 А×0,1 Тл×(0,1 м)2 ×(cos 0° - cos 45°) » 9,2 ×10−4 Дж = 920 мкДж .
Задача 3. Виток радиусом 5 см с током 2 А помещен в магнитное поле с индукцией 0,1 Тл так, что нормаль к витку составляет угол 60° с линиями поля.
Найдите работу, которую надо совершить, чтобы удалить виток из поля.
Дано: |
СИ |
Решение |
R = 5 см |
0,05 м |
При удалении витка с током |
I = 2 А |
|
из магнитном поле внешние силы |
α = 60° |
|
совершают механическую работу, которая равна |
B1 = 0,1 Тл |
|
A = −IΔΦ, |
B = 0 |
|
где ΔΦ = Φ2 −Φ1 – изменение магнитного потока через по- |
2 |
|
|
|
|
верхность, ограниченную витком. Так как виток удаляют за |
A = ? |
|
|
|
|
пределы магнитного поля, то магнитный поток Φ2 = 0 . Вна- |
|
|
чале поток вектора магнитной индукции через поверхность ограниченную витком был равен
Φ1 = B1Scos α ,
где S = pR2 – площадь поверхности, ограниченной витком. С учетом этого вы-
ражение для работы будет иметь вид
A = IF1 = IB1Scos a = pIB1R2 cos a .
Подставим в полученную формулу числовые значения
A = 3,14 × 2 А×0,1 Тл×(0,05 м)2 ×cos 60° » 7,85 ×10−4 Дж = 785 мкДж .